位置和姿态的相对位姿描述

1.刚体立姿

刚体位置与姿态表示物体在环境中的位置和方向，如工业机器人末端工具相对于法兰盘的位姿，而位姿描述的物体包括机器人工具、摄像机、工件、障碍物等。图7.1所示为工具具有相同位置，但方向各不同；图7.2所示为工具坐标系和法兰坐标系之间的关系。

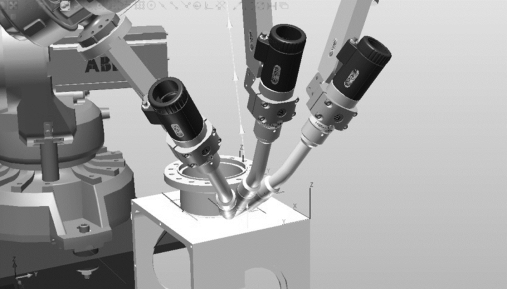
图7.1　工具具有相同位置，但方向不同

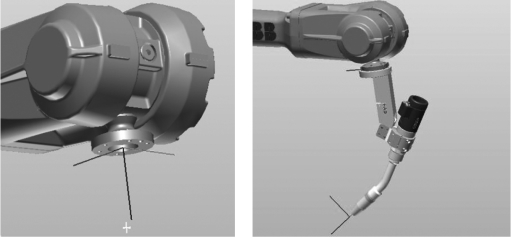
图7.2　工具坐标系和法兰坐标系之间的关系

2.点的位置向量

空间中的点是数学中一个熟悉的概念，它可以被描述为一个坐标向量，也被称为一个约束向量，如图7.3（a）所示。坐标向量表示点相对于某个参考坐标系的位移。一个坐标系是由一组正交轴构成的，这些轴相交于一个被称为原点的点。

假设物体是刚性的，则可认为：组成物体的一组点相对于物体坐标系保持固定的相对位置，如图7.3（b）所示。表示物体位置和方向时并不是描述其上单独的点，而是用该物体坐标系的位置和方向来描述。物体坐标系的标记形如{B}，其坐标轴为xB、yB 。图7.3（a）中点P 由一个相对于绝对坐标系的坐标向量表示。图7.3（b）这些点是用相对于物体坐标系{B}坐标向量表示。

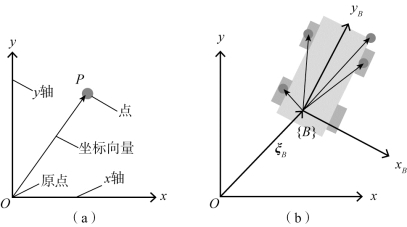
图7.3　位姿描述的示意

3.相对位姿

坐标系的位置和方向总称为位姿，用符号ξ 表示，即一个坐标系相对于另一个参考坐标系的相对位姿。图7.4（a）显示了两个坐标系{A}、{B}，以及{B}相对于{A}的相对位姿AξB 。在AξB 中前面的上标表示参考坐标系，下标表示被描述的坐标系。AξB 描述了对{A}施加平移和旋转，使它转化为{B}的一组动作。如果没有初始上标，默认位姿的变化是相对于用{O}表示的世界坐标系的，即绝对坐标。

4.点在不同坐标系下的转换

在图7.4（a）中的点P 可用任何一个坐标系表示。用公式表示为

上式中等号右侧表示从{A}到{B}，然后到P 的动作。运算符“·”将一个向量转换为一个新的向量，它们是用一个不同的坐标系来描述的相同点。

5.相对位姿合成

相对位姿的一个重要特点是它们可以被合成。如图7.4（b）所示，如果一个坐标系可以被其他坐标系用相对位姿描述，那么它们的关系可以记为

上式可以表述为{C}相对于{A}的位姿可由{B}相对于{A}的位姿和{C}相对于{B}的位姿合成得到。利用运算符“⊕”表示相对位姿的合成。

图7.4（a）中点P 既可以用相对于坐标系{A}的坐标向量表示，又可以用相对于坐标系{B}的坐标向量表示。坐标系{B}相对于坐标系{A}的位姿记作AξB。

图7.4（b）中点P 可以用相对于坐标系{A}、{B}或{C}的坐标向量表示。这些坐标系用相对位姿描述，在这种情况下，点P 可被表示为

(www.xing528.com)

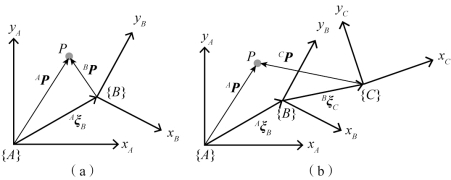
图7.4　位姿描述示意

6.位姿的代数运算

（1）用图表示相对位姿。有向图是另一个表示空间关系的方式，如图7.5所示。图中的每个节点都代表一个位姿，每条边代表一个相对位姿。从X 到Y 的箭头记作XξY，表示Y相对于X 的位姿。用运算符⊕来复合成相对位姿，则图7.5 中的空间关系为

式（7.4）中的每个方程表示了图中的一个闭环。方程等号两侧的每一边各表示一条网络的通路，即一组按照从头到尾顺序连接的边（箭头线）。等式两边的起始节点和结束节点必须相同。

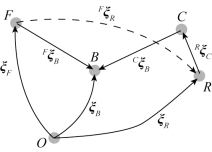
图7.5　有向图的空间关系表示示例

（2）位姿代数运算规则如下：

①0（零位姿）表示一个零相对位姿，它的代数运算规则为

ξ ⊕0= ξ,ξ⊙0= ξ

ξ⊙ξ= 0,⊖ξ ⊕ξ= 0

②一个位姿的逆位姿为

⊙XξY=YξX

③相对位姿复合为

XξY ⊕YξZ=XξZ

总结如下：

（1）一个点用坐标向量来表示其位置。（点的向量表示）

（2）一个刚体可以用单独一个坐标系描述。（刚体的坐标表示）

（3）一个物体在坐标系中的位置和方向称为它的位姿。（物体位姿）

（4）一个相对位姿表示一个坐标系相对于另一个坐标系的位姿，记作ξ。（相对位姿）

（5）一个点可以用不同坐标系中的不同坐标向量来描述，坐标向量之间通过坐标系相对位姿来转换，其运算符为“·”。（点的变换）

（6）用相对位姿写成的代数表达式是可以进行代数运算的。（坐标的变换）