同一截面对于不同坐标轴的惯性矩和惯性积虽然各不相同，但当其中一对坐标轴是平面图形的形心轴时，它们之间都存在着一定的关系。这些关系可以使计算简化，有助于应用简单平面图形的结果来计算组合平面图形的惯性矩和惯性积，有助于计算截面对于某些特殊轴的惯性矩和惯性积。本节将介绍当坐标轴转换时，截面对于两对不同坐标轴的惯性矩和惯性积之间的关系。
图A.10
A.3.1 平行移轴公式
任意平面图形如图A.10所示，C为图形的形心，zc轴、yc轴是平面图形的形心轴。平面图形对于该两轴的惯性矩和惯性积分别为
选取另一分别与zc轴、yc轴平行的坐标系yOz，它们之间的距离分别为a和b如图A.10所示，满足关系
图形对y轴的惯性矩为
由于平面图形对于形心轴的静矩恒等于零，即
故有
Iy＝Iyc＋b2 A
同理可得 Iz＝Izc＋a2A和Iyz＝Iyczc＋abA
因此称表达式
为惯性矩和惯性积的平行移轴公式。表明：
（1）平面图形对于任一轴的惯性矩，等于平面图形对于与该轴平行的形心轴的惯性矩加上截面的面积与两轴距离平方的乘积。
（2）平面图形对于任意两轴的惯性积，等于平面图形对于与该两轴平行的形心轴的惯性积加上平面图形的面积与两对平行轴间距离的乘积。
（3）图形对一簇平行轴的惯性矩中，以对形心轴的惯性矩为最小。另外，公式中的a和b是形心C在y Oz坐标系中的坐标，可为正，也可为负；公式中Iyc、Izc和Iyczc为图形对形心轴的惯性矩和惯性积，即zc、yc轴必须通过截面的形心，对于这两点，在具体使用公式时应加以注意。
A.3.2 组合图形的惯性矩和惯性积
在工程实际中常会遇到组合图形，计算其惯性矩和惯性积需用到公式（A.10），而此式中Izi、Iyi、Iyzi的计算常会用到平行移轴公式（A.11），对此下面将用例题来加以说明。
【例A.6】 试求图A.11所示图形对其形心轴的惯性矩和惯性积。
解：将图形看成是两个矩形Ⅰ、Ⅱ的组合，取其对称轴为z轴，其与另一垂直轴y＇轴组成参考坐标系。
（1）确定形心的位置。
（2）求图形对z轴的惯性矩。(www.xing528.com)
（3）求图形对y轴的惯性矩。
a1＝150－103.3＝46.7（mm）
a2＝103.3－70＝33.3（mm）
Iy＝Iy1＋Iy2＝443×104＋768×104＝1211×104（mm4）
（4）求图形对y、z轴的惯性积。因为z轴是对称轴，故Iyz＝0。
【例A.7】 图A.12所示截面，由2个20号槽钢用缀板连接而成，试求此组合截面分别对形心轴y、z轴的惯性矩，图中尺寸单位为cm。
图A.11
图A.12
解：先把20号槽钢的有关数据从附录中的型钢表中查出。
槽钢形心到腹板边缘的距离为1.95cm，槽钢面积A1＝A2＝32.83cm2
槽钢对各自形心轴的惯性矩为
Iyc1＝Iyc2＝1913.7cm4
Izc1＝Izc2＝143.6cm4
（1）计算截面对y轴的惯性矩。
Iy＝Iyc1＋Iyc2＝1913.7＋1913.7＝3827.4cm4
（2）计算截面对z轴的惯性矩。两槽钢的形心轴zc1和zc2与z轴之间的距离为
b1＝b2＝CC1＝1.95＋2.5＝4.45（cm）
于是
Iz＝Izc1＋A1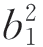
＋Izc2＋A2
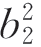＝2×（143.6＋32.82×4.452）＝1587.4（cm4）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
