安全系数法：保障工业安全的有效途径

对于压杆来说，当其横截面上的正应力达到临界应力时，压杆就要失稳。因此，正常工作的压杆，其横截面上的正应力应小于临界应力。为了保证压杆具有足够的稳定性，还必须考虑有一定的安全储备。因此，在对压杆进行稳定计算时，以临界应力除以大于1的安全系数所得的数值为准，即要求横截面上的正应力，通常将稳定条件写成下列用安全系数表达的形式：

式中：nst为规定稳定安全系数，n称为压杆的工作安全系数。

由于实际压杆初始缺陷的存在，严重的影响压杆的稳定，导致压杆的稳定性降低，同样这些因素也对压杆的强度有影响，但影响强度的程度远不如影响稳定性严重，因此稳定安全系数nst一般应高于强度全系数，nst可从相应的设计规范或设计手册中查到。几种常见压杆的稳定安全系数见表7.2。

表7.2　几种常见压杆的稳定安全系数

图7.7

【例7.5】 图7.7所示结构中，梁AB为No14普通热轧工字钢，支柱CD的直径d＝20mm，二者的材料均为A3钢，结构的受力及尺寸如图所示，A、C、D三处均为球铰约束，材料的弹性模量E＝200GPa，梁的许用应力[σ]＝160MPa，规定稳定安全系数nst＝2，试校核此结构是否安全。

解：此结构中AB梁承受拉伸与弯曲的组合变形，属于强度问题，支承杆CD承受压力，属于稳定性问题，应分别校核。

（1）AB梁的强度校核。梁在C处弯矩最大，故为危险截面，其弯矩和轴力分别为

Mmax＝20×sin30°×1.25＝12.5（k N·m）

FNmax＝20×cos30°＝17.32（k N）(www.xing528.com)

由型钢表查得No14普通热轧钢的抗弯截面系数和面积分别为

Wz＝102×10－6 m3，A＝21.5×10－4 m2

由叠加法可求得AB梁的最大正应力为

故梁AB满足强度要求。

（2）压杆CD的稳定校核。由平衡条件求得压杆CD的轴力为

FNCD＝2×20×sin30°＝20k N

由于是圆截面杆，则，再由压杆CD两端为球铰约束，所以u＝1，压杆CD的柔度为

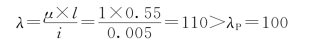
表明压杆CD为大柔度杆，可采用欧拉公式计算临界荷载

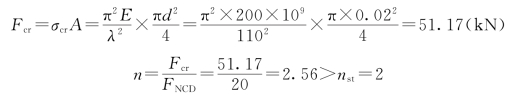
故CD压杆满足稳定性要求。