偏心拉压应力计算方法

杆件受到平行于轴线但不与轴线重合的力作用时[图6.16（a）]，引起的变形称为偏心拉伸（压缩）。图6.2所示为装有吊车的厂房柱。

现以图6.16（a）所示矩形截面杆在A点受拉力F作用的情况为例来说明应力的计算。设力F作用点的坐标为yF和zF。现将力F简化到截面的形心O，于是得到轴力F和两个弯矩My、Mz，从而引起轴向拉伸和两个平面弯曲的组合[图6.16（b）]，其中两个弯矩分别为

它们引起的正应力分别为

图6.16

轴力F引起的正应力为

在上述各式中，F为拉力时取正，压力时取负；弯矩My和Mz的正负号这样规定：使截面上位于第一象限的各点产生拉应力者为正，产生压应力者为负。在图6.16（b）中所示的My和Mz均为正。

相应的应力分布情况绘于图6.17，其中图6.17（a）为式（6.26）所表达的情况，图6.17（b）、（c）分别为式（6.24）和式（6.25）所表达的情况。

将上述三项应力代数相加即得偏心拉伸（压缩）的总应力：

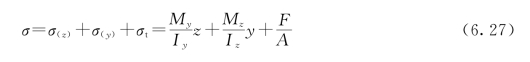
或

其应力分布图示于图6.17（d）。

图6.17

现来讨论偏心拉伸（压缩）时的应力分布规律。将式（6.27a）改写成

再利用关系

式中：iy和iz称为截面面积对y轴和z轴的惯性半径，则式（6.28）写成

此式表明应力是y和z的一次函数，即其分布规律是一个平面。此平面与坐标zy平面的交线为一条直线，其上应力等于零，称为中性轴。令中性轴上任一点的坐标为y0、z0，则将它们代入式（6.30）得到的应力都应等于零，即(www.xing528.com)

由此得中性轴的方程为

此方程表明，中性轴是一条不通过坐标原点（截面形心）的直线。欲确定它的位置，可求出它在两坐标轴上的截距。

分别令上式中的y0＝0、z0＝0，得直线在z轴和y轴上的截距为

图6.18

式（6.33）等号右边的负值表明，若力F作用点的坐标yF和zF均为正号时，则中性轴的两个截距都是负的，即中性轴与力作用点必分别处于截面形心的两侧。

中性轴把截面划分为拉应力和压应力两个区域，一旦中性轴的位置确定，就很容易确定危险点的位置，只要选取离中性轴最远的点就是。其中一个是最大拉应力作用点，一个是最大压应力作用点，如图6.18中的D1和D2点。

把危险点的坐标代入式（6.27）或式（6.28）即可求得最大应力。选取其中绝对值最大的应力作为强度计算的依据。强度条件为

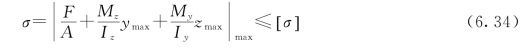
或

若材料的许用拉应力[σ]t和许用压应力[σ]c不等时，则须分别对最大拉应力和最大压应力作强度计算。

【例6.3】 图6.19（a）示一矩形截面混凝土短柱，受偏心压力F的作用，作用点在y轴上，偏心距为yF[图6.19（c）]。已知：F＝100k N，yF＝40mm，h＝120mm，b＝200mm。试求任一截面m—n上的应力。

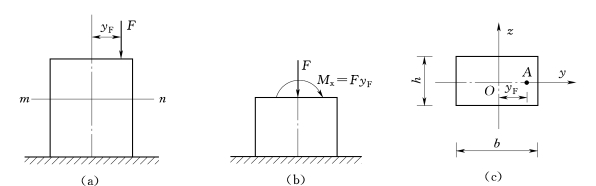
图6.19

解：将力F简化到截面形心O[图6.19（b）、（c）]，得轴力F和弯矩Mz＝FyF，应用式（6.27）

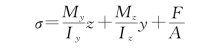
对于此例

F＝－100k N，Mz＝FyF＝－100×103 N×40×10－3 m＝－4000N·m

My＝0，A＝b·h＝200×120×10－6 m2＝24000×10－6 m2

最大应力发生在截面的左右边界上，该处。将上述数据代入式（6.27），得