变形分析与应力分析 - 工字钢22b在危险截面的最大应力分析

斜弯曲的变形计算也可采用叠加法。仍以图6.4所示的悬臂梁为例，设要求自由端的挠度为f。方法是先分别求出两个平面弯曲的挠度，如y方向的挠度fy为

z方向的挠度fz为

总挠度f为上述两个挠度的几何和（图6.10），其大小为

将式（6.13）和式（6.14）的值代入式（6.15），即可求得f值。

至于总挠度f的方向，若设f与y轴的夹角为β（图6.10），则有

式（6.16）表明，总挠度方向与力F方向不一致，即荷载平面不与挠曲线平面重合（图6.9），这正是斜弯曲的特点。除非截面的两个形心主惯性矩Iz＝Iy。此时β＝φ，荷载平面与挠曲线平面重合，而这就是平面弯曲了。

图6.9

图6.10

【例6.1】 图6.11所示一工字型钢简支梁，跨中受集中力F作用。设工字钢的型号为22b。已知F＝20k N，E＝2.0×105 MPa，φ＝15°，l＝4m。试求：

（1）危险截面上的最大正应力。

（2）最大挠度及其方向。

解：（1）计算最大正应力σmax。先把荷载沿z轴和y轴分解为两个分量

Fz＝F sinφ，Fy＝F cosφ

图6.11

危险截面在跨中，其最大弯矩分别为

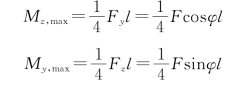(www.xing528.com)

根据上述两个弯矩的转向，可知最大应力发生在D1和D2两点（图6.11b），其中D1为最大拉应力的作用点，D2为最大压应力的作用点。两点应力的绝对值相等，所以计算一点即可，例如计算D2点：

由型钢表查得Wz＝325cm3，Wy＝42.7cm3，代入上式，得

（2）计算最大挠度f及其方向。先分别算出沿z轴和y轴方向的挠度分量，即

根据式（6.15），总挠度为

由型钢表查得Iz＝3570cm4，Iy＝239cm4，代入上式，得

设总挠度f与y轴的夹角为β[图6.11（c）]，则根据式（6.16）有

所以β＝76°

（3）作为比较，设力F的方向与y轴重合，即发生的是绕z轴的平面弯曲，试求此情况下的最大正应力σmax和最大挠度f。

此时，D1和D2两点的应力仍是最大的，其值为

将斜弯曲时的最大应力与此应力比较，得

最大挠度f°为

将斜弯曲时的最大挠度f与此f°比较，得

上述比较可见当Iz较Iy大得多时，力的作用方向与主惯性轴稍有偏离，则最大应力和最大挠度将比没有偏离时的平面弯曲的增大很多。例如本例力F仅偏离15°，而最大应力和最大挠度分别为平面弯曲时的3倍和4倍，所以对于两个主惯性矩相差较大的梁，应尽量避免斜弯曲的发生。