莫尔强度理论的原理及应用解析

莫尔强度理论是在最大切应力理论基础上发展起来的一个理论。德国工程师莫尔（O.Mohr）1882年提出应力圆方法后的18年，将特雷斯卡（H.Tresca）的最大切应力理论加以推广，并应用他本人早先提出的应力圆方法建立了强度条件。莫尔在工程实践中积累了丰富的经验，莫尔强度理论是建立在试验的基础之上的。

1.莫尔强度理论的基本观点

（1）摩擦力的影响。莫尔认为材料的剪切破坏不一定沿着最大切应力所在的截面滑移破坏，因为滑移面上除τmax外还有正应力。当两个面相对滑移时，面与面之间就产生摩擦力，根据理论力学知识我们知道，这个摩擦力F不仅与材料性质有关，还与正压力N有关。

（2）极限应力圆和包络线。根据三向应力圆的性质，切应力和最大（最小）正应力的变化范围都不超出由σ1和σ3作出的最大应力圆，且最大切应力、最大和最小正应力σ1和σ3都在这个圆上。若把某一材料做成一组试样，在不同的主应力比值下进行破坏试验每一个试样可得一个应力圆。

材料破坏时的最大应力圆称为极限应力圆。一组试样就能得到圆心在σ坐标轴上的一组极限应力圆。画这组应力圆的包络线，称为该材料的极限曲线。各种材料都可以通过试验得出它的极限曲线。

（3）最大工作应力圆和破坏应力及其所在截面。用某一材料制成的实际受力构件，将其危险点的应力状态画出最大应力圆，称为最大工作应力圆。若此工作应力圆在极限应力圆的包络线之内，则表示此应力圆所代表的应力状态不会引起材料的破坏。若此工作应力圆与包络线相切，就表示此应力圆所代表的应力状态将引起材料的破坏。

2.莫尔强度理论的简化

如果采用许多试样在各种应力状态下进行试验，作极限应力圆画出包络线，是非常困难的。为了应用的方便，通常进行简化。从而得到莫尔理论的强度条件为

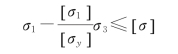
上式不等号左边就是莫尔强度理论的相当应力。[σ1]、[σy]分别为材料的许用抗拉应力和许用抗压应力。

当材料抗拉应力和抗压应力相等时，[σ1]＝[σy]时，此时的莫尔强度理论变成：

σ1－σ3≤[σ]

这就是最大切应力理论的强度条件。可见莫尔强度理论实际上是第三强度理论的推广。它不但可用于塑性材料，也可以用于铸铁等脆性材料，特别适用于抗拉和抗压强度不同的材料。它广泛地应用于土力学、岩石力学、地质力学。其不足之处是，与最大切应力理论一样，没有考虑中间主应力σ2。不过σ2对材料的影响较小，在极端情况下不超过15%，大多数情况下由于未考虑σ2，所引起的误差更小。

【例5.7】 一铸铁零件，在危险点处的应力状态主应力σ1＝24MPa，σ2＝0，σ3＝－36MPa。已知材料的[σl]＝35MPa，ν＝0.25，试校核其强度。

解：因为铸铁是脆性材料，因此选用第二强度理论，其相当应力

σxd2＝σ1－ν（σ2＋σ3）＝24－0.25×（0－36）＝33（MPa）＜[σl]＝35MPa

所以零件是安全的。

如果采用第三强度理论，其相当应力

σxd3＝σ1－σ3＝24－（－36）＝60（MPa）＞[σl]＝35MPa

即按第三强度理论计算，零件不安全，但实际是安全的，这是因为铸铁属脆性材料，不适合于应用第三强度理论。

【例5.8】 图5.25（a）所示的简支梁，F＝100k N，梁的截面是20a工字钢，材料为2号钢，许用应力[σ]＝150MPa，[τ]＝90MPa，试对梁进行强度校核。

图5.25(www.xing528.com)

解：（1）确定危险截面。画出梁的剪力图和弯矩图如图5.25（b）、（c）所示。由图可知，C、D截面为危险截面，因其数值相等，故选择其中一截面，选C截面进行强度校核。

（2）校核最大正应力及最大切应力。由型钢表查得20a工字钢有关数据，Iz＝2370cm4，W＝237cm3，Iz/S＝17.2cm，d＝7mm。

由正应力强度条件

即正应力满足强度要求。

切应力也满足强度要求。

（3）应用强度理论校核。危险截面上的剪力、弯矩具有最大值，在截面的腹板与翼缘交接处的正应力和切应力同时有较大的数值，因此该处的主应力可能很大，是危险点，选择该处进行强度校核，为此在该处取K1、K2点[图5.25（d）]，围绕该点取单元体，计算单元体上的应力

将以上应力标到单元体上，如图5.25（e）所示。计算主应力：

由主应力排序的有关规定，则σ1＝28.36MPa，σ2＝0，σ3＝－148MPa。

因工字钢材料是2号钢，属塑性材料，故采用第四强度理论校核：

故不满足强度要求（计算得的σxd4已超过了[σ]的5%），需另选较大的截面。

（4）重新选择截面。改选为20b工字钢，查得I＝2500cm4，腹板厚度d＝9mm，翼缘宽度b＝102mm，其余尺寸与20a相同。重复以上计算得

即满足强度要求，故选用20b工字钢。

【例5.9】 水库岸边为花岗岩体。已知花岗岩的许用拉应力为2MPa，许用压应力为16MPa，库岸岩体内危险点的主应力σ1＝－4MPa，σ3＝－26MPa。试用莫尔强度理论对岸边岩体进行强度校核。

解：由莫尔强度条件得

可知水库岸边岩体强度足够。