超静定梁设计简介

前面所讨论的梁，其约束反力都可以通过静力学平衡方程求得，这样的梁称为静定梁。在工程实际中，有时为了提高梁的强度和刚度，或者因构造上的需要，除了维持其平衡所必需的约束之外，还需增加约束。这时，未知反力的数目将多于平衡方程的数目，仅由静力平衡方程不能求解，这样的梁称为超静定梁。

在超静定梁中，凡是多于维持平衡所必需的约束，称为多余约束，相应的支反力或支反力偶统称为多余支反力。多余支反力的数目称为超静定次数（或超静定度）。如图4.21（a）、（b）所示梁便分别是一次和两次超静定。

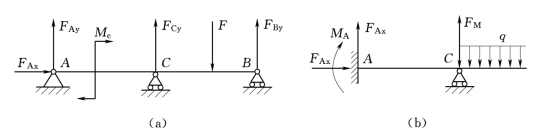
图4.21

解超静定梁的方法很多，变形比较法是最基本的一种。为了求解超静定梁，除建立平衡方程外，还应利用变形协调条件及力与位移间的物理关系建立变形补充方程。现以图4.22（a）所示梁为例，说明变形比较法的基本步骤。

该梁具有一个多余约束，即具有—个多余支反力。如果选择支座B为多余约束，相应的多余支反力为FBy。为了求解，假想地将支座B解除，代之以支反力FBy，于是得一承受荷载F与未知支反力FBy的静定悬臂梁如图4.22（b）所示。此静定梁的受力与原超静定梁完全相同，称为原超静定梁的相当系统。相当系统在原荷载与多余约束力FBy共同作用下产生变形，按等效替代原则，相当系统的变形应与原超静定梁完全相同，多余约束处的位移必须符合原超静定梁在该处的约束条件，即满足变形协调条件。

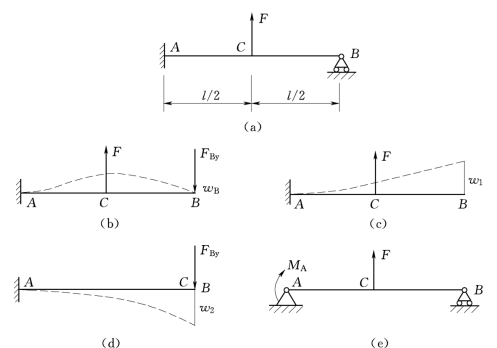
图4.22

在本例中，原超静定梁在支座B处的位移约束条件为

wB＝0

所以相当系统在F与FBy共同作用下，B处的挠度也应等于零，如图4.22（b）所示，即

wB＝w1＋w2＝0（补充方程）

利用积分法或叠加法[图4.22（c）、（d）]，易得

w1＝5l3 F/48EI（↑）

w2＝－l3 FBy/3EI（↓）

将w1、w2代入得变形补充方程

（5l3 F/48EI）－（l3 FBy/3EI）＝0

由此解得

FBy＝5F/16（↓）

所得结果为正，表明所设支反力FBy与实际方向一致。

多余支反力确定后，由平衡条件易得固定端处的支反力与支反力偶分别为

FAy＝11F/16（↓）

MA＝3Fl/16（逆时针）

应该指出，只要不是限制梁刚性位移所必需的约束，均可选为多余约束。如对图4.22（a）所示超静定梁，也可将固定端A选为多余约束。如果将该约束解除，用反力偶MA代之，则原超静定梁的相当系统如图4.22（e）所示，相应的变形协调条件变为

θA＝0

由此求得的支反力与支反力偶与上述解答完全相同。(www.xing528.com)

以上分析表明，求解超静定梁的关键是确定多余支反力。现将分析方法和步骤归纳如下：

（1）根据支反力与独立平衡方程的数目，判断梁的超静定次数。

（2）选择相同数目的多余约束（限制梁刚性位移所必需的约束不在可选之列）。

（3）解除多余约束，并以相应多余支反力代替，得原超静定梁的相当系统。

（4）计算相当系统在多余约束处的位移，并根据相应的变形协调条件建立变形补充方程，与平衡方程联立解出所有约束反力。

约束反力确定后，作用在相当系统上的所有外力均为已知，即可通过相当系统计算原超静定梁的内力、应力和位移等。

【例4.10】 一悬臂梁AB，承受集中荷载F作用，因其刚度不够，用一短梁加固，如图4.23（a）所示。试计算梁AB的最大挠度的减少量。设二梁各截面的弯曲刚度均为EI。

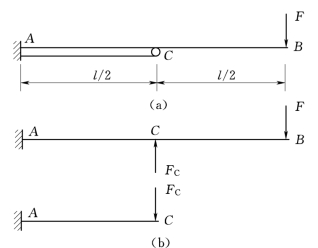
图4.23

解：梁AB与梁AC均为静定梁，但由于截面C处用铰相连，增加了一个约束，所以此结构为一次超静定结构，需要建立一个补充方程才能求解。

如果选择铰C作为多余约束予以解除，代之以FC，则原结构的相当系统如图4.23（b）所示。

梁AC在多余力FC作用下，其截面C铅垂下移w1；梁AB在荷载F与多余力FC共同作用下，其截面C也铅垂下移w2。变形协调条件为

查表4.1得

查表4.1得并利用叠加法得

将式（b）和式（c）代入式（a）得变形补充方程为

FC l3/24EI＝（5F－2FC）l3/48EI

解得

FC＝5F/4

加固前，梁AB的端点挠度即为最大挠度

Δ＝Fl3/3EI（↓）

加固后，该截面的挠度变为

Δ＇＝（Fl3/3EI）－（5FC l3/48EI）＝13Fl3/64EI（↓）

仅为前者的60.9%，由此可见，加固后的梁，其最大挠度明显减小。