简单拉压超静定技术

为了确定超静定问题的未知力，除应利用平衡方程外，还必须研究变形，并借助变形与内力间的关系，建立足够数量的补充方程。现以图4.19（a）所示超静定结构为例，介绍分析方法。

设杆1和杆2的抗拉压刚度分别为E1 A1和E2 A2、杆长l1＝l2＝a，现在分析在竖向荷载F作用时各杆的轴力和支反力。

在荷载F作用下，设两杆均受拉，选取杆AB为研究对象，受力如图4.19（b）所示。其平衡方程为

∑Fy＝0

∑MA＝0

显然，利用上述平衡方程还不能求解未知力。

由于AB杆为刚性杆，在F作用下，绕A发生刚体转动，两杆则均发生伸长变形、故结构的变形如图4.19（b）所示。为保证结构的完整性和连续性，杆1的变形Δl1和杆2的变形Δl2之间应满足如下几何关系：

保证结构完整性和连续性所应满足的变形几何关系，称为变形协调条件或变形协调方程。变形协调方程是求解超静定问题的补充条件，再利用物理关系，将变形协调方程用轴力表示，得出求解超静定问题的补充方程。

由胡克定律可知。两杆的变形与相应的轴力间有以下关系

Δl1＝FN1l1/E1A1＝FN1a/E1A1

Δl2＝FN2l2/E2 A2＝FN2a/E2 A2

将上述关系式代入式（c），得到用轴力表示的变形协调方程，即

联立平衡方程式（4.29）与式（4.30）和补充方程（d）得

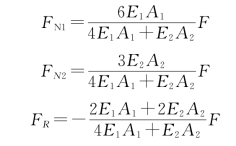
FN1和FN2结果均为正，表明所设杆轴力方向与实际相同。FR为负，说明与实际相反。

由以上解答可以看出，对超静定结构，杆的轴力和支反力与各杆的抗拉压刚度的比值有关。一般而言，增大某杆刚度，该杆的轴力也相应增大；改变任一杆的刚度，都将引起结构中所有杆件轴力的重新分配，这是超静定结构区别于静定结构的一个重要特点。

综上所述，求解超静定问题应从静力学平衡、变形协调及力与变形间的物理关系三个方面进行综合分析，然后建立静力平衡方程、变形协调方程联立求解。

【例4.9】 图4.20（a）所示等截面杆AB，两端固定，在横截面C处承受轴向载荷F作用。试求杆的轴力。(www.xing528.com)

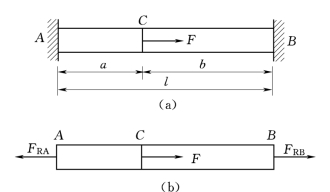
图4.20

解：（1）静力学分析。解除杆端约束，代之于支反力FRA和FRB。其受力如图4.20（b）所示。由于是共线力系，故仅可列一个独立平衡方程，即

而式中有两个未知力，故为一次超静定问题。

（2）几何分析。根据杆两端的约束条件可知，受力后各杆段虽变形，但杆的总长不变，AB杆的总伸长ΔlAB为零，如果将AB与CB段的轴向变形分别用ΔlAC与ΔlBC表示，则变形协调条件为

（3）物理分析。用截面法，AC与CB段的轴力分别为

FN1＝FRA

FN2＝FRB

所以轴向变形为

（4）支反力计算。将式（c）和式（d）代入式（b）得补充方程为

联立平衡方程式（a）和补充方程式（e），得

FRA＝a F/l

FRB＝－bF/l

负号表示FRB所设方向与实际方向相反。

最后，得AC与BC段的轴力分别为

FN1＝b F/l（拉）

FN2＝－a F/l（压）