梁的刚度计算方法详解

1.梁的刚度条件

工程上，对于弯曲构件，除了要满足强度条件外，还经常要满足刚度要求，对弯曲变形加以限制，所以在用强度条件设计梁的截面尺寸后，还必须进行刚度校核，刚度条件为

式中：[w]为许用挠度；[θ]为许用转角。其值由具体工作条件确定，对不同变形要求的构件有不同的规定，可从相应的设计规范或手册中查得。例如，对跨度为l的桥式起重机梁，其许用挠度为

[w]＝l/750～l/500

又如，对一般用途的轴，其许用挠度为

[w]＝（3l/10000）～（5l/10000）

再如，在安装齿轮或滑动轴承处，轴的许用转角为

[w]＝0.001rad

在设计计算时，一般是根据强度条件先确定构件的截面尺寸，然后再进行刚度校核。

【例4.8】 图4.14（a）所示为一台起重量为50k N的单梁桥式吊车简图。已知电葫芦重5k N，吊车梁跨度l＝9.2m，采用45a号工字钢，许用挠度[w]＝l/500试校核该吊车梁的刚度。

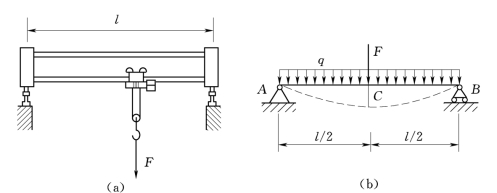
图4.14

解：将吊车梁简化为如图4.14（b）所示的简支梁。电葫芦的轮压近似地视为一集中力F，并作用于梁的中点（此时由F引起的挠度最大）；梁的自重为均布荷载，集度为q

（1）计算有关数据。

F＝50＋5＝55（k N）

查型钢表得

q＝80.42kgf/m＝788k N/m

I＝3.22×10－4 m4

材料弹性模量

E＝200GPa

（2）计算最大挠度。因F和q产生的最大挠度均位于梁的中点C，查表4.1得

wC，F＝Fl3/48EI＝1.39（cm）（↓）

wC，q＝5ql4/384EI＝0.114（cm）（↓）(www.xing528.com)

由叠加法，得梁的最大挠度

wmax＝1.39＋0.114＝1.5（cm）

（3）校核刚度。吊车梁的许可挠度为

[w]＝l/500＝9.2/500＝1.84（cm）

比较梁的最大挠度，知

wmax＝1.5cm＜[w]＝1.84cm

故该吊车梁满足刚度要求。

2.梁的合理刚度设计

综合前述对梁变形的讨论结果，其挠度和转角可统一表示为如下形式：

从式（4.26）可以看出，影响梁变形（挠度、转角）的主要因素有：梁的长度l、弯曲刚度EI和梁上作用载荷的类别及其分布状况。要提高梁的刚度，减小梁的变形，应从上述三个方面采取措施。

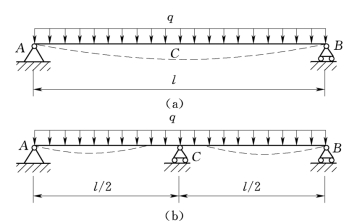
图4.15

（1）缩短梁的长度，增加支撑约束。式（4.26）中l的上角标n的值与载荷的类型有关，若在式中视为位移挠度，在载荷分别为集中力偶、集中力、均布载荷时，n值分别为2、3、4，可见，梁的跨度对梁变形的影响较大，因此，如果条件允许，尽量减小梁的跨度可使梁的变形减小。

当梁的挠度较大时，可通过增加支撑或约束减小挠度。例如，在图4.15（a）所示简支梁的跨中增设一个铰支座C图4.15（b），其最大挠度仅为增设前的2.5%。增加支撑或约束，减小了梁的变形，但也使梁变为超静定结构。

（2）增大梁的弯曲刚度，选用合理截面。梁的弯曲刚度EI与梁的变形成反比，因此，提高梁的抗弯刚度同样也可以减小梁的变形。由于各种钢材（包括各种普通碳素钢、优质合金钢）的弹性模量数值相差很小，故通过选择优质钢材来提高梁的弯曲刚度决非明智之举。设法增大截面的惯性矩I才是提高梁弯曲刚度的有效途径。即选用合理截面，以较小的截面面积取得较大的惯性矩。例如，自行车架由圆管焊接而成，不仅增加了车架的强度，也提高了车架的弯曲刚度。

对一些原来刚度不足的构件，也可以通过增大惯性矩的措施减小其变形，如在工字梁上、下翼缘处加焊钢板等。

（3）调整加载方案，改善结构设计。通过调整加载方式，降低梁的弯矩值，也可减小梁的变形。例如，图4.16（a）所示跨中受集中力作用的简支梁，将集中力改变为作用在全梁上的均布载荷，如图4.16（b）所示，其最大挠度仅为调整前的62.5%。

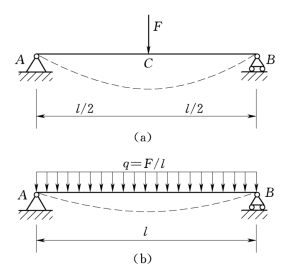
图4.16

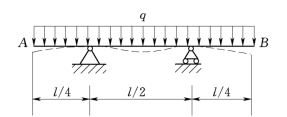
图4.17

改善结构设计，合理安排支撑或约束，可大幅度降低弯矩值，从而使梁的变形得到显著减小。图4.17所示跨度为l的简支梁，受均布荷载q作用，如果将梁两端的铰支座各向内移动l/4，如图4.17所示，则其最大挠度将仅为前者的8.75%。

从上述讨论可见，对梁进行合理刚度设计与前章所述对梁进行合理强度设计有异曲同工之处，但需要指出的是，梁的合理刚度设计与梁的合理强度设计，是属于两种不同性质的问题，因此其解决问题的出发点及其方法也不尽相同。