使用叠加法求梁的变形

积分法是求梁变形的一种基本方法，但在工程实际中，梁上一般都同时作用若干个荷载，此时若用上述积分法来计算，其计算过程过于繁琐。在此情况下，用叠加法计算梁的变形就相对简便。

为了应用叠加法和实用的方便，将各种简单荷载作用下梁的挠曲线的方程式及挠度与转角公式列于表4.1，以备查用。

表4.1　梁的挠曲线方程及挠度与转角

续表

在小变形条件下，且当梁内应力不超过比例极限时，挠曲线近似微分方程是线性的，梁内任一横截面的弯矩与荷载成线性关系。

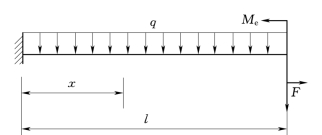
图4.11

既然挠曲线近似微分方程是线性微分方程，而弯矩又与荷载呈线性关系。因此当梁上同时作用几个荷载时，挠曲轴近似微分方程的解，等于各荷载单独作用时挠曲线近似微分方程解的线性组合，由此求得的挠度与转角也与荷载呈线性关系。

当梁上同时作用几个荷载时，可分别求出每一荷载单独作用所产生的变形，叠加后即为所有荷载共同作用时产生的变形。这就是计算梁变形的叠加法。如对图4.11所示梁，若设荷载q、F与Me单独作用时截面A的挠度分别为wq，wF与wM，则它们共同作用时该截面的挠度为

【例4.6】 简支梁所受荷载如图4.12（a）所示，试用叠加法求梁跨中点的挠度和支座处的转角θA和θB。

解：（1）求挠度。当梁上只受中点集中力F作用时，如图4.12（b）所示，查表得C点的挠度为

wC，F＝Fl3/48EI（↑）

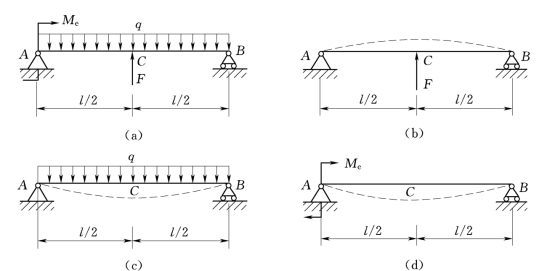
图4.12

当梁上只受均布荷载q作用时，如图4.12（c）所示，查表得C点的挠度为

wC，q＝－5ql4/384EI（↓）

当梁在左端点处只受集中力偶作用时，如图4.12（d）所示，查表得C点的挠度为

wC，M＝－Ml2/16EI（↓）

故C点的总挠度为

wC＝wC，F＋wC，q＋wC，M＝（Fl3/48EI）－（5ql4/384EI）－（Ml2/16EI）

（2）求转角。当梁上只受中点集中力F作用时，如图4.12（b）所示，查表得A、B面的转角为

θA，F＝－θB，F＝Fl3/16EI（逆时针）(www.xing528.com)

当梁上只受均布荷载q作用时，如图4.12（c）所示，查表得A、B面的转角为

θA，q＝－θB，q＝－ql3/24EI（顺时针）

当梁在左端点处只受集中力偶作用时，如图4.12（d）所示，查表得A、B面的转角为

θA，M＝－Ml/3EI（顺时针）

θB，M＝＋Ml/6EI（逆时针）

故A、B面的总转角分别为

θA＝θA，F＋θA，q＋θA，M＝（Fl3/16EI）－（ql3/24EI）－（Ml/3EI）

θB＝θB，F＋θB，q＋θB，M＝－（Fl3/16EI）＋（ql3/24EI）＋（Ml/6EI）

需要注意的是，查表4.1时，要根据外力的实际方向确定变形的正负，不要盲目照抄书上的公式。

利用叠加法，对表4.1中没有列出的某些类型的梁（如外伸梁、阶梯梁等）如果对其稍加分析和处理，也可利用表中公式按叠加法计算变形，即所谓逐段分析求和法。下面举例予以阐明。

【例4.7】 外伸梁承受荷载如图4.13（a）所示，试用叠加法计算外伸端C截面的挠度。

解：为了计算C截面的挠度，可将该梁看作是由简支梁AB与固定在横截面B的悬臂梁BC所组成，当简支梁AB与悬臂梁BC变形时，均在截面C引起挠度，而其总和即为该截面的总挠度。

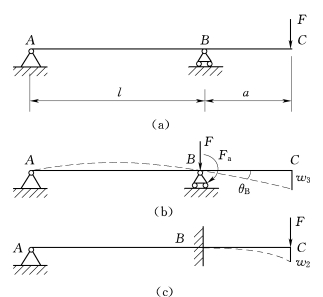
图4.13

为了分析简支梁AB的变形，将荷载F平移到截面B，得作用在该截面的集中力F与矩为Fa的附加力偶如图4.13（b）所示，于是截面B的转角为

θB＝－Fal3/3EI

由于此时可将BC视为刚性转动。故得截面C的相应挠度为

w1＝aθB＝－Fla2/3EI（↓）

在荷载F作用下，如图4.13（c）所示，悬臂梁BC的端点挠度为

w2＝－Fa3/3EI（↓）

于是截面C的总挠度为

wC＝w1＋w2＝－（Fa2/3EI）（a＋l）（↓）

上述分析方法的要点是：首先分别计算各梁段的变形在待求位移处引起的位移，然后计算其总和（代数和或矢量和）。在分析各梁段的变形在待求位移处引起的位移时。除所研究的梁段发生变形外，其余各梁段均视为刚体。例如，在计算图4.13（b）所示挠度时，只将梁段AB视为变形体，而将梁段BC视为刚体。

叠加法与逐段分析求和法的共同点是综合应用已有的计算结果。不同点是，前者是分解荷载，后者是分解梁，前者的理论基础是力作用效果的独立性，后者的根据是梁段局部变形与总体位移间的几何关系。由于在实际求解时，一般是将两种方法联合应用，所以又将二者统称为叠加法。