梁的挠曲线近似微分方程与积分法

1.梁的挠曲线近似微分方程

在纯弯曲时，由第3章公式（3.53），即

当梁的跨度远大于横截面高度时，剪力对梁变形的影响甚微，故上式也可用于一般横力弯曲。在这种情况下，由于弯矩M与曲率半径ρ均为x的函数，上式可变为

由高等数学可知，平面曲线上任一点的曲率为

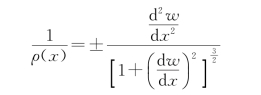
将其代入式（4.17）得

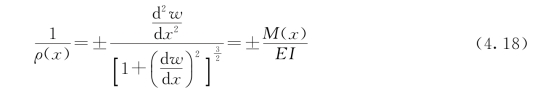
式（4.18）称为挠曲线微分方程，它是一个二阶非线性常微分方程。显然，求解这样的方程是相当困难的，但在工程实际中，梁的转角一般均很小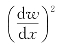，之值远远小于1，所以，式（4.18）可简化为

式（4.19）称为挠曲线近似微分方程，它已简化为一个二阶线性常微分方程，实践证明，由方程求得的挠度与转角，对于工程应用已足够精确。

至于方程式（4.19）的符号，应由坐标系的选取和弯矩的符号确定。由于坐标系已经选定，如图4.6所示，弯矩的符号如前所规定，因此，方程式4.19的符号即可唯一确定。如图4.7所示，当梁段承受正弯矩时，挠曲线下凹。如图4.7（a）所示，d2 M/d x2应为正；反之，当梁段承受负弯矩时，挠曲轴上凸。如图4.7（b）所示，d2 M/d x2应为负。可见，如果选用w轴向上的坐标系，则弯矩M与d2w恒为同号，方程式（4.19）的右端应取正号，故挠曲轴近似微分方程为

即

EIw″＝M（x）

应该指出，由于x轴的方向既不影响弯矩的正负，也不影响d2 w/d x2的正负，所以，式（4.20）同样适用于x轴向左的坐标系。

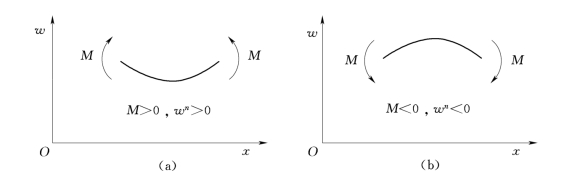
图4.7

2.位移边界条件与连续条件

将挠曲线近似微分方程积分两次，得

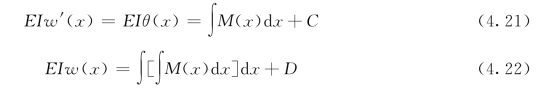
式中：C与D为积分常数，由梁的已知位移边界条件和连续性条件确定。

所谓已知位移边界条件，指梁上某些截面的已知位移。例如，在固定端处截面的挠度与转角均为零，即

w＝0，θ＝0

在铰支座处横截面的挠度为零，即

w＝0

所谓连续性条件，指分段交界处挠曲线相应满足的连续、光滑条件。当梁上的外力将梁分为数段时，各段梁的弯矩方程不同，因而梁的挠曲线近似微分方程也需分段列出，各相应段梁的转角方程和挠曲线方程也随之而异，但相邻梁段的交界处为同一截面，其挠度与转角应完全相同，这就是梁位移的连续性条件。

积分常数确定后，将其代入式（4.21）与式（4.22），即得到梁的挠曲线方程

w＝w（x）

和转角方程

θ＝θ（x）＝d w（x）/d x＝w＇（x）

由此可求出任一横截面的挠度与转角。

由以上分析可以看出，梁的位移不仅与梁的弯曲刚度及弯矩有关，而且与梁位移的已知位移边界条件及连续性条件有关。

3.计算梁变形的积分法

按式（4.21）和式（4.22）进行积分，再根据已知位移边界条件和连续性条件确定积分常数，便可得到梁的挠曲线方程，利用挠曲线方程可求任一横截面的挠度和转角。这种方法称为积分法。

【例4.4】 悬臂梁AB，在自由端B作用一集中力F，如图4.8所示。试求梁的转角方程和挠曲线方程，并确定最大转角|θ|max和最大挠度|w|max。

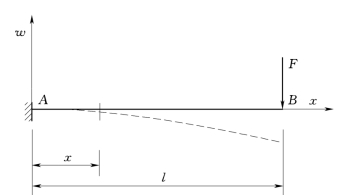
图4.8

解：以梁左端A为原点，取一直角坐标系，令x轴向右，w轴向上。

（1）弯矩方程。在距端点x处取截面，列出弯矩方程为

（2）列挠曲线近似微分方程并进行积分。将弯矩方程代入式（4.20），得

通过两次积分得

（3）确定积分常数。悬臂梁在固定端处的挠度和转角均为零，即在x＝0处

θA＝w＇A＝0，wA＝0

将两个边界条件代入式（c）和式（d），得

C＝0，D＝0

（4）确定转角方程和挠曲线方程。将求得的积分常数C和D代入式（c）和式（d）得梁的转角方程和挠曲线方程为

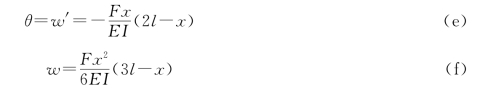
（5）求最大转角和最大挠度。由图4.8可以看出，自由端B处的转角和挠度最大，以x＝l代入式（e）和式（f）得

θB＝－Fl2/2EI

|θ|max＝Fl2/2EI

wB＝－Fl3/3EI

即

|w|max＝Fl3/3EI

所得结果中，转角为负值，说明横截面绕其中性轴顺时针方向转动；挠度为负值说明B点的位移向下。(www.xing528.com)

【例4.5】 简支梁如图4.9所示，在全梁上受集度为q的均布载荷作用。试求此梁的转角方程和挠曲线方程，并确定最大转角|θ|max和最大挠度|w|max。

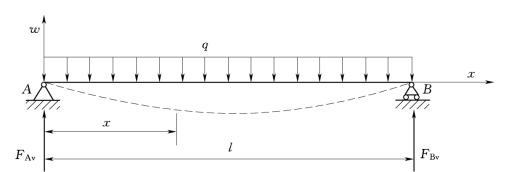
图4.9

解：以梁左端A为原点，取一直角坐标系，令x轴向右，w轴向上。

（1）列出梁的弯矩方程为

（2）列挠曲线近似微分方程并进行积分，由式（4.20）得

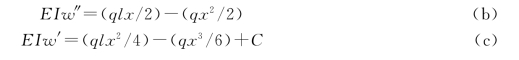
通过两次积分得

（3）确定积分常数，简支梁的已知位移边界条件是：在两支座处的挠度等于零，即：在x＝0处

wA＝0

将其代入式（d）得

D＝0

在x＝l处

wB＝0

将其代入式（d）得

wB＝（ql4/12）－（ql4/24）＋Cl＝0

由此解得

C＝－ql3/24

（4）确定转角方程和挠曲线方程，将求得的积分常数C和D代入式（c）和式（d）得梁的转角方程和挠曲线方程为

（5）求最大转角和最大挠度，梁上载荷和边界条件均对称于梁跨中点C，故梁的挠曲线也必对称。由此可知，最大挠度在梁的中点处，以x＝l/2代入式（f）得

wC＝－5ql4/384EI

|w|max＝5ql4/384EI

式中：负号表示梁中点的挠度向下。

又由图4.9可见，在两支座处横截面的转角相等，均为最大。由式（e）得

在x＝0处

θA＝－ql3/24EI

在x＝l处

θB＝＋ql3/24EI

故

|θ|max＝ql3/24EI

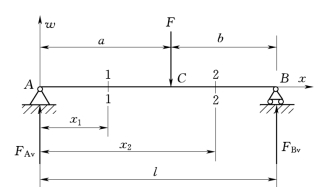
图4.10

式中：负号表示截面为顺时针方向转动；正号表示截面为反时针方向转动。

[例4.4]和[例4.5]都只需对全梁列出一个挠曲线近似微分方程，但当梁的挠曲线近似微分方程分段列出时，积分后每段均将出现两个积分常数。为确定这些积分常数，除利用已知位移边界条件外，还需利用分段处的连续性条件。例如，图4.10所示的简支梁，集中力F将全梁分为AC、CB两段，这时两段梁的挠曲轴近似微分方程及其积分分别为

AC段（0≤x1≤a）

EIw1″＝Fbx1/l

EIw1＇＝Fb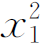/2l＋C1

EIw1＝Fb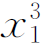/6l＋C1 x1＋D1

CB段（a≤x2≤l）

EIw2″＝Fbx2/l－F（x2－a）

EIw2＇＝Fb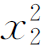/2l－F（x2－a）2/2＋C2

EIw2＝Fb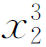/6l－F（x2－a）3/6＋C2 x2＋D2

积分后一共求出4个积分常数，需要4个已知的边界条件才能确定。

简支梁的已知位移边界条件有两个，即

在x1＝0处

w1＝wA＝0

在x2＝l处

w2＝wB＝0

简支梁在分段处的连续性条件也有两个，即

在x1＝x2＝a处

w1＇＝w2＇（即θ1＝θ2）

w1＝w2

用这两个连续性条件和两个已知位移边界条件即可确定4个积分常数。积分常数确定后，两段梁的转角方程和挠曲线方程也就可以求得。以下的演算与前面两例类似，读者可自行演算，其结果为

w1＝（Fbx1/6l EI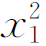）（－l2＋b2）（0≤x1≤a）

w2＝[Fa（l－x2）/6l EI]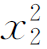（－a2＋2lx2）（a≤x2≤l）