泊松比和胡克定律简介

1.泊松比

试验表明，在一定应力范围内，横向线应变ε＇与轴向线应变ε之间保持比例关系，但符号相反，即

式中：比例系数μ称为泊松比或横向变形系数，μ是一无量纲的量，其值随材料而异，由试验测定。

2.拉压胡克定律

下面讨论轴向拉压杆的变形规律和计算。当拉压杆受轴向力作用后，杆中横截面上产生正应力σ，相应的产生轴向正应变ε。试验表明，在一定的应力数值范围以内，一点处的正应力σ与该点处的正应变ε成正比关系，即

式（4.6）称胡克定律，比例系数E称为材料的弹性模量，其值随材料而异，需通过试验测定。由式（4.6）可以看出，由于正应变ε是—个无量纲的量，所以，弹性模量的量纲与正应力σ的量纲相同，即为MPa或Pa。

需要指出的是，弹性模量E和泊松比μ都是表征材料弹性性质的常数，与材料性质有关，与杆件所受荷载等外因无关。

3.拉压杆的变形公式

现在利用胡克定律导出拉压杆的轴向变形Δl的计算公式。

设杆件横截面面积为A，轴向拉力为F，如图4.1所示，则横截面上的正应力

将式（4.2）代入式（4.6）和式（4.7）得

FN/A＝E（Δl/l）

所以　

式（4.8）即为计算拉压杆变形的公式，这个公式是胡克定律的另一种表达形式，它表明：在正应力与正应变存在正比关系的范围以内，杆的伸长量Δl与轴力和杆长l成正比，而与乘积EA成反比。

对于式（4.8）应注意以下几点：

（1）轴向变形Δl与杆的原长l有关，因此，轴向变形Δl不能确切地表明杆件的变形程度。只有正应变ε才能衡量和比较杆件的变形程度。(www.xing528.com)

（2）式中EA与杆的轴向变形Δl成反比，可见，乘积EA反映杆件抵抗拉压变形的能力，故称EA为杆件的拉压刚度。

（3）轴向变形Δl的正、负（伸长或缩短）与轴力的符号相同。

（4）此式只适用于E、A和杆段内轴力FN均为常数的变形计算。

如果全杆的轴力FN、截面面积A和弹性模E其中之一是分段变化时，则应按式（4.8）分段计算每杆段的轴向变形，然后求其代数和，即得全杆总的轴向变形Δl，即

如果FN或A沿轴线连续变化，则全杆总的轴向变形应通过微段d x的轴向变形d（Δl），积分计算，即

【例4.1】 如图4.2（a）所示，为一阶梯形钢杆，已知材料的弹性模量E＝200GPa，AC段的横截面面积为AAB＝ABC＝500mm2，CD段的横截面面积为ACD＝200 mm2，杆的各段长度及受力情况如图所示。试求杆的总变形。

解：（1）求各段的内力。

AB段　FN1＝F1－F2＝30k N－10k N＝20k N

BC段与CD段　FN2＝－F2＝－10k N

（2）画轴力图，见4.2（b）。

图4.2

（3）杆的总变形等于各段杆变形的代数和，即

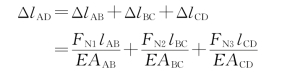
将有关数据代入，并注意单位的统一，即得

ΔlAB＝－0.015×10－3 m＝－0.015mm

负值说明整个杆件是缩短的。