提高梁强度的有效方法

梁是工程中最常见的一种构件。在设计梁时，既要节省材料、减轻梁的自重，又要尽量提高梁的强度，来满足工程上既安全又经济的要求。如前所述，由于弯曲正应力是控制梁强度的主要因素，因此，提高梁强度的措施，必须以弯曲正应力强度条件作为主要依据，即

从上式可以看出，要提高梁的承载能力，一方面要合理安排梁的受力情况，以降低Mmax的数值，另一方面应采取合理的截面形状，充分利用材料，以提高Wz的数值。下面将常用的几种措施分述如下。

1.合理配置梁的荷载和支座

合理地配置梁上荷载，可降低梁的最大弯矩值。如图3.62（a）所示简支梁跨中承受集中力F作用，梁的最大弯矩为。若采用一个辅梁，使集中力通过辅梁再作用到梁上[图3.62（b）]，则梁的最大弯矩降低为。

图3.62

同理，合理安排支座位置，也可降低梁内的最大弯矩。如图3.63（a）所示简支梁承受均布荷载q作用，其跨中最大弯矩。若将两端支座各向里移动0.2l[图3.63（b）]，则最大弯矩减小为，仅为前者的。

2.合理选取梁的截面

当弯矩一定时，截面上的最大正应力与弯曲截面系数成反比，因此，增大弯曲截面系数W和减小截面面积，就能达到提高梁的强度和减轻自重的目的。所以，合理的截面形状，应该是截面的弯曲截面系数W与其面积A之比尽可能地大。例如对于截面高度h大于宽度b的矩形截面梁，如把它竖放[图3.64（a）]，则；若把它平放[图3.64（b）]，则。两者之比是

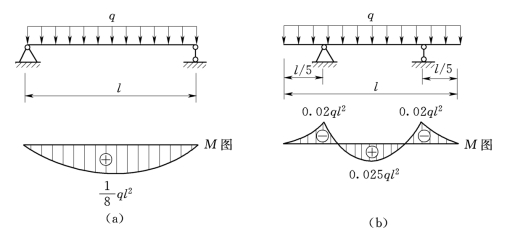
图3.63

图3.64

可见竖放比平放有较高的抗弯强度。在土建工程中，矩形截面梁一般都应竖放的。

在表3.3中，列出了几种常用截面的Wz和A的比值。从表中所列数值看出，工字形截面或槽形截面比矩形截面经济合理，矩形截面比圆形截面经济合理。究其原因，是由于抗弯截面模量Wz与截面高度的平方成正比。若将较多的材料分布到距中性轴较远处，就能充分发挥材料的潜力，提高梁的承载能力。因此，在工程中常将实心圆截面改为空心圆截面，将矩形截面改为工字形、箱形等。

表3.3　几种截面的Wz与A的比值

在选取合理截面形状时，还应考虑材料的特性。对抗拉和抗压强度相等的塑性材料（如低碳钢），宜采用以中性轴为其对称轴的截面，如圆形、矩形、工字形等，这样可使截面上、下边缘处的最大拉（压）应力相等，且同时接近许用应力。对抗拉和抗压强度不等的脆性材料（如铸铁），宜采用T形等（图3.65）对中性轴不对称的截面，并将翼缘部分置于受拉侧。对于这类截面，应使y1和y2之比接近下列关系：

(www.xing528.com)

式中：[σt]和[σc]分别为许用拉应力和许用压应力。

上式表明，梁内最大弯矩截面上的最大拉（压）应力同时接近许用应力。这样，就能充分利用材料的特性。

3.合理设计梁的外形

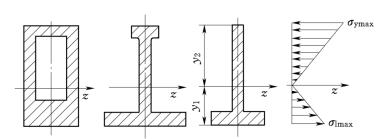
图3.65

前面讨论的是等截面直梁，W＝常数，但梁在各截面上的弯矩却随截面的位置而变化。只有在弯矩为最大值的截面上，最大应力才有可能接近许用应力。其余各截面上弯矩较小，应力也就较低，材料没有充分利用。为了节约材料减轻自重可改变截面尺寸，使弯曲截面系数随弯矩而变化。即在弯矩较大处采用较大截面，而在弯矩较小处，采用较小截面。这种截面沿轴线变化的梁，称为变截面梁。例如，雨篷或阳台的悬臂梁常采用变截面梁，变截面梁的正应力计算仍可近似地用等截面梁的公式。

若使变截面梁各横截面上的最大正应力都相等，且均达到材料的许用应力，就是等强度梁。设梁在任一截面上的弯矩为M（x），而截面的弯曲截面系数为W（x）。根据上述等强度梁的要求，应有

或者写成

这是等强度梁的W（x）沿梁轴线变化的规律。

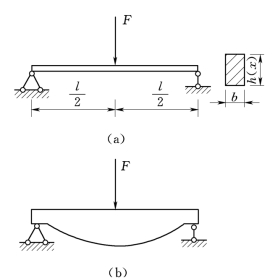
图3.66

例如，宽度不变而高度变化的矩截面简支梁（图3.66），若设计成等强度梁，则其高度随截面位置的变化规律h（x），由式（3.72）可求得

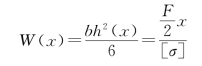
于是

但在靠近支座处，应按切应力强度条件确定截面的最小高度为

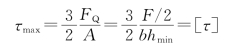
则　

以上主要是从弯曲强度的角度来考虑的，但在实际工程中，设计一个构件时，还应考虑刚度、稳定性、工艺条件、加工制造等多方面的因素。经综合考虑比较后，再正确地选用具体措施。