圆轴扭转的应力和强度条件

1.圆轴扭转时横截面上的应力

与薄壁圆筒相仿，在小变形条件下，实心圆轴扭转时横截面上也只有切应力。为了求得圆轴扭转时横截面上的切应力及分布规律，必须从几何、物理、静力学三个方面综合考虑来求解。

（1）几何方面。为了观察圆轴的扭转变形，与薄壁圆筒受扭一样，在圆轴表面画上一些圆周线和纵向线，如图3.30（a）所示。在圆轴的受扭后可观察到与薄壁圆筒受扭时相同的变形现象，即：圆周线的形状、大小及间距均没有改变，只是各圆周线绕轴线相对旋转了一个角度；纵向线都倾斜了相同角度γ，变形前的表面上矩形网格变成了平行四边形。

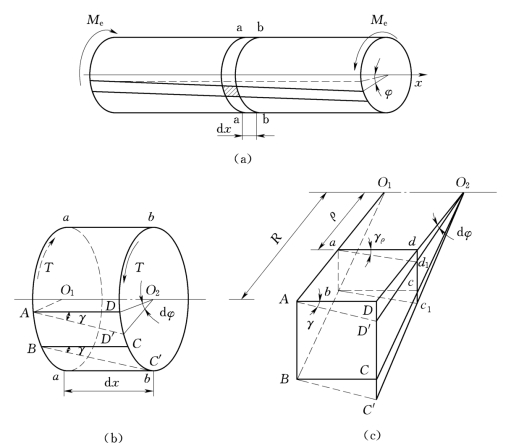
图3.30

根据上述变形现象，得出如下基本假设：圆轴扭转变形前原为平面的横截面，变形后仍保持平面，其形状和大小不变，且相邻两截面间的距离不变。这就是圆轴扭转的平面假设。按照这一假设，圆轴扭转时，其横截面就像刚性平面一样，绕轴线旋转了一个角度。

如图3.30（b）所示，从圆轴中截取长为d x的微段。根据上述变形现象，该微段表面上纵向线AD、BC均转了一个γ角，纵向线的倾角γ就是横截面周边上任一点D处的切应变；微段的b—b截面相对于a—a截面转过了一个角度dφ，因此其上的任意半径O2D也转动了同一角度dφ。再从微段中取出楔形块O1O2 ABCD，如图3.30（c）所示。由于扭转变形，使位于圆轴表面的矩形ABCD的CD边相对于AB发生微小的错动，错动的距离DD＇由几何关系可以求得

DD＇＝γd x＝R dφ

所以

这就是圆截面边缘上D点处的切应变。显然，γ发生在垂直于半径O2D的平面内。

根据变形后横截面仍为平面，半径仍为直线的假设，用相同的方法，可以求得距圆心为ρ处的剪应变，即

式中，表示扭转角φ沿轴线的变化率，对于给定的横截面来说，为一常数。故式（3.22）表明：横截面上任意点的剪应变γρ与该点到圆心的距离成正比，在同一圆周上，各点的剪应变γρ相同。

（2）物理方面。以τρ表示横截面上距圆心为ρ处的剪应力，由剪切胡克定律知

τρ＝Gγρ

将式（3.22）代入上式得

上式表明：横截面上任意点的剪应力τρ与该点到圆心的距离ρ成正比。由于γρ位于垂直于半径的平面内，所以τρ也与半径相垂直。由切应力互等定理，则在纵向截面和横截面上，沿半径切应力的分布如图3.31所示。

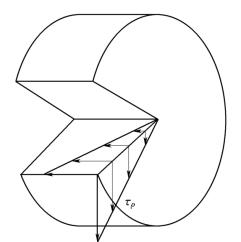
图3.31

（3）静力学方面。横截面上切应力变化规律表达式中的是个待定的参数，为了确定该参数，需考虑静力学方面的关系。如图3.32（a）所示，在圆轴的横截面上，距圆心为ρ的微面积d A处，作用有微内力τρd A，该微内力对圆心O之矩为ρτρd A。于是可得

将式（3.23）代入式（3.24），并注意到在给定的截面上，为常量，于是得

上式中的积分仅与横截面的几何量有关，称为横截面的极惯性矩，并用IP表示，即

将式（3.26）代入式（3.25），即得

式（3.19）表示了圆轴扭转时，单位长度扭转角与 扭矩T之间的关系。它是圆轴扭转变形的基本计算公式。

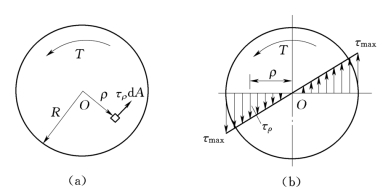
图3.32

将式（3.27）代入式（3.23），得

式（3.28）就是圆轴扭转时，横截面上任一点的剪应力计算公式。它表明，剪应力在横截面上是沿径向呈线性分布的，如图3.32（b）所示。最大剪应力τmax发生在横截面周边上各点处，其值为

引入记号

Wt称为抗扭截面系数，代入式（3.29），得

式（3.31）表明，圆轴扭转时，横截面上最大切应力与该截面上扭矩成正比，与抗扭截面系数成反比。

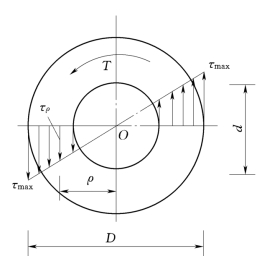
图3.33

以上切应力计算公式是以平面假设为基础导出的。试验结果表明，只有对等截面圆轴，平面假设是正确的。又由于导出以上诸式时使用了胡克定律。因此，这些公式适用于在线弹性范围内的等直圆杆。对于圆截面沿轴线变化缓慢的小锥度锥形杆，也可近似地采用以上公式计算。

由式（3.28）可知，实心圆轴扭转时，在靠近杆轴线处，切应力很小，使该处材料的强度不能得到充分利用。如果将圆轴中心部分材料移到周边处，就可充分发挥材料的作用。因而在工程中常采用空心圆截面杆。

由于圆轴扭转时的平面假设同样适用于空心圆轴，因此，前面得出的公式也适用于空心圆截面杆。空心圆轴扭转时的剪应力计算仍可采用式（3.28）和式（3.31）。只是式中的IP和Wt与截面的形状、尺寸有关，因此，与实心圆截面不相同。空心圆轴扭转时横截面上的切应力分布规律如图3.33所示。

导出式（3.27）和式（3.31）时，曾引进了截面极惯性矩IP和抗扭截面系数Wt，它们是与截面形状、尺寸有关的量。

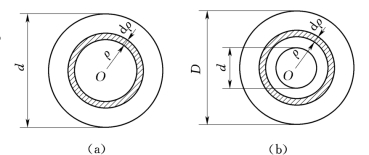
图3.34

对于实心圆截面，如图3.34（a）所示，在圆截面上距圆心为ρ处取厚度为dρ的环形面积作为微面积元素，即d A＝2πρdρ，并代入式（3.26），则极惯性矩为

将上式代入式（3.30），则得实心圆截面的抗扭截面系数为

对于空心圆截面，设其内外径分别为d和D[图3.34（b）]，其比值为 ，则由式（3.26）可得空心圆截面的极惯性矩为

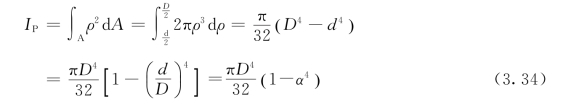
空心圆截面的抗扭截面系数为

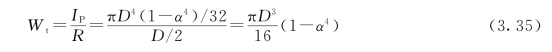
式中：IP的量纲是长度的四次方，常用单位为m4或mm4；Wt的量纲是长度的三次方，其常用单位为m3或mm3。

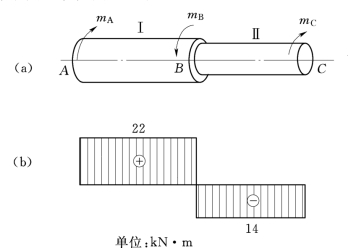
图3.35

【例3.6】 图3.35（a）所示阶梯状圆轴，AB段 直 径d1＝120mm，BC段 直 径d2＝100mm。外力偶矩mA＝22k N·m，mB＝36k N·m，mC＝14k N·m。试求该轴的最大剪应力τmax。

解：（1）求各截面的扭矩，并绘制扭矩图。用截面法求得AB、BC段的扭矩分别为

T1＝mA＝22k N·m，T2＝－mC＝－14k N·m

作出该轴扭矩图如图3.35（b）所示。

（2）计算最大切应力。由扭矩图可知，AB段的扭矩较BC段扭矩大。但因两段轴直径不同，因此需分别计算各段最大剪应力。由式（3.31）可得

AB段内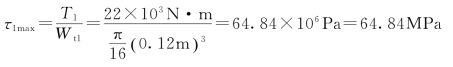：(www.xing528.com)

BC段内：

比较上述计算结果，该轴最大剪应力位于BC段内任一截面的周边各点处。

2.圆轴扭转时斜截面上的应力

前面我们讨论了圆轴扭转时横截面上的应力，已知横截面上周边各点处的切应力最大，为了全面了解杆内的应力情况，进一步讨论这些点处斜截面上的应力。为此，同前面一样在圆轴表面处截取一微小的单元体[图3.36（a）]，由前面的分析可知，该单元体处于纯剪切应力状态，即单元体前、后两侧面上无任何应力，左、右两侧面只有切应力τ，上、下两面也只存在切应力τ＇，且τ与τ＇满足切应力互等定理。由于单元体的前、后两面上无任何应力。故可将其改用平面图[图3.36（b）]表示。

图3.36

现分析在单元体内垂直于前后两平面的任一斜截面ef上的应力，设斜截面的外向法线n与x轴间的夹角为α，并规定从x轴至截面外向法线逆时针转动时α为正值，反之为负值。应用截面法，研究其左边部分[图3.36（c）]的平衡。设斜截面ef的面积为d A，则eb面和bf面的面积分别为d A cosα和d A sinα。选择参考轴ξ和η分别与斜截面ef平行和垂直[图3.36（c）]，由平衡方程

∑Fη＝0，σαd A＋（τd A cosα）sinα＋（τ＇d A sinα）cosα＝0

∑Fξ＝0，ταd A＋（τd A cosα）cosα＋（τ＇d A sinα）sinα＝0

利用切应力互等定理，经整理后，即得任一斜截面ef上的正应力和切应力的计算公式分别为

由式（3.37）可知，单元体的四个侧面（分别为α＝0°和α＝90°）上的切应力绝对值最大，均等于τ。

由式（3.36）可知，在α＝－45°和α＝45°两斜截面上的正应力分别为

σ－45°＝σmax＝τ

σ45°＝σmin＝－τ

即该两截面上的正应力分别为σα中的最大值和最小值，即一为拉应力，另一为压应力，其绝对值都等于τ，且最大、最小正应力的作用面与最大切应力的作用面之间互成45°，如图3.36（d）所示。附带指出，这些结论是纯剪切应力的特点，并不限于等直圆轴在扭转时这一特殊情况。

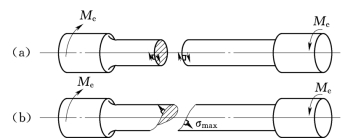
图3.37

在圆轴的扭转试验中，对于剪切强度低于拉伸强度的材料（例如低碳钢），破坏是从圆轴的最外层沿横截面发生剪断产生的[图3.37（a）]，而对于拉伸强度低于剪切强度的材料（例如铸铁），其破坏是由圆轴的最外层沿与杆轴线约成45°倾角的螺旋形曲面发生拉断产生的[图3.37（b）]。

3.圆轴扭转时的强度条件

圆轴受扭时，杆内各点均处于纯剪切应力状态。为了保证受扭圆轴能正常工作，不会因强度不足而破坏，应使圆轴内的最大工作切应力τmax不超过材料的许用切应力[τ]。即圆轴的强度条件为

由于等直圆轴的最大工作应力τmax发生在最大扭矩所在横截面（危险截面）的周边上任一点处，因此上述强度条件也可写成

对于变截面轴，如阶梯形轴、圆锥形杆等，由于Wt不是常量。所以，最大切应力τmax不一定发生在最大扭矩Tmax所在截面，这时要综合考虑T和Wt，求出的极值。上式中，[τ]为材料的扭转许用切应力，其值可查有关资料。实验指出，在静荷载作用下，材料的许用剪应力[τ]和许用拉应力[σ]之间存在有一定关系，对于塑性材料，[τ]＝（0.5～0.6）[σ]；对于脆性材料，[τ]＝（0.8～1.0）[σ]。

图3.38

【例3.7】 汽车传动轴简图如图3.38所示，转动时输入的力偶m＝1.6k N·m，轴由无缝钢管制成。外径D＝90mm，内径d＝84mm。已知许用切应力[τ]＝60MPa，许用单位扭转角[φ＇]＝0.026rad/m，材料剪切弹性模量G＝80GPa。①试校核轴的强度和刚度；②若改用强度相同的实心轴，试确定其直径，并比较两轴的重量。

解：（1）计算扭矩。由截面法可求得圆轴横截面上的扭矩为

T＝m＝1.6k N·m

（2）计算轴的抗扭截面模量和极惯性矩。

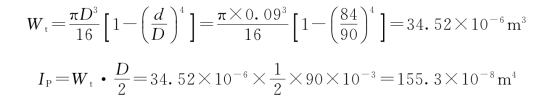
（3）校核轴的强度和刚度。轴的最大切应力为

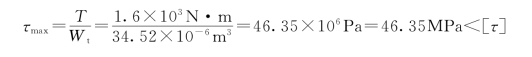
故轴满足强度条件。

轴的最大单位长度扭转角为

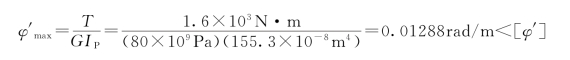
故轴满足刚度条件。

（4）确定改为实心轴的直径，并比较两轴用料。根据题意，实心轴的强度应和空心轴强度相同，故实心轴的最大切应力也应为45.5MPa，即

所以，改为实心轴的直径为

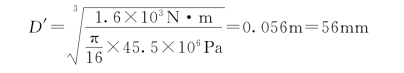
在两轴长度相等，材料相同的情况下，两轴重量之比又等于横截面面积之比。

空心轴的面积为

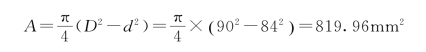
实心轴的面积为

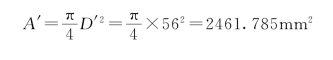
因此，两轴重量比为

由此可见，在强度相同的情况下，空心圆轴的自重比实心圆轴轻，即空心圆轴比实心圆轴省材料。

图3.39

【例3.8】 实心圆轴如图3.39（a）所示。已知该轴转速n＝300r/min，主动轮输入功率PC＝40k W，从动轮输出功率分别为PA＝10k W，PB＝12k W，PD＝18k W。材料的剪切弹性模量G＝80GPa，若[τ]＝50MPa，试按强度条件设计此轴的直径。

解：（1）首先计算外力偶矩。根据外力偶矩的计算公式（见第二章），求得

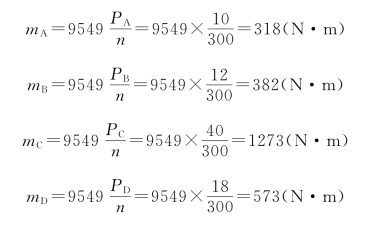
（2）计算扭矩并作扭矩图。由于外力偶矩将传动轴分为AB、BC和CD三段，故需分段使用截面法，计算各段横截面上的扭矩，即

AB段：　T1＝－mA＝－318N·m

BC段：　T2＝－mA－mB＝－318－382＝－700（N·m）

CD段：　T3＝mD＝573N·m

绘出扭矩图如图3.39（b）所示。由图可知，最大扭矩发生在BC段内，其值为

因该轴为等截面圆轴，所以危险截面为BC段内各横截面，其周边各点处切应力达到最大值。

（3）按强度条件设计轴的直径。由强度条件

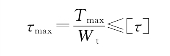
式中：，则