梁的内力图：剪力图和弯矩图

以梁横轴线作为横坐标（x轴），内力为纵坐标建立坐标系，画出剪力和弯矩沿梁轴线的变化图线，分别称为剪力图和弯矩图。

梁横截面上的剪力和弯矩随截面的变化规律可以由两种方法表示：一是内力方程；二是内力图。用内力图（几何法）表示内力沿轴线的变化规律较用内力方程（解析方法）表示内力沿轴线的变化规律，具有直观、形象之优点，并且由剪力图和弯矩图可以方便地确定梁中的最大剪力和弯矩及其所在截面的位置，这是进行强度、刚度分析的重要依据。

【例2.7】 图2.28（a）所示悬臂梁，在自由端受一集中力F作用，试作此梁的内力图。

解　为统一起见，均将梁的左端定为x轴的原点，坐标指向右。应用简便方法，直接写出距原点为x的任意横截面上的剪力和弯矩，便是梁的剪力方程和弯矩方程

然后根据方程做图。式（2.4）表明除端点外，整段梁各横截面上的剪力均为－F，所以剪力图线画在x轴的下方，图形为一水平直线，如图2.28（b）所示；式（2.5）表明弯矩是截面位置x的线性函数，自由端的弯矩值为零。无限靠近固端截面上的弯矩为：－Fl，所以图形是斜直线，根据弯矩正负号的规定，负号表示梁的中性层的上方纤维受拉，下方纤维受压，在画弯矩图时，我们规定，正的弯矩图画在下方、负的画在上方，不标正负。因此，在该题中，弯矩图画在x轴的上方，如图2.28（c）所示。另外，还可看出，无限靠近端部的剪力和弯矩值在数值上就等于端部约束反力和反力偶矩的数值。

图2.28

图2.29

【例2.8】 图2.29（a）所悬臂梁受集度为q的均布荷载作用，试作此梁的内力图。

解：运用简便方法，直接写出梁的剪力方程和弯矩方程

式（a）表明剪力沿截面线性变化，自由端的剪力为零，无限靠近固定端的横截面上的剪力为－ql，所以图形为一斜直线，如图2.29（b）所示。

式（b）表明弯矩沿截面按抛物线规律变化，自由端的弯矩为零，无限靠近固定端的横截面上的弯矩值为－ql2/2，弯矩图画在受拉一侧，不标正负，在该题中，梁的中性轴上方纤维受拉，所以，弯矩图画在x轴的上方，如图2.29（c）所示。

另外，还可看出，端部无集中力时，端部的剪力为零；端部无集中力偶时，端部的弯矩值为零。

【例2.9】 图2.30（a）所示简支梁受一集中力F作用，试作此梁的内力图。

解：先由梁的平衡条件求得支反力为

FA＝Fb/l

FB＝Fa/l

然后写出梁的内力方程：

第1段（AC），只看1—1截面左边的力，有

图2.30

第2段（BC），只看2—2截面右边的力，有

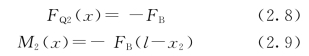
由式（2.6）和式（2.8）可知，两段剪力方程都是常数，图形都是水平直线，但1段在x轴的上方，2段在x轴的下方，如图2.30（b）所示。由式（2.7）和式（2.9）可知，两段弯矩都是x的线性函数，图形为斜率不同的斜直线；两端点处因无集中力偶，弯矩为零，分段点C处的弯矩值为ab F/l，所以用直线连接三个点便得弯矩图，如图2.30（c）所示。

从内力图可以看出，在集中力作用点，无限靠近的两侧横截面上剪力值不相等，即剪力图不连续而发生突变，突变跳跃值就等于集中力的数值，而弯矩图却是连续的。(www.xing528.com)

【例2.10】 图2.31（a）所示简支梁，受集度为q的均布荷载作用，试作此梁的内力图。

解：由平衡条件求得支座反力为

FA＝FB＝ql/2

写出距左端为x的任意横截面上的剪力和弯矩，得剪力方程和弯矩方程为

图2.31

式（a）表明各截面的剪力随x线性变化，图形呈斜直线，无限靠近两端截面上剪力的绝对值相等而符号相反，用直线连接两点便得剪力图，如图2.31（b）所示。

式（b）表明，弯矩图为抛物线，令弯矩方程关于x的一阶导数等于零，即

得极值点坐标

在极值点，弯矩的二阶导数为

表明有极大值

Mmax＝ql2/8

在两端点，弯矩值为零。用曲线连接两端点和极值点便得弯矩图，如图2.31（c）所示。从内力图可以看出，若梁的几何结构及受力对称，则弯矩图关于结构的对称轴对称。在弯矩的极值点处，剪力值力零；弯矩方程关于x的一阶导数等于剪力方程，这个结论具有普遍意义。

图2.32

【例2.11】 图2.32（a）所示简支梁，受一集中力偶M作用，力偶将梁分为两段，试作此梁的内力图。

解：由平衡方程求得支座反力为

FA＝M/l

FB＝－FA＝－M/l

分别写出两段梁的内力方程

第一段（AC段）

第二段（BC段）

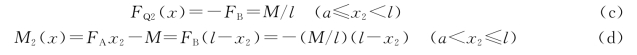
由式（a）和式（c）可以看出，两段的剪力方程为同一常数，所以两段图形为同一条水平直线。由式（b）和式（d）可知，两段的弯矩呈线性变化，图形为斜率相同的两条斜直线，两端点处弯矩为零，在集中力偶作用点无限靠近的两侧截面弯矩值不相同，即弯矩图不连续而发生突变，突变跳跃值就等于集中力偶矩的数值，而剪力图则是光滑的。