1.剪力与弯矩
梁受外力作用,其上各个截面将产生内力,内力由截面法根据平衡方程确定。如图2.22(a)所示简支梁,受一个集中力作用,支座反力FA、FB由平衡方程解得。沿任意横截面1—1截取左边部分研究,如图2.22(b)所示。横截面上的分布内力系向截面形心处简化得一主矢和一主矩。由于整体平衡,部分必定平衡,横截面上的主矢和主矩与外力形成平衡力系。因所有外力垂直于轴线,所以主矢也与外力平行,记为FQ,主矩与所有外力对横截面形心的力矩平衡,记为M,FQ和M就是梁的弯曲内力。因FQ在横截面内使梁沿横截面产生剪切错动的趋势,所以称为剪力。单位为N或k N;M使梁的横截面产生转动趋势而引起梁的弯曲,故称为弯矩,单位为N·m或k N·m。

图2.22
剪力与弯矩的正负号规定如下:
(1)剪力的正负:对于一段梁,其左侧截面的剪力向上为正、向下为负;右侧截面的剪力向下为正、向上为负。还可以解释为,使梁段顺时针转动的剪力为正,使梁段逆时针转动的剪力为负如图2.23(a)、(b)所示。
(2)弯矩的正负:对于一段梁,使梁段向下凸(下部受拉)的弯矩为正;使梁段向上凸(上部受拉的弯矩为负),如图2.24(a)、(b)所示。
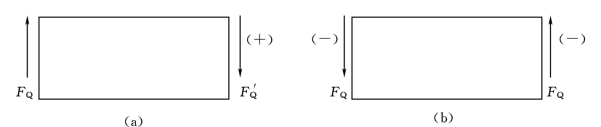
图2.23
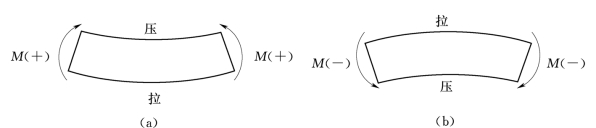
图2.24
【例2.4】 图2.25(a)所示悬臂梁,求指定横截面1—1、2—2上的剪力和弯矩。
解:(1)求支反力FA、MA。取全梁为研究对象,受力分析如图2.25(a)所示,列平衡方程:
由
∑Fy=0
FA-2aq-qa=0
得
FA=3qa
由
∑MA(F)=0
-qa2+6qa2+4qa2-MA=0
得
MA=9 qa2
(2)求指定截面的剪力和弯矩。沿1—1截面截取左边部分研究,受力分析如图2.25(b)所示,未知内力可假设为正,若求出的结果为正,说明与假设方向相同,内力就是正值;若求出的结果为负,说明与假设方向相反,内力就是负值。
由投影平衡方程
∑Fy=0
FA-FQ1=0
和对1—1截面形心的力矩平衡方程:
∑MC1(F)=0
-M1+FA a-MA=0
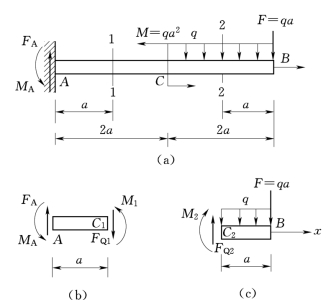
图2.25
求得1—1横截面的剪力和弯矩分别为
FQ1=FA=3qa
M1=FA a-MA=3qa2-9qa2=-6qa2
M1为负,说明与假设方向相反,实际应沿顺时针方向。
沿2—2截面截开,为方便计算,取右边部分研究,受力分析如图2.25(c)所示。由平衡方程:
∑Fy=0
FQ2-qa-qa=0
和
∑MC2(F)=0
-qa·a-qa·(a/2)-M2=0
得2—2截面上的剪力和弯矩
FQ2=2qa M2=![]()
2.剪力方程与弯矩方程
一般而言,梁横截面上的剪力与弯矩沿梁轴线是变化的,设沿梁轴线为x轴,则梁的剪力与弯矩是x的连续函数,记作:F(x)、M(x),分别称为剪力方程与弯矩方程。梁的内力沿轴线的变化规律可以用解析方法,也就是通过剪力方程与弯矩方程很好来表达。
【例2.5】 图2.26(a)所示简支梁,受两个集中力作用,此两力将梁分为三段,试求各段任意截面上的内力。

图2.26
解:(1)由梁的平衡条件求得支座反力为
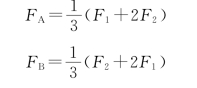
(2)用截面法求内力。在第1段中沿1—1截面截取左边部分为研究对象,受力分析如图2.26(b)所示。
由平衡方程: ∑Fy=0
FA-FQ1=0
和
∑MC1(F)=0
M1-FA x=0(https://www.xing528.com)
得第1段任意横截面上的内力
FQ1=FA (0<x<l/3)
M1=FA x (0≤x≤l/3)
对第2段,沿2—2截面截开,取左边部分研究,受力分析如图2.26(c)所示,由平衡方程:
∑Fy=0
FA-F1-FQ2=0
和
∑MC2(F)=0
M2+F1(x-l/3)-FA x=0
得第2段任意横截面上的内力
FQ2=FA-F1 (l/3<x<2l/3)
M2=FA x-F1(x-l/3) (l/3≤x≤2l/3)
对第3段,沿3—3截面截开,取右边部分研究,受力分析如图2.26(d)所示,由平衡方程:
∑Fy=0
FB+FQ3=0
和
∑MC3(F)=0
FB(l-x)-M3=0
得第3段任意横截面上的内力
FQ3=-FB (2l/3<x<l)
M3=FB(l-x) (2l/3≤x≤l)
【例2.6】 图2.27(a)所示简支梁,受一集中力偶作用,力偶将梁分成两段,试求各段任意横截面上的内力。
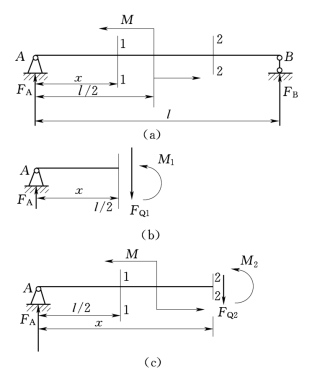
图2.27
解:1.求支座反力FA、FB
据图2.27(a)列平衡方程:
∑MB(F)=0
M-FA l=0
和
FA=M/l
因为力偶只能与力偶平衡,故FA、FB必构成力偶,所以
FB=-FA=-M/l
2.求内力
第1段:见图2.27(b),列平衡方程
∑Fy=0
FA-FQ1=0
∑MC1(F)=0
M1-FA x=0
得第1段任意横截面上的内力
FQ1=FA(0<x≤l/2)
M1=FA x(0≤x<l/2)
第2段:见图2.27(c),列平衡方程
∑Fy=0
FA-FQ2=0
∑MC2(F)=0
M+M2-FA x=0
得第2段任意横截面上的内力
FQ2=FA(l/2≤x<l)
M2=FA x-M(l/2<x≤l)
如果以2—2截面右边梁段上的外力来求内力,结果又会如何呢?请读者根据上述规律试试看。
从[例2.5]求三段内力的计算结果可以看出如下规律:
(1)任意横截面上的剪力在数值上等于该截面左侧或右侧梁段上所有外力的代数和。截面左侧梁段上向上的力或右侧梁段上向下的力在该截面产生正剪力,反之产生负剪力。
(2)任意横截面上的弯矩在数值上等于该截面左侧或右侧梁段上所有外力对截面形心之矩的代数和。向上的力产生正弯矩,向下的力产生负弯矩。
从[例2.6]还可以得出一个规律:
如果取截面的左边梁段研究,则顺时针转向的力偶在截面上产生正弯矩;取截面的右边梁段研究,则逆时针向的力偶在截面上产生正弯矩;反之产生负弯矩。
利用[例2.5]和[例2.6]归纳的三条规律,可以不必截取分离体和列平衡方程而直接写出任意截面的剪力和弯矩方程或求指定截面的剪力和弯矩值。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




