扭矩及其图示

1.扭矩

设一根等直圆截面轴，两端受扭力偶Me的作用，如图2.13（a）所示，用截面法求任意横截面上的内力。设一假想平面沿任意横截面m—m将轴截为两段，任取其中一段进行受力分析。因力偶只能与力偶平衡，所以横截面上的内力应是一个力偶[图2.13（b）]，该力偶的作用效果是使截面发生绕轴线的转动。所以称为扭矩，记为T，单位为k N·m。扭矩的大小由平衡条件确定。

沿轴线方向设x坐标，对轴线列力矩平衡方程

∑Mx＝0

T－Me＝0

T＝Me

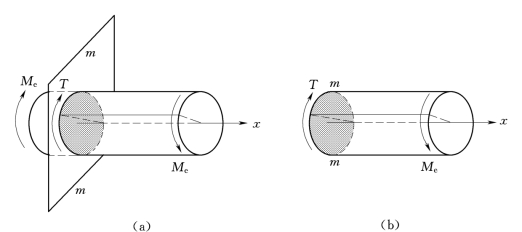
图2.13

扭矩的正、负规定：由右手螺旋法则判定，扭矩矢的指向与横截面的外法线方向一致时为正，反之为负。如图2.14（a）所示为正扭矩，而图2.14（b）所示为负扭矩。

图2.14

2.扭矩图

一般而言，轴各个横截面上的扭矩不同。为了讨论扭矩沿轴的轴线的变化规律及确定最大扭矩，通常用图形来表示，这种图称为扭矩图。

图2.15(www.xing528.com)

要绘制扭矩图，可建立T－x为坐标轴的直角坐标系，如图2.15（b）所示，x轴与圆轴的轴线平行，其值与各横截面的位置相对应，T轴垂直于x轴，其值是横截面上扭矩的代数值。扭矩图也可采用图2.15（c）的画法，正扭矩画在x轴的上方，负扭矩画在x轴的下方，无需画出T－x坐标轴。

【例2.3】 图2.16（a）所示传动轴，A轮为主动轮，其余为从动轮。已知转速n＝191r/min，各轮所传递的功率分别为PA＝20k W、PB＝PC＝6k W，PD＝8k W。试求各段的扭矩并作扭矩图。

解：作用于各轮的外力偶矩分别为

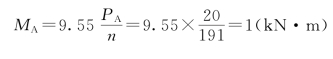
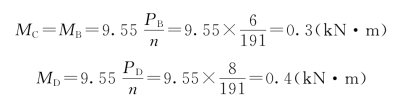
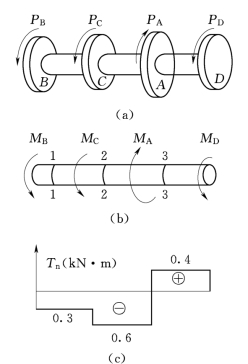
图2.16

轴的受力简图如图2.16（b）所示。

在每段轴内各取一个截面，并分别计算各截面的扭矩。

1—1截面扭矩的数值，等于截面一侧所有外力偶矩的代数和，现根据截面右侧的外力偶矩进行计算，其中MD使1—1截面处的轴段产生右螺旋变形，故使1—1截面上产生正扭矩；同样MC也为正扭距；相反，MA使1—1截面产生负扭矩，所以1—1截面的扭矩为

Mn1＝－MA＋MD＋MC＝－1＋0.3＋0.4＝－0.3（k N·m）

同理可得

Mn2＝－0.6k N·m

Mn3＝MD＝0.4k N·m

按比例画出扭矩图[图2.16（c）]。