当杆受多个力作用时,各段的轴力不同,如图2.8(a)所示,AB段的轴力与BC段的轴力不相同,求轴力时必须分段进行。
欲求AB段内某横截面m—m上的轴力,用截面法将杆沿m—m截开,设取左段为研究对象[图2.8(b)],以FN1代表该截面上的轴力。根据平衡条件:
∑Fx=0
FN1-F=0
FN1=F

图2.8
欲求BC段内某横截面n-n的轴力,则在n-n处截开,仍取左段研究[图2.8(c)],以FN2表示该截面的轴力,在不知FN2实际正负的情况下,可先假定为正。根据平衡条件:
∑Fx=0
FN2+2F-F=0
FN2=-F
计算结果为负号,表明FN2的实际方向与假设方向相反,即FN2为压力。
在多个力作用时,各段杆轴力的大小及正负号各异,如果选取一个坐标系,其横坐标表示横截面的位置,纵坐标表示相应截面的轴力,便可用图形表示轴力随截面位置的变化情况,该图形称为轴力图。轴力图的具体做法是:首先计算出各段的轴力,建立一直角坐标系,其中x轴与杆的轴线方向一致,表示杆横截面的位置,FN轴垂直于x轴,表示轴力的大小,通常坐标原点与杆端对应;再根据各段轴力大小绘出曲线,如图2.8(d)所示。
【例2.2】 试求图2.9(a)所示直杆各段截面的轴力,并绘制轴力图。
解:(1)求约束反力。解除约束A代之以反力FRA,取杆整体AD为研究对象图2.9(b),由平衡条件:
∑Fx=0
F1-F2-F3-FRA=0
FRA=F1-F2-F3=18-8-4=6(k N)
(2)计算各段的轴力。
1)计算AB段的轴力。在AB段内沿1—1截面假想将杆截开,取左段为研究对象,设该截面上的轴力FN1为拉力[图2.9(c)],由平衡条件:
∑Fx=0
FN1-FRA=0(https://www.xing528.com)
FN1=FRA=6k N
结果为正,表明FNl的实际方向与所设方向一致。
2)计算BC段的轴力。在BC段内沿2—2截面假想将杆截开,仍取左段为研究对象,并设该截面上的轴力FN2也为拉力[图2.9(d)],由平衡条件:
∑Fx=0
FN2-FRA+F1=0
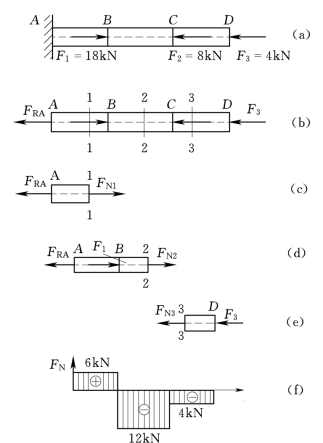
图2.9
FN2=FRA-F1=6-18=-12(k N)
结果为负,表明FN2的实际方向与所设方向相反,FN2为压力。
3)计算CD段的轴力。在CD段内沿3—3截面假想将杆截开,取右段为研究对象,并设该截面上的轴力FN3也为拉力[图2.9(e)],由平衡条件:
∑Fx=0
-F3-FN3=0
FN3=-F3=-4k N
结果为负,表明FN3的实际方向与所设方向相反,为压力。
(3)画轴力图。按前述方法,取适当比例绘出轴力图如图2.9(f)所示。
由图可见,各段的轴力不同,但每段的轴力图为水平线,这表明段内各截面的轴力相等。杆中最大轴力(绝对值)产生在BC段,其值为
|FN|max=12k N
由此例可见:
(1)应用截面法求轴力时,如果都假设截面上的轴力为正,则由平衡方程求出轴力的正、负号既表明该轴力的实际方向与所设方向之异同。又准确反映该轴力的拉、压性质。
(2)在应用截面法求轴力时,选取外力较少的一段作为研究对象,可减少计算量。
(3)求杆件轴力还可以不用截面法,而是用下面简便的口角进行计算。口角:“杆件某一截面上的轴力等于该截面以左(或以右)杆件所受到的所有轴向外力的代数和,以左部分向左外力取正(以右部分向右的外力取正),反之取负”。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




