杆件轴力的分析与计算

可以看出，上述轴向拉伸（压缩）的杆件（简称为拉压杆）虽然端部的连接情况或传力方式各不相同，但它们受力的共同特点是：杆上的外力作用线与杆的轴线重合。在这种外力作用下，杆件的变形特点是：杆件只沿轴线伸长或缩短[图2.6（a）、（b）]。

图2.7（a）所示一受轴向外力拉伸的杆件。欲求杆某一横截面m—m上的内力，用截面法将杆件沿该截面切开，取左段为研究对象。根据平衡条件，截面m—m上的分布力系应与F平衡，设分布力的合力为FN[图2.7（b）]，它与F构成二力平衡关系，必与杆的轴线重合，故称该合力为轴力。

图2.6

根据平衡方程：

∑Fx＝0

FN－F＝0

FN＝F

上式表达了杆件某截面上的轴力FN与杆件所受外力的关系。(www.xing528.com)

如果以右段为研究对象[图2.7（c）]，按上述过程进行类似的处理，也可求得m—m截面上的轴力为

∑Fx＝0

FN＇－F＝0

FN＇＝F

即轴力FN＇的大小也等于F，方向与FN相反，作用线沿杆轴线。由此可见，用截面法求内力时，无论取哪一部分为研究对象，所求得的内力数值完全相同，但方向相反。这很显然，因为它们是作用力与反作用力的关系。为保证取不同部分为研究对象能得到唯一的计算结果，材料力学以变形来确定内力的正负号，规定：使杆件产生拉伸变形的轴力为正；使杆件产生压缩变形的轴力为负。

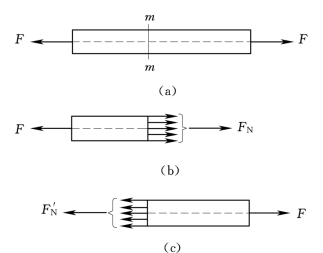
图2.7

根据这个规定，轴力方向背离截面为正，指向截面为负。图2.7（b）、（c）上分别表示的FN和F＇N虽然方向相反，但同为拉力，均为正号。