10.1 实验目的
图10.1 开口薄壁梁实验装置
根据开口薄壁梁实验装置，完成以下项目（或选做其中几项）。自行设计试验方案、根据试验方案确定贴片位置、组桥和加载方式等。
（1）测定载荷作用于各种位置时，翼缘上下外表面中点的扭转切应力。
（2）测定载荷作用于各种位置时，翼缘上下外表面两边缘处的弯曲正应力。
（3）用实验数据说明本实验装置的固定端约束对弯曲正应力的局部影响范围。
（4）用实验数据说明本实验装置的固定端约束对扭转切应力的局部影响范围。
（5）用实验数据说明圣维南原理的影响范围。
10.2 实验设备和仪器
（1）开口薄壁梁实验装置（图10.1）。
10.3 实验原理
约束扭转既然引起横截面上的正应力而相邻横截面上的正应力又不相等，故又将引起附加剪应力。约束扭转杆件截面的应力由两部分组成：扭转剪应力组成的力偶矩为Mn，附加剪应力组成的力偶矩为Mw则两者的总和应与外力的力偶矩Mz平衡，Mz＝Mn＋Mω。
实验装置为槽形截面的悬臂梁，其一端固定，自由端施加集中力F，但由于集中力并没有通过截面的扭转中心，现将集中力向扭转中心平移后，将会附加产生一个扭转力偶矩M＝Fa。理论计算简图如图10.2所示。
图10.2 理论计算简图
取悬臂梁的固定端为坐标原点，根据固定端的边界条件和静力平衡条件，已知的初参数有：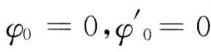
，M0＝M。
可求出约束扭转力偶矩为：
自由扭转力偶矩为：
10.3.1 弯曲正应力(www.xing528.com)
约束扭转双力矩产生的正应力为：
平面弯曲产生的正应力为：
10.3.2 弯曲剪应力
约束扭转产生的剪应力为：
考虑约束扭转的自由扭转产生的剪应力为：
10.3.3 弯曲切应力
弯曲产生的切应力为：
10.4 实验报告
实验报告的主要内容包括：
（1）设计实验方案。
（2）设计实验原始数据表格并完成记录。
（3）实验数据分析和结论。
（4）分析弯曲正应力受固定端处的约束双力矩的影响的大小和范围。
（5）根据实验结果说明开口薄壁结构中圣维南原理的适用范围，在类似的结构设计中应注意什么问题，特别是在对于开口薄壁的钢结构的设计问题。
10.5 开口薄壁杆件的物理特性和截面的几何特征值
截面形状为槽形，见图10.3。
图10.3 横截面示意图
尺寸为：长l＝300mm，宽b＝22mm，高h＝44mm，厚度t＝4mm。
表10.1 开口薄壁杆件的物理特性和截面的几何特征值
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
