深入探究弯曲时正应力分布的实验

7.1 实验目的

（1）测定梁纯弯曲时的正应力分布规律，并与理论计算结果进行比较。

（2）熟练应用电测的基本方法进行应变测试。

7.2 实验设备

（1）纯弯曲梁实验装置。

（2）静态电阻应变仪。

（3）矩形截面梁。

7.3 实验原理

试样采用低碳钢制成的矩形截面梁，加载方式如图7.1所示。在梁AB承受纯弯曲变形的CD的某一截面上，根据梁的高度h，每隔h/4贴上平行于轴线方向电阻应变计。其中R6和R7分别贴在梁的上、下边缘，R8在梁的底部沿垂直轴线方向粘贴，R2、R3分别粘贴在上、下h/4的位置，R1粘贴在h/2的位置上。当梁弯曲时，即可测出各点处的轴向应变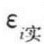（i＝1、2、3、4、5、6、7、8）。由于梁的各层纤维之间无挤压，根据单向应力状态的胡克定律，求出各点的实验应力为：

图7.1 矩形截面梁

梁纯弯曲时的正应力公式为：

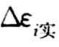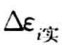实验采用增量法加载。根据钢梁的强度和力传感器的量程估算最大实验荷载Fmax。根据钢梁的强度计算，Fmax应按钢梁最大弯曲正应力与钢梁材料的许用应力进行校核，即；再根据力传感器的量程考虑，一般按力传感器的标称最大承受荷载确定；最后取两者计算结果的较小值确定Fmax。选取适当的初荷载F0，一般为Fmax的10％左右。由F0至Fmax可分成四级或五级加载，每增加等量的载荷ΔF，测得各点相应的应变增量为，求出的平均值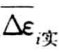，依次求出各点的应力增量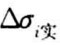为：

根据公式（6.1）计算各点应力增量的理论值为：

式中：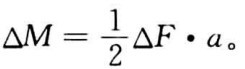

将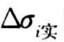的数据与的理论计算结果进行比较，验证理论公式的正确性。

根据R7和R8应变计测得的数据，计算横向变形系数为：

7.4 实验步骤

（1）根据低碳钢的许用应力和力传感器的量程确定最大实验荷载，并根据该荷载确定每次加载的增量。

（2）分别将各测点的工作应变计、补偿应变计接入电阻应变仪，预调平衡。(www.xing528.com)

（3）请指导教师检查后，开始预加载，检查加载设备和应变仪是否处于正常工作状态。

（4）测试时要缓慢加载，记下每次荷载的增量ΔF和相应的应变增量Δε；注意应变是否按比例增长，每个测点加载后卸载，重复三次。重复加载中出现的误差大小，可表明测量的重复性，测试结果可靠程度。测完一点再换另一点，直至全部测完。

（5）小心操作，应特别注意不要超载，最大荷载不得超过5kN。

（6）实验结束后，应将导线从电阻应变仪上拆除，整理好放回原处。

7.5 实验结果的处理

（1）根据实验数据，逐点算出应变增量平均值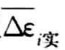，代入公式（7.2）求出。

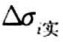（2）根据公式（7.3）计算各点弯曲正应力的理论值。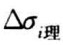

（3）实验值与理论值进行比较，计算相对误差。

（4）绘制应变与梁高的分布曲线，验证是否存在中性轴，根据各点的应变数据计算中性轴位置；分析纯弯曲正应变分布是否满足平截面假定，由此推断当材料在线弹性范围时应力分布的情况。

（5）根据公式（7.4）计算钢梁的横向变形系数μ

7.6 思考题

（1）实验结果和理论计算是否一致？如不一致，其主要影响因素是什么？

（2）弯曲正应力的大小是否受弹性模量E的影响，如果材料的拉伸时的E＋和压缩时的E﹣不相同时又会怎样？

（3）在增量法测量中，未考虑梁的自重，是不是应该考虑？还是忽略不计？

（4）如果测量钢梁的横向变形系数μ非常接近钢梁的实际横向变形系数0.28，这说明什么？

（5）如何根据实验结果计算出实测中性轴的位置，中性轴是否一定过横截面的形心？

（6）若低碳钢的许用应力[σ]＝170MPa，则弯曲实验装置中的钢梁能承受的最大荷载是多少？为什么实验用的弯曲实验装置的最大荷载是5kN？