电阻应变计测量原理实验详解

5.1 实验目的

（1）掌握电阻应变计测量应变的原理。

（2）了解电阻应变仪的工作原理，掌握电阻应变仪的操作方法。

（3）熟悉测量电桥的应用，掌握在测量电桥中的各种接线方法。

5.2 实验设备

等强度梁实验装置；数字式电阻应变仪。

5.3 实验装置及原理

5.3.1 电阻应变计的工作原理

电阻应变计习惯称为电阻应变片，是最常用的力学量传感元件。用应变片测试时，应变片要牢固地粘贴在测试体表面。当测件受力而发生变形时，应变片的敏感栅随同变形，其电阻值也相应发生变化，这种现象称为金属的电阻应变效应。通过测量电路将其转换成电信号输出。长度为l、截面积为S、电阻率为ρ的匀质金属丝，其电阻值为R＝ρl/S，等式两边取微分，得：

式中：——电阻的相对变化；

电阻率的相对变化；

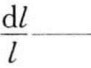金属丝长度相对变化，且ε＝dl/l称为金属丝长度方向上的应变或轴向应变，

截面积的相对变化。

若金属丝的直径为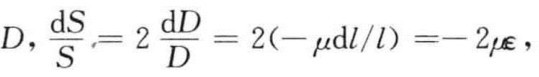则有：

上式表明，金属丝受力变形后，由于其几何尺寸和电阻率发生变化，从而使其电阻随之发生变化。可以设想：若将一根金属丝粘贴在构件表面上，当构件变形后，金属丝也将随之变形，利用金属丝的应变-电阻效应就可以将构件表面的应变量转化为电阻的相对变化量。电阻应变计就是利用该原理制成的应变敏感元件。试验表明，金属丝电阻的相对变化与金属丝在弹性范围内应变量之间存在线性关系。

若令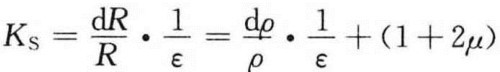，则有：

比例系数Ks称为应变计的灵敏系数（单位应变引起的电阻相对变化），它表明应变计对承受的应变量的灵敏程度。这一系数不仅与敏感栅材料的泊松比有关，并且与敏感栅变形后电阻率的相对变化有关。

5.3.2 测量电桥的基本特性

惠斯登电桥是最常用的非电量测量电路之一，习惯称为测量电桥，如图5.1所示。测量电桥以电阻应变计作为桥臂组成电桥电路，将应变计的电阻变化转化为电压或电流信号。

图5.1 惠斯登电桥

ABC间流过的电流为：

由此得到R1两端的电压降为：

同理R4两端的电压降为：

可以得到电桥输出电压为：

由上式可知，要使电桥平衡，应使电桥输出电压UBD为零，则桥臂电阻必须满足：

R1R3＝R2R4 　（5.5）

当各桥臂电阻发生变化时，电桥就有输出电压。设各桥臂电阻相应发生了ΔR1、ΔR2、ΔR3、ΔR4的变化，则由公式（5.4）得到电桥的输出电压为：

将公式（5.5）代入上式，由于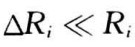，可略去高阶微量。故可得：

公式（5.6）（5.7）分别是电桥输出电压的精确计算公式和近似计算公式。

若电桥的四个桥臂上均为应变计，且假设阻值相等，即R1＝R2＝R3＝R1＝R，则公式（5.7）为：

如果电阻应变计的灵敏系数KS相同，将ΔR/R＝KSε代入公式（5.8），便可得到电桥的输出电压：

式中：ε1为AB桥臂应变计感受的应变；

ε2为BC桥臂应变计感受的应变；

ε3为CD桥臂应变计感受的应变；

ε4为DA桥臂应变计感受的应变。应变仪上的读数通常对应于读数应变εd，而不是电桥电压输出UBD，因此上式可变为：

εd＝ε1－ε2＋ε3－ε4 　（5.10）

由上式可见，测量电桥有如下特性：

（1）两相邻桥臂上应变计所感受的应变，代数值相减；

（2）两相对桥臂上应变计所感受的应变，代数值相加。

在应变电测中，合理地、巧妙地利用测量电桥的特性，可以实现如下测量：

（1）消除测量时环境温度变化引起的误差；

（2）增大应变读数，提高测试灵敏度；

（3）通过合理的组桥方法，可以测出复杂受力杆件中的某一内力分量。

应用公式（5.10）时应注意，应变仪上的灵敏系数设置与应变计的灵敏系数一致时，测量得到读数应变εd即为被测件表面的应变，若两者不一致，则需要进行修正，修正公式为：

式中：ε——被测件表面应变；

K仪——应变仪灵敏系数；

Ks——应变计灵敏系数。

5.3.3 电阻应变计在测量电桥中的接线方法

应变计在测量电桥中有各种接法。实际测量时，根据电桥基本特性和不同的使用情况，采用不同的接线方法，以达到以下目的：①实现温度补偿；②从受力复杂的构件中测出所需要的某一应变分量；③提高被测物体应变的读数，提高测量的灵敏度。为了达到上述目的，需要充分利用电桥的基本特性，精心设计应变计在电桥中的接法。

在测量电桥中，根据不同的使用情况，各桥臂的电阻可以部分或全部是应变计。测量时，应变计在电桥中，常采用以下几种接线方法：

1）单臂接线法

若在测量电桥的桥臂AB上接电阻应变计，而另外三个桥臂BC、CD和DA接固定的标准电阻，则称为单臂接线法（常称为1/4桥），见图5.2。此接法无温度补偿作用，仅仅适用于瞬态信号的测试。

图5.2 单臂接线法（1/4桥）

2）半桥接线法

测量电桥中R1、R2两桥臂电阻为电阻应变计，R3、R4两桥臂电阻为固定电阻，该连接方式称为半桥接线法。

（1）单臂半桥接线法

在构件被测点处粘贴电阻应变计，称工作应变计（简称工作片），接入电桥的AB桥臂；另外在补偿块上粘贴一个与工作应变计规格相同的电阻应变计，称温度补偿应变计（简称补偿片），接入电桥的BC桥臂；在电桥的CD和DA桥臂上接入固定电阻（或者为标准电阻）。这种接线方法称为单臂半桥接线法（常称为半桥外补偿法），见图5.3。

图5.3 单臂半桥接线法

图5.4 温度补偿

粘贴在被测件上的电阻应变计，其敏感栅的电阻值一方面随被测件的应变而变化，另一方面，当环境温度变化时，敏感栅的电阻值还将随温度改变而变化，同时，由于敏感栅材料和被测件材料的线膨胀系数不同，敏感栅有被迫拉长或缩短的趋势，也会使其电阻值发生变化。这样，通过应变片测量出的应变值中包含了环境温度变化而引起的应变，造成测量误差。因此需要准备一个材料与被测构件相同且不受外力的补偿块，在其上粘贴温度补偿片，使补偿片与工作片处于同一温度场中，以消除环境温度变化而引起的应变测量误差见图5.4。需要注意的是，温度补偿片应满足下四个条件：

①AB桥臂和BC桥臂上的应变计必须属于同一批号的，即它们的电阻值、电阻温度系数α、线膨胀系数β、应变灵敏系数Ks都相同；

②用于粘贴补偿片的补偿块和粘贴工作片的试件的材料必须相同，并且不受外力作用；

③两个应变计处于同一温度环境中；

④两个应变计粘贴的工艺要相同。

在应变测量过程中，工作片直接感受构件受力后的应变ε和环境温度变化产生的应变εt；补偿片将只感受环境温度变化产生的应变εt。

由公式（5.10）可得读数应变：

εd＝ε1－ε2＝ε＋εt－εt＝ε

读数应变等于构件上被测点的应变ε，该接线方法实现了消除环境温度变化引起的应变读数误差。

图5.5 双臂半桥接线法

图5.6 悬臂梁

（2）双臂半桥接线法

接入AB桥臂和BC桥臂电阻应变计均为工作应变计，均粘贴在被测试样上，见图5.5。当试件受力且测点环境温度变化时，每个应变计的应变中都包含外力和温度变化引起的应变，根据电桥基本特性，在应变仪的读数应变中能消除温度变化所引起的应变，从而得到所需测量的应变，这种方法叫工作片补偿法（常称为半桥自补偿法）。应用双臂半桥接线法，一方面可消除环境温度变化引起的误差，另一方面还可以增加读数应变，提高测量灵敏度。

如图5.6所示一悬臂梁，在Ⅰ-Ⅰ截面上、下表面各粘贴一片应变计。在F力作用下，Ⅰ-Ⅰ截面上、下表面的应变ε大小相等，符号相反。用双臂半桥接线法，两桥臂的应变计感受梁在F力作用下的应变ε和环境温度变化产生的应变ε，分别为：

ε1＝ε＋εt，ε2＝﹣ε＋εt(www.xing528.com)

由公式（5.10）得读数应变εd为：

εd＝ε1－ε2＝ε＋εt－（﹣ε＋εt）＝2ε

读数应变εd是悬臂梁Ⅰ-Ⅰ截面处应变的两倍。所以，双臂半桥接线法消除了环境温度变化引起的误差，也增加了读数应变，提高了测量灵敏度。

3）全桥接线法

在测量电桥的四个桥臂上全部接电阻应变计，称为全桥接线法，见图5.7和5.8。根据四个应变计工作情况的不同，又分为对臂全桥接线法和四臂全桥接线法。

（1）对臂全桥接线法

测量电桥中R1、R2、R3、R4四桥臂应变计中R1、R3为工作应变计，R2、R4为补偿应变计，即R1、R3应变计粘贴在被测构件上，R2、R4应变计粘贴在补偿块上（反之R2、R4作为工作应变计，R1、R3应变计作为补偿应变计也可以）。

如图5.7（a）所示等强度梁，要测定在力F作用下等强度梁上产生的轴向应变εF。

在等强度梁上同一截面的正、反两面各粘贴一片轴向应变计，同时在与等强度梁相同材料的补偿块上也粘贴两片应变片，见图5.7（b），并用对臂全桥接线法组成图5.7（c）所示测量电桥。四桥臂应变计感受的应变分别为：

ε1＝ε3＝εF＋εt，ε2＝ε4＝εt

由公式（5.10）可得读数应变εd为：

εd＝ε1－ε2＋ε3－ε4＝（εF＋εt）－εt＋（εF＋εt）－εt＝2εF

此时等强度梁的轴向应变

图5.7 对臂全桥接线法

（2）四臂全桥接线法

测量电桥中R1、R2、R3、R4四桥臂应变计均为工作应变计。

仍以测量图5.8所示等强度梁在F作用下的轴向应变εF为例。在等强度梁的两个截面正、反两面，沿轴线方向粘贴应变计，见图5.8，并用四臂全桥接线法组成图5.8测量电路。四桥臂应变计感受的应变分别为：

图5.8 四臂全桥接线法

ε1＝ε3＝εF＋εt

ε2＝ε4＝﹣εF＋εt

由公式（5.10）可得读数应变εd为：

εd＝ε1－ε2＋ε3－ε4＝（εF＋εt）－（﹣εF＋εt）＋（εF＋εt）－（﹣εF＋εt）＝4εF

此时等强度梁的轴向应变

无论是对臂全桥接线法还是四臂全桥接线法组成的测量电桥，都消除了环境温度变化引起的误差，而且增加了读数应变，提高了测量灵敏度，最大放大倍数可以达到4倍。

4）串并联接线法

在应变测量中，也可以将应变计串联或并联起来接入测量桥臂，如图5.9和图5.10所示。

图5.9 串联双臂接线法

图5.10 并联双臂接线法

（1）串联时桥臂应变的计算

设AB桥臂中串联了n个阻值为R的电阻应变计，则该桥臂的总电阻阻值为nR。当每个应变计的电阻变化为时，则：

串联后桥臂感受的应变为各个应变计感受应变的算术平均值。当每个桥臂中串联的各个应变计感受的应变相同时，即时，则：

ε1＝ε′

这说明串联接线不会增加读数应变，不能提高测量灵敏度。

（2）并联时桥臂应变的计算

先推导并联电阻的变化与等效电阻变化的关系，以及单个电阻应变计的应变变化与等效电阻的等效应变变化的关系。

设n个电阻R1、R2、⋯、Rn并联，其等效电阻为R，则有：

等式两边同时取全微分，有：

如果R1、R2、⋯⋯、Rn都等于R0，则等效电阻R＝R0/n，有：

整理得：

所以：

可见，阻值相同的应变计并联时，总等效电阻的等效应变为各个应变计应变变化的平均值。

所以，并联接线也不能提高读数应变，不能提高测量灵敏度。

通过对以上各种接线方式的分析可以看出，采用不同的接桥方式，所得的读数应变是不同的，即电桥的测量灵敏度是不同的。因此，测量电桥实际应用时，应根据具体情况灵活应用。

5.3.4 等强度梁

等强度梁如图5.11所示，梁的外形为等腰三角形，集中力F作用在三角形顶点。梁各横截面的最大正应力是相等的，因此称为等应力梁，因此梁上、下表面上各点的沿着轴线方向的应变也相等，其应变为：

图5.11 等强度梁及电阻应变计贴片位置示意图

式中：F为荷载，l为梁的长度，b为梁固定端处的宽度，t为梁的厚度，E为等强度梁材料的弹性模量。

在等强度梁上、下表面分别粘贴3个应变计，共6个应变计；其中4个沿梁的轴线方向粘贴，中间2个垂直于梁的轴线方向粘贴。根据等强度梁的特性，4个沿轴线方向粘贴应变计的读数绝对值应相同，符号根据贴片的位置确定。2个垂直于梁的轴线方向粘贴应变计的读数绝对值也相同，但与沿梁的轴线方向粘贴应变计的读数相比是不同的，两者绝对值之间的比值应是材料的横向变形系数（泊松比）。6个应变计可以按不同的接线方法进行组合，不同的组合产生的应变读数可能不同，也可能相同，需要自行设计。通过设计不同接线方法，掌握各种电桥接线方法应变输出的规律。

5.4 实验步骤

（1）记录试件编号、尺寸和参数。

（2）选择合适接线方案，一般选择单臂半桥接线法、双臂半桥接线法、四臂全桥接线法。

（3）根据选定接线方案，绘制接线电路简图，计算输出应变。

（4）检查接线、试加载，检查仪器工作是否正常。

（5）正式加载前，记录下电阻应变仪的初始读数或将读数调零。

（6）每加载一次记录一次应变仪的读数，每个接线方案测试至少重复3次。

（7）加载完成后整理和检查数据。

（8）关闭电源，拆下导线并整理设备。

5.5 实验结果处理

（1）数据处理，计算出以上各种测量方法下，ΔF所引起的应变的平均值Δεd，并计算它们与理论值的相对误差。

（2）比较各种测量接线法电路的测量输出应变的关系，并分析各种测量方法中温度补偿的实现方法。

（3）对几组实验数据求平均值、标准差与不确定度。

5.6 思考题

（1）试述电阻应变计的工作原理。

（2）什么是应变计的灵敏系数？怎样进行标定？

（3）用加长或增加栅线数的方法改变应变计敏感栅的电阻值，是否能改变应变计的灵敏系数？为什么？

（4）应变计测量的应变是下述三种情况中的哪一种？

①栅长中心点处的应变；②栅长长度内的平均应变；③栅长两端点处的平均应变。

（5）有一粘贴在简单拉伸试件上的应变计，其阻值为120Ω，灵敏系数K＝2.12。问试件上应变读数为﹢1000με时，应变计的阻值是多少？如果试件上应变读数为﹣1000με时，应变计的阻值又是多少？

（6）电阻应变计达到完全补偿的必要条件有哪些？测量电桥的特性有哪些？试述测试误差与接线方法的关系。

（7）分析各种测量接线法中温度补偿的实现方法。

（8）采用串联或并联接线法能否提高测量灵敏度？

（9）应变仪设置的灵敏系数K仪和应变计的灵敏系数K片不一致时，应变数据如何修正？