Al颗粒燃烧的微米级和纳米级普适性规律：基于扩散理论的动力学研究

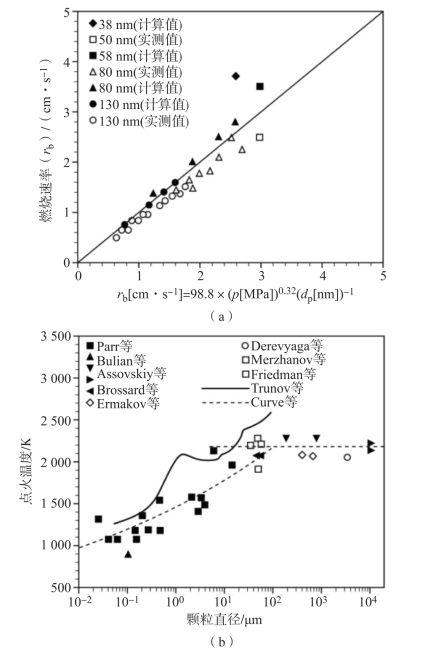
图5.2　（a）在不同粒径和压力下测量和计算的燃烧速率以及（b）氧气环境中铝颗粒的点火温度与颗粒直径的函数关系［HUA 09］（版权2009，爱思唯尔出版集团）

图5.2（a）所示为实验测量的铝颗粒燃烧速率（rb），以及点火温度与颗粒直径的函数关系［HUA 09，SUN 13］。图5.2（a）记录的数据是有关浸入水燃烧体系的，重点是粒度和压力对燃烧反应的影响。Sundaram等认为燃烧速率与粒径成反比，图5.2（b）显示出不同条件与粒度分布下的数据［SUN 13］，在比较和分析这些数据时需要特别小心。总的趋势表明，直径较大的铝颗粒（＞100μm），点火温度接近氧化铝的熔点（即2 070℃）。对于纳米铝颗粒，目前报道的反应温度接近铝的熔点（660℃）。

Brooks等最近做了相关研究的详细综述［BRO 95］。本章概括总结了主要的研究趋势和结论。因为温度可以测量，所有的论文均假定铝颗粒完全燃烧。此外，气相中不含固态气溶胶颗粒，燃烧时间tb与Al颗粒直径d遵从指数（n）幂律关系：(www.xing528.com)

经典火焰扩散理论认为n＝2，即tb～d2，而动力学控制理论则认为n＝1，即tb～d。对于微米铝颗粒的燃烧反应来说，由于氧化物钝化层的存在，指数n小于2（即tb～dn，其中n＜2）。Brooks等通过拟合实验数据认为n等于1.8［BRO 95］。我们也注明当颗粒直径大于10μm时，燃烧时间主要是环境气体温度的函数，此时n减小到0.5。Bazyn等认为，对于微米铝颗粒来说，必须分别考虑氧化气氛和燃烧条件的影响，例如O2和CO2的百分比，因此，指数n介于0.68～1.15之间［BAZ 07］。Huang等认为直径在100 nm左右的纳米铝颗粒，指数n＝0.3［HUA 07］。此外他们还发现，通过改变氧化气氛中的氩气量，火焰温度可以控制在630～2 100℃。

Rai等通过等式t∝d1.6±0.1（直径＜35 nm）来表征纳米铝颗粒的燃烧时间，其中t是颗粒反应所需的时间，d是颗粒直径［RAI 06］。这个规律表明，如果只考虑核收缩模型，大颗粒反应快于小颗粒。如果这个过程仅仅是自由分子状态下颗粒的表面反应，那么d和t可能呈线性关系。如果只考虑铝的扩散或者只考虑氧通过氧化物外壳的扩散，那么就没有任何压力梯度，则可得到t∝d2。因为只涉及铝核的熔化，所以这与忽略压力梯度下的核收缩模型［LEV 99］一致。