缓慢加热条件下铝氧化热力学模型分析

在实验层面，通过组合几种技术共同探索氧化的热力学。例如已经提及的，使用TGA分析在O2／Ar（25／75）环境中由室温到1 300℃表征氧化过程。TGA曲线给出了由氧化过程产生的质量增加，并且可以添加同步DSC测量以量化相应的放热效应以及相变检测。也可以通过X射线衍射或拉曼分析热处理检查前后粉末的结构和性质。这些实验结果［JOH 07，MEN 98b，JON 00］通常彼此一致，并且显示对于100 nm和更细的颗粒，氧化反应大部分发生在铝熔点以下，450～605℃之间，并且有比宏观尺度的铝粉更高的反应度。

由于纳米铝粉氧化速率的内在机理至今未有清晰的认知，因此关于实验结果的解释分析中不可避免存在争议。一些人提出，铝核膨胀和破裂，高速喷射出熔融的金属铝团簇。另外一些人认为，铝核的铝和外表面的氧原子扩散而后在钝化层内发生反应，这将在后续第5章中进行更详细的讨论和综述。

1.4.2.1　恒定点火温度模型

文献中发现的最简单的第一点火模型基于许多实验，结果显示大的铝颗粒（直径＞10μm）在接近Al2O3的熔点（即2 042℃）处点火［BOI 02，BRO 95］。该模型认为存在于铝表面上的氧化物膜一直阻碍点火，直到其开始熔化，熔化形成孤立的氧化物区域取代之前的连续钝化层。于是铝暴露于氧化剂中，颗粒发生点火，因此，这种模型描述铝点火的基本假设是铝点火温度始终恒定。目前业内的统一认知是，将点火温度选择为稍低于密实状态Al2O3熔点，即认为薄且生长受限的保护性氧化层熔点低于宏观氧化铝，则与实验数据具有更好的一致性。对于使用大颗粒铝粉（超过微米尺寸）的实验，该模型产生相当令人满意的结果，然而这种方法不适于更细的铝颗粒。

1.4.2.2　氧化层内部压力模型

这个模型是由Rozenband［ROZ 92］等提出的，认为保护性氧化物层在加热期间由于内核铝熔融积累机械应力而破裂。铝表面暴露在氧化剂中随之发生颗粒点火。这一假设被广泛讨论：对被加热氧化铝的力学性能知之甚少，氧化膜中最大应力产生于铝熔化即将迸裂的时刻，也就是温度高于600℃的瞬间。在温度升高超出1 100℃时，Al2O3的相变导致晶界滑动，发生脆性至延性转变。因此，可以中和氧化膜中的应力，避免氧化膜破裂。该模型有争议之处在于，无法恰当描述低温状态（500～600℃）下观察到的铝粉点火。

1.4.2.3　氧化生长模型

氧化生长动力学模型建立的常规方法是假定遵从线性抛物线方程，该方法认为初始生长过程由气相环境中的氧化性物质与铝之间的化学反应控制，总氧化可以写成如下形式［FED 03］：

式中，toxide为氧化层厚度；t为时间；Cm ox为氧化剂浓度，与颗粒表面附近氧化性气体压力成正比；m为与氧化剂相关的反应级数；R为通用气体常数；E和K分别为活化能和指前因子。指数n决定了氧化速率对氧化层厚度的依赖关系，n＝0时为线性氧化定律（适用于第一阶段氧化），n＝1时为抛物线定律，描述氧化性物质通过之前反应生成氧化物的扩散，从而发生氧化反应的动力学方程。

在另外的公式中，通常氧化机理方程可以被表述成无量纲形式：

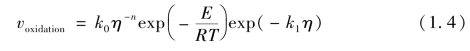
式中，voxidation为反应速率；η为氧化程度，通过TGA的质量变化确定；k0为指前因子；E为化学反应氧化的活化能；R为通用气体常数；T为反应温度；n和k1分别为指数和系数常数；E和k1为独立变量。通常，这些值是从铝氧化实验研究中得到的，活化能通常不取决于粒度，铝氧化活化能平均值约为155 kJ／mol，文献中查询到异相铝氧化活化能为70～420 kJ／mol，数值大小与温度范围相关。例如在［TRU 06］中，Trunov等报道的活化能在950～1 300℃范围时为460 kJ／mol，1 600～2 000℃温度范围时为71 kJ／mol。发现纳米粉末k0比大尺寸粉末高出2～5倍。在此需要着重强调的是，活化能在氧化动力学方程的指数项，因此活化能的微小变化对整个反应的描述影响很大。因此，E和k1值的适当选择对于精确描述铝氧化过程是非常关键的。

实验工作表明，在氧化早期阶段（η＝0），反应速率不取决于氧化程度，该过程类似于单分子反应，此阶段氧化过程遵循线性定律，直到反应度达到0.1～0.3，此时铝表面快速氧化形成薄的无定形氧化层。在第二阶段中，氧化进程减慢并且遵循对数法则，由于前期生长形成了氧化层，氧化性物质必须渗透氧化层并迁移到铝／氧化铝界面才能继续氧化。(www.xing528.com)

基于不同氧化温度范围收集到的实验数据，文献中还讨论了其他模型。这些方法主要是估算氧化引起的释热，并与外部颗粒加热或热耗散进行对比。因此，点火可以用包括氧化反应焓的颗粒热传递模型来预测，文献综述显示了不同研究者报道的数据和使用模型之间存在很大差异。

1.4.2.4　基于相变过程的扩散

近期有关铝颗粒点火的研究提出，氧化过程是由氧和铝通过表面氧化物的非恒定扩散过程所控制的。重要的是，该过程假设加热过程扩散主要受多晶相变的影响。Trunov等［TRU 06］提出在低加热速率（＜40℃／min）下，在氧化物层发生了多晶态相变：无定形Al2O3→γ－Al2O3→δ－Al2O3→θ－Al2O3→α－Al2O3。

这些多晶态氧化铝的密度彼此不同，在表1.1中给出。

表1.1　不同氧化铝多晶态的密度

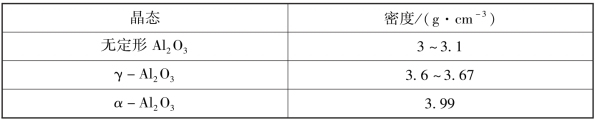
整个相变过程可以解释如下：在第一氧化步骤（形成薄的无定形氧化物）之后，天然无定形Al2O3层的厚度增加缓慢。在约550℃，氧化层超过约4 nm的临界值变成亚稳态。然后发生向γ－Al2O3的转变，这一相转化减小了氧化物层的厚度和扩散阻抗。在高加热速率下观察到薄氧化物层，相变还可能导致氧化物层的局部不连续性。所得的γ－Al2O3由于其晶体尺寸小而更为稳定。非晶态向γ－Al2O3的相转化可导致质量少量增加，这是因为氧化物层密度加大。连续γ－Al2O3层继续生长，部分转变为θ－Al2O3多晶，该过程发生在铝熔点（660℃）之后的第三阶段。最后，第四阶段对应于1 100℃以上的高温氧化，并形成了α－Al2O3。向热力学稳定的α－Al2O3转变过程可以是直接形成，或者通过许多中间相如δ－Al2O3和θ－Al2O3转化形成。不同铝氧化阶段的TGA曲线示例如图1.12所示。

上述Al2O3相变过程可以解释观察到的粉末逐步氧化，如通过TGA实验表征所示（参见图1.13），需要分析五个步骤来定量描述氧化过程：①非晶氧化物的生长；②非晶态到γ－Al2O3的相变；③γ－Al2O3的生长；④γ－Al2O3和α－Al2O3相变；⑤α－Al2O3的生长。图1.13给出了纳米铝粉在氩气和氧气环境中加热的TGA增重曲线，可以清楚地找到不同氧化物生长和相变对应区域，并给出了多晶态氧化物演变步骤。

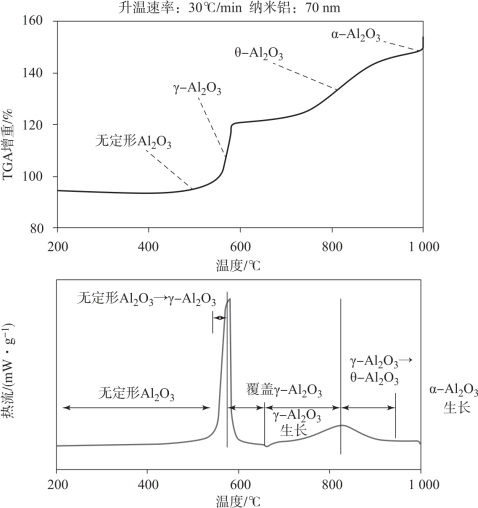
图1.12　不同铝氧化阶段的TGA曲线示例（根据文献［TRU 06］描述）

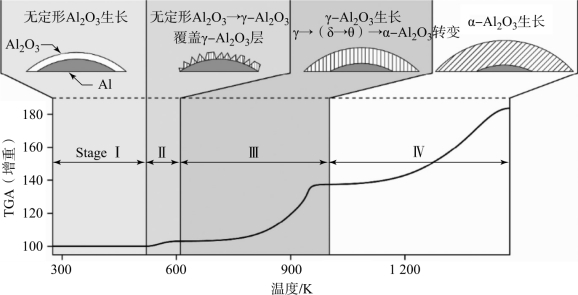
图1.13　氧化反应的不同阶段和分别生成的氧化铝相态的变化示意图［TRU 06］

该模型由Trunov等提出，用于预测不同尺寸的颗粒在不同温度下的点火情况，该模型很好地解释了大量先前文献报道的铝点火实验数据。