1.球面的近似展开
球面是典型的不可展曲面,只能作近似的展开。即假设球面由许多小块板料拼接而成,而每一块板料可看成是单向弯曲可展的,于是整个球面便可以近似地展开。
球面分割方式通常有分瓣法和分带法两种。球面分割数越多,拼接后越光滑,但相应的落料成形工艺越复杂。分割数的多少应根据球的直径大小和加工条件而定。
(1)球面的分瓣展开 球面分瓣展开法是沿经线方向分割球面为若干瓣,每瓣大小相同,展开后为柳叶形。球面分瓣展开的具体作法如下(见图2-87):
1)用已知尺寸画出球面的主视图和1/4断面图,并在主视图中画出极帽和分瓣。四等分圆弧15,等分点为1、2、3、4、5。由等分点向上引垂线,得球面一瓣(近似视为柱面)的素线。
2)用平行线法作出球面一瓣的展开图。
3)以O—1长为半径画圆,即为极帽的展开图。
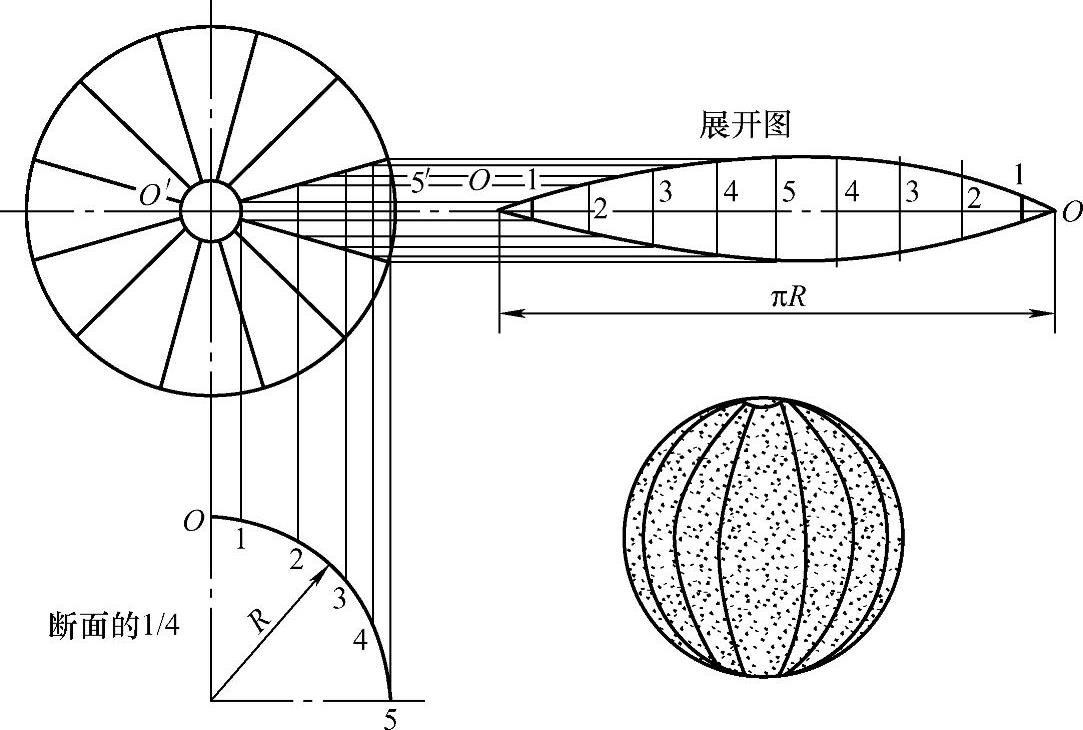
图2-87 球面的分瓣展开
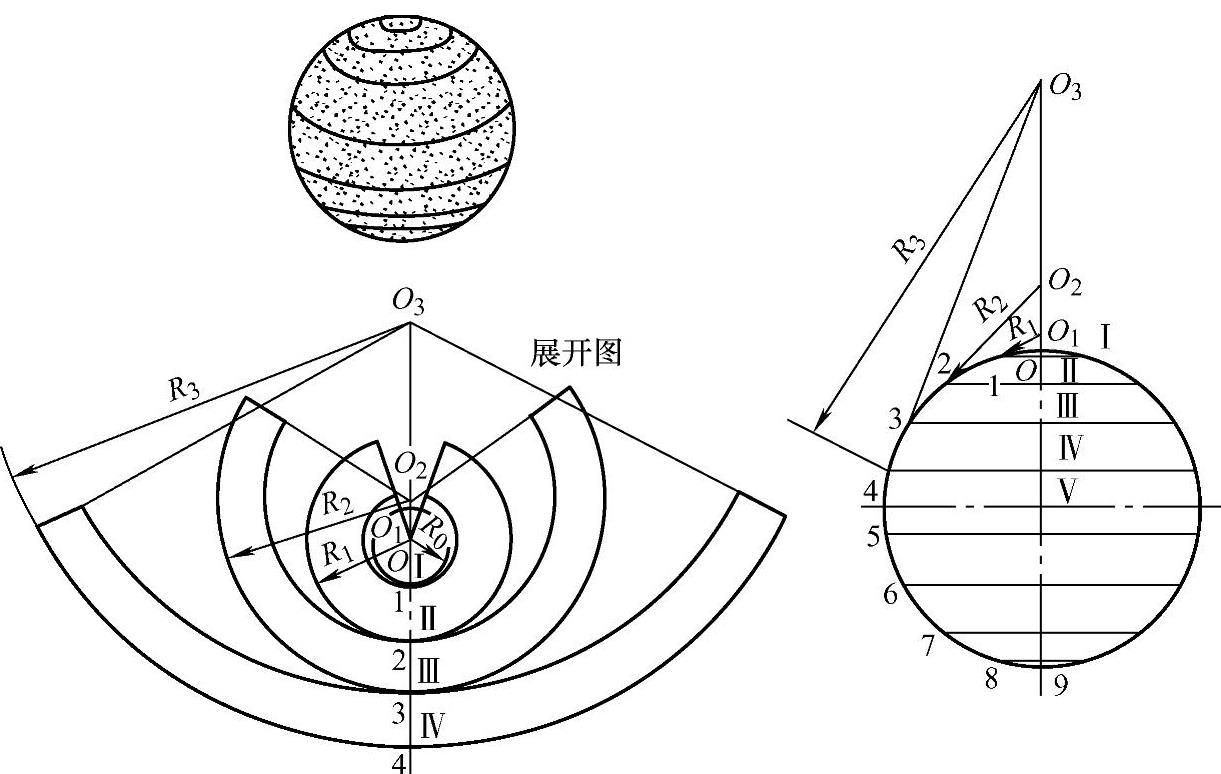
(2)球面的分带展开 球面分带法展开是沿纬线方向分割球面为若干横带圈,各带圈可近似视为圆柱面或锥面,然后分别作出展开,如图2-88所示。具体作法如下:
1)用已知尺寸画出球面的主视图,16等分球面圆周,并由等分点引水平线(纬线)分球面为两个极帽、七个带圈。
2)球面中间带视为圆筒,可用平行线法作出其展开图。
3)球面其余各带圈可视为正截头圆锥管,用放射线法展开,展开半径为R1、R2、R3。半径的求法:连接主视图圆周上1—2、2—3、3—4,并向上延长交竖直轴线于O1、O2、O3,得R1、R2、R3。
4)以主视图O—1为半径画圆,即为极帽的展开图。
(3)正螺旋叶片的近似展开 正螺旋叶片是圆柱形螺旋输送机的主要部件,它与螺纹一样有单、双线,左、右旋之分。单线螺旋螺距等于导程,双线螺旋螺距等于1/2导程。螺旋叶片通常按一个螺距或稍大于一个导程的螺旋面展开下料,弯曲成形后,再在机轴上拼接成连续的螺旋面。正螺旋叶片的近似展开方法很多,这里介绍应用较多的3种方法。
1)三角形法。三角形法是将螺旋面分成若干个三角形面,并将每一个三角形面近似地看作平面,求出实形。然后再将这些三角形的实形依次拼接在一起,即为螺旋面的展开图。具体作法如下(见图2-89):
①用正螺旋面的内、外直径d、D画出俯视图,12等分俯视图内、外圆周,等分点分别为0、2、4、…、12和1、3、5、…、13。以点画线和细实线交替连接各点。在主视图取h等于螺距,并12等分,由等分点引水平线,与俯视图内、外圆周等分点所引上垂线得对应交点,区别内、外圆各点,将各交点连成两条螺旋线,完成主视图。
②求实长,作展开。从主、俯视图不难看出,螺旋面上各三角形的细实线边为水平线,其水平投影反映实长,且各线实长相等;各点画线及内、外圆的等分弧为一般位置直线和曲线,投影不反映实长,可用直角三角形法求出。求出各线实长后,便可用其依次作出各三角形实长,完成展开图。
 (https://www.xing528.com)
(https://www.xing528.com)
图2-88 球面的分带展开
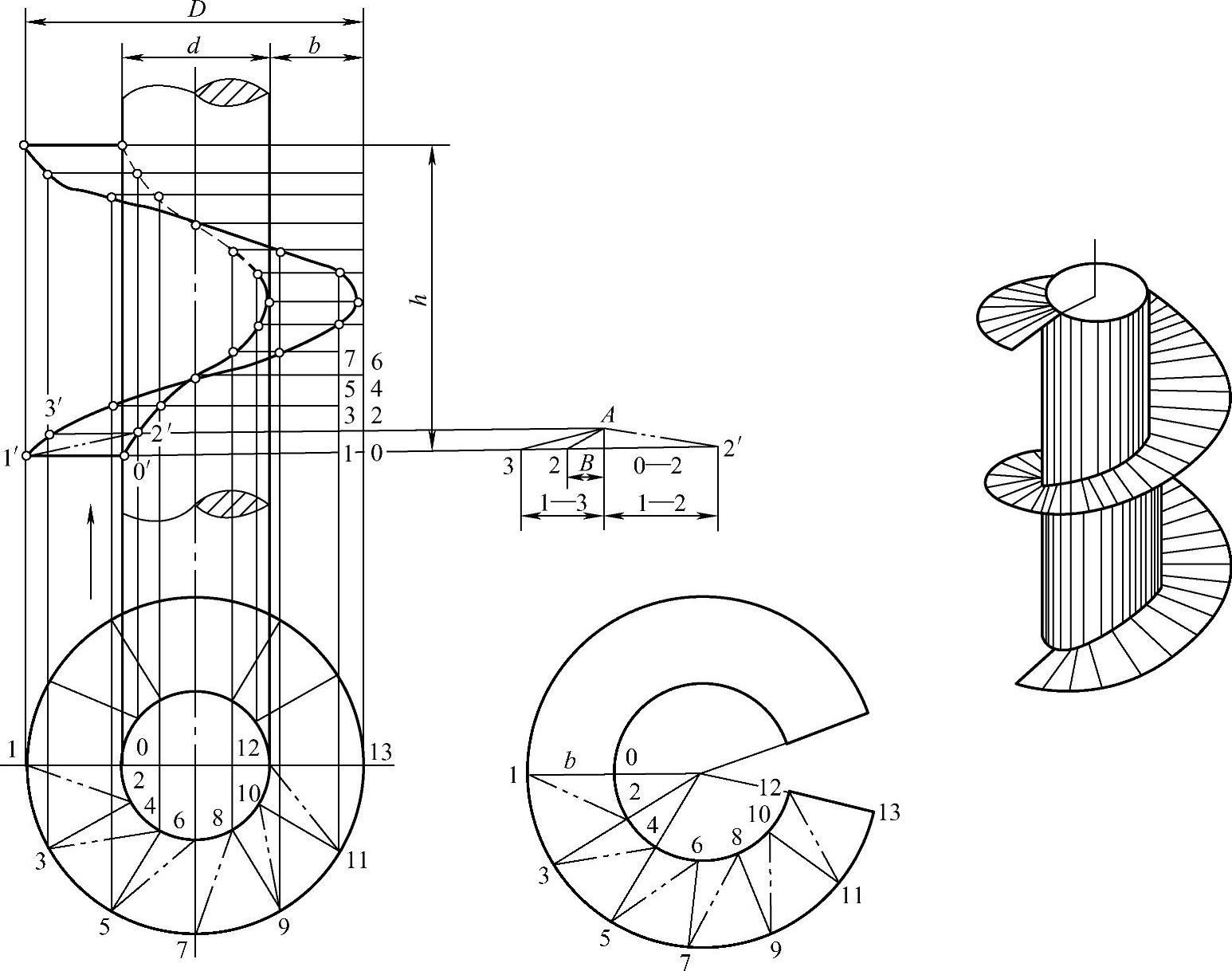
图2-89 正螺旋叶片的近似展开
2)简便展开法。由图2-89可知,一个螺距的正螺旋面,其展开图为一切口圆环。简便展开法是根据正螺旋面的外径D、内径d和螺距h,通过简单计算和作图,求出螺旋面展开图中切口圆环的内、外径和弧长,从而画出展开图。具体作法如下:
①用直角三角形法求出内、外螺旋线的实长l及L(见图2-90a)。
②作一直角梯形ABCE,使AB=L/2,EC=1/2,BC=1/2(D-d),且AB∥CE,BC⊥AB。连接AE、BC,并延长两线相交于O(见图2-90b)。
③取O点为圆心,OB、OC为半径画同心圆弧,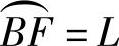 ,连接FO交内圆弧于G,即得螺旋面的展开图。
,连接FO交内圆弧于G,即得螺旋面的展开图。
3)计算法。
由图2-90可知:
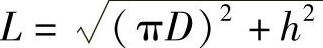
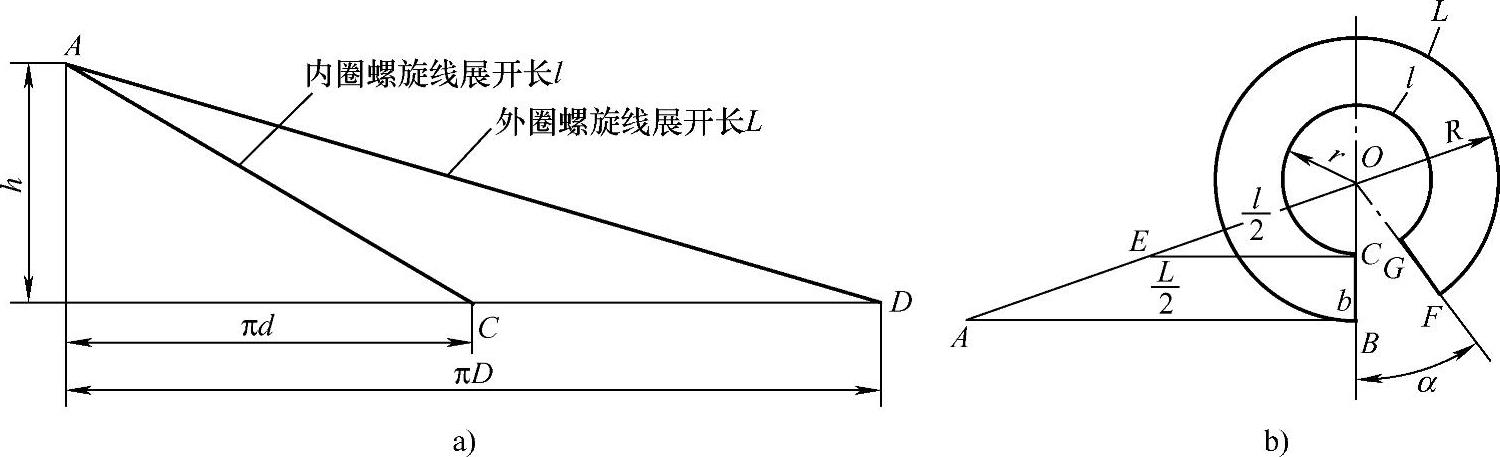
图2-90 正螺旋叶片的简便展开法
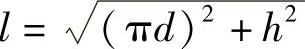
若展开图圆环的内、外径以r、R表示,则
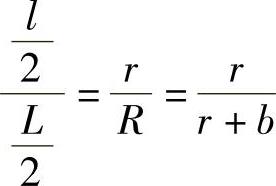
整理后得 l(b+r)=Lrlb=r(L-l)
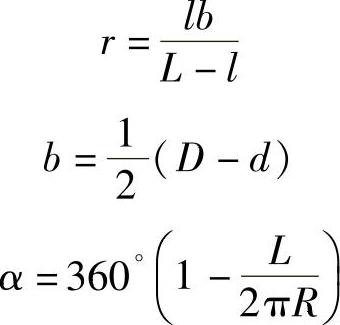
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




