数据采样插补法：用微小直线段逼近给定曲线

数据采样插补，又称为时间分割法插补，是用一系列首尾相连的按插补周期和进给速度进行分割的微小直线段来逼近给定曲线。假设微小直线段的长度为ΔL，进给速度为F，插补周期为T，那么ΔL=FT。可见，数字采样插补着重解决两个问题：一是如何选择插补周期，因为插补周期与插补精度、速度有关；二是如何计算在一个周期内各坐标值的增量值，因为有了前一个插补周期计算的动点位置值和本次插补周期内坐标轴的增量值，就很容易计算出本插补周期内的动点坐标值。

（一）数据采样插补法直线插补

对于刀具轨迹终点在第一象限内，坐标为E（Xe，Ye）的直线轮廓，如图2-4-8 所示，编程进给速度为F，插补周期为T，则每个插补周期的步长为

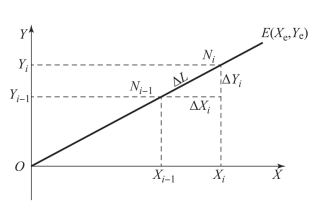
图2-4-8　数据采样插补法直线插补

方向X、Y 的位移增量分别为ΔX、ΔY，直线长度为

因为

令ΔL／L=K，那么

即

上述过程的软件流程图如图2-4-9 所示。其说明如下。

图2-4-9　数据采样插补法直线插补软件流程

①插补过程中使用的起点坐标、终点坐标及插补所得的动点坐标都是代数值，而且这些坐标值也不一定能转换成以脉冲当量为单位的整数值。但这些坐标均为带正负号的真实坐标。

②上述求取坐标增量值和动点坐标的算法并非唯一，如也可利用轮廓的切线与轴X 夹角的三角函数关系来求。(www.xing528.com)

③终点判别的方法有：由于插补点坐标和位置坐标增量均采用带符号的代数值进行运算，所以利用当前插补点（Xi，Yi）与该零件轮廓的终点（Xe，Ye）之间的距离Si来进行终点判别最简单，即判断条件为

当动点一旦到达轮廓曲线终点时，就设置相应标志，并取出下一段轮廓曲线进行处理。另外，如果在程序段中还要减速，则还需检查当前插补点是否已经到达减速区域，如果到达还需进行减速处理。

（二）数据采样插补法圆弧插补

圆弧插补的基本思想是采用直线逼近圆弧，计算较为复杂，并且有多种方法，下面仅介绍一种方法。

以第一象限顺圆弧为例，瞬时插补点P 的坐标为（Xi，Yi），Q为下一个插补点（Xi＋1，Yi＋1），那么假设进给速度为F，插补周期为T，=ΔL=FT，如图2-4-10 所示。与轴X 的夹角为γ，那么ΔXi=ΔLcos γ。因为γ =∠GPQ =∠GPM ＋∠MPQ，∠GPM =∠POE=αi，∠MPQ=∠POC=Δαi／2，所以γ=αi＋Δαi／2。

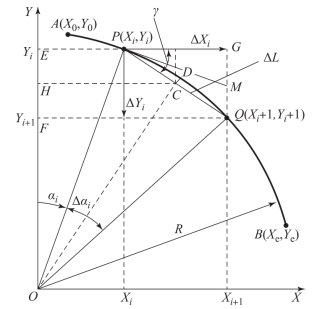
图2-4-10　数据采样法圆弧插补

因为是用直线段代替圆弧产生的误差δ，因此在△HOC 中，可得

一般合成进给量ΔL 相对圆弧半径足够小，δ 是ΔL 的高阶无穷小，可从上式中舍去。用上一步插补运算结果ΔYi＋1近似代替ΔYi，得

在开始第一步插补时，可取ΔY0为

式中，α0是圆弧起点A 与圆心的连线与轴Y 的夹角。

最后，可得ΔXi、ΔYi、Xi＋1、Yi＋1的计算式为

用这种算法算出的ΔXi和ΔYi与理论值虽有偏差，但可以保证每个瞬时点都位于圆弧上，只对进给速度有很小的影响，几乎不会影响加工轨迹精度。