实验样机结果与分析

为了验证控制策略的正确性，本节设计了一个小功率的实验样机。图8-92为级联型STATCOM的实验样机实物图，图8-93为其电气结构图。

在图8-93中，主回路包括一个220V/220V单相隔离变压器、单相0～220V调压器、无功负载（阻感负载）与STATCOM装置。实验样机主要参数见表8-5。

图8-92 5单元级联STATCOM实验样机实物图

表8-5 实验样机参数

每个单元悬浮电容电压的平衡是装置稳定运行的前提。因此在做样机实验时，首先需要验证单元悬浮电容电压平衡控制算法。装置在理想工况下，理论上分析不用加入单元悬浮电容电压平衡控制算法即可实现自平衡。因为实现了总电压控制以及电流控制，采用多载波移相调制时，每个单元母线电容在一个基波周期中充放电电流相同，故电压会实现自平衡。但在空载实验中，由于实际系统中的装置元器件参数的不一致性，以及控制误差（包括检测精度，多载波移相的相移误差），单元母线电压会出现偏差，如图8-94所示。

在图8-94中，总电压给定为200V，此时两个单元总电压为200V，说明电压外环稳定。但实际中U_dc1=110V，U_dc2=90V。可以得出控制算法不能将总的有功功率平均分配至2个单元中，此时需要加入平衡控制算法。在加入平衡算法后，实验波形如图8-95所示。

由图8-95可见加入了单元悬浮电容电压平衡算法后，U_dc1=U_dc2=100V，两单元的悬浮电容电压得到较好的控制。

在悬浮电容电压平衡控制实验完成以后，需要验证装置的带载能力。首先对2单元级联整流器工况进行带载实验，图8-96为2个单元直流侧分别带电阻整流负载实验的主回路电气连接图。

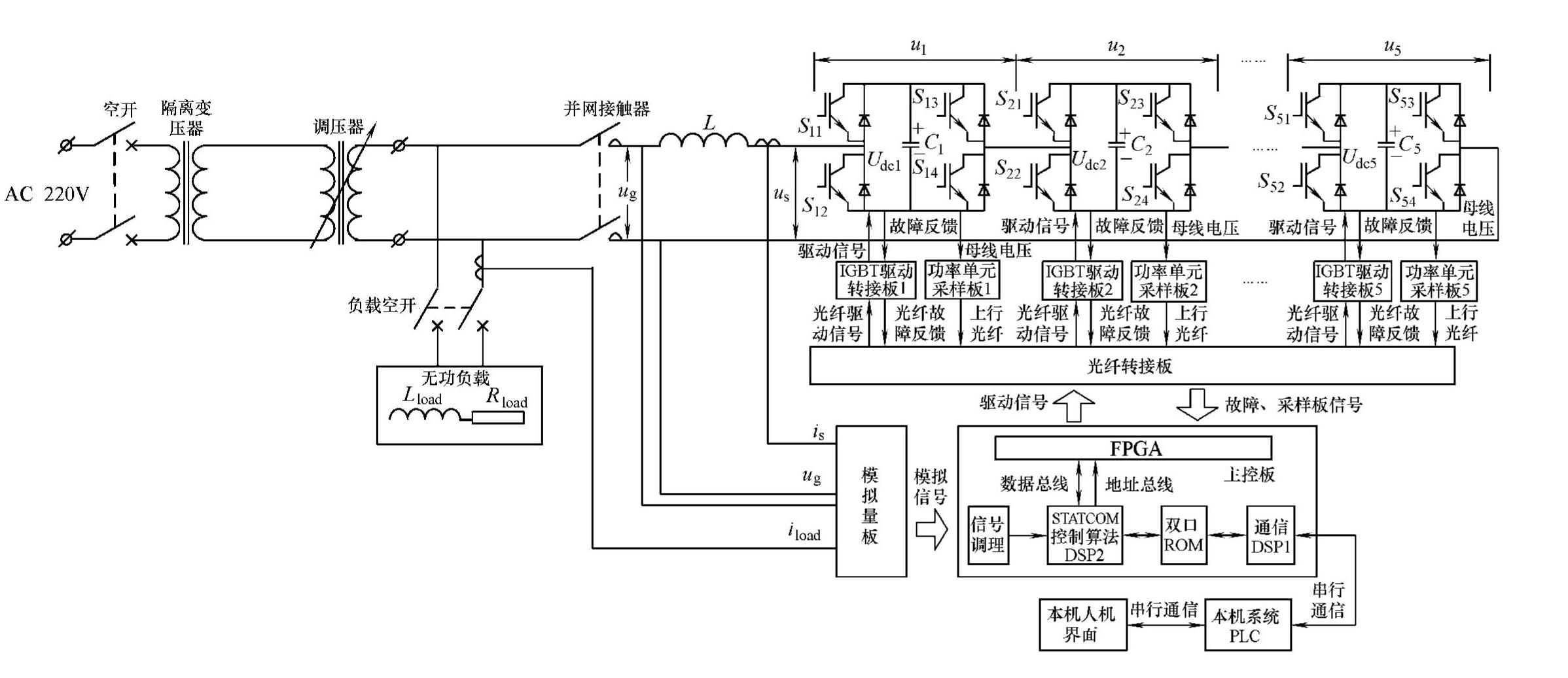
图8-93 5单元级联STATCOM实验样机电气结构图

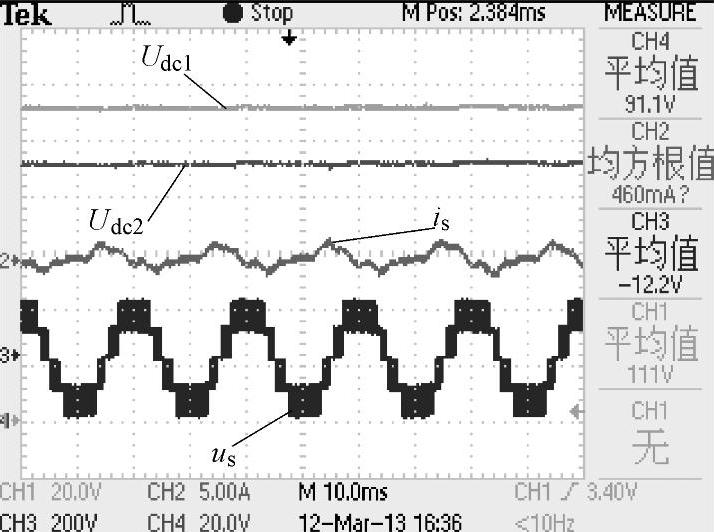
图8-94 两单元级联空载实验波形（未加入平衡算法）

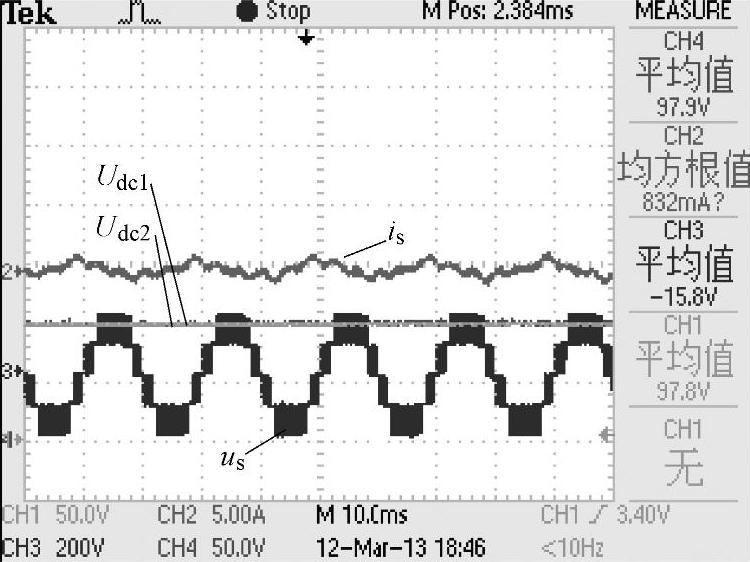
图8-95 两单元级联空载实验波形（加入平衡算法）

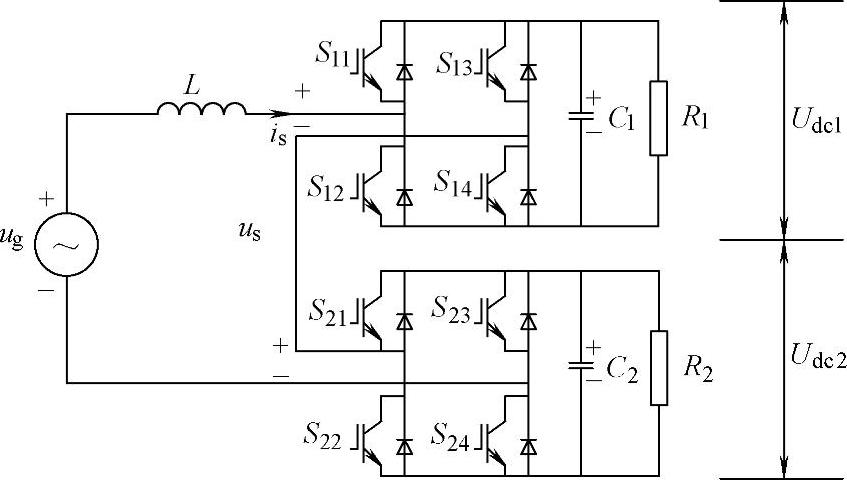
图8-96 两单元级联整流器工况主回路电气连接图

如图8-96所示，R₁=R₂=20Ω，为单元直流负载，C₁=C₂=3300μF，为单元直流侧悬浮电容。控制单元悬浮电容电压U_dc1=U_dc2=100V。图8-97为2单元级联整流器工况实验波形。

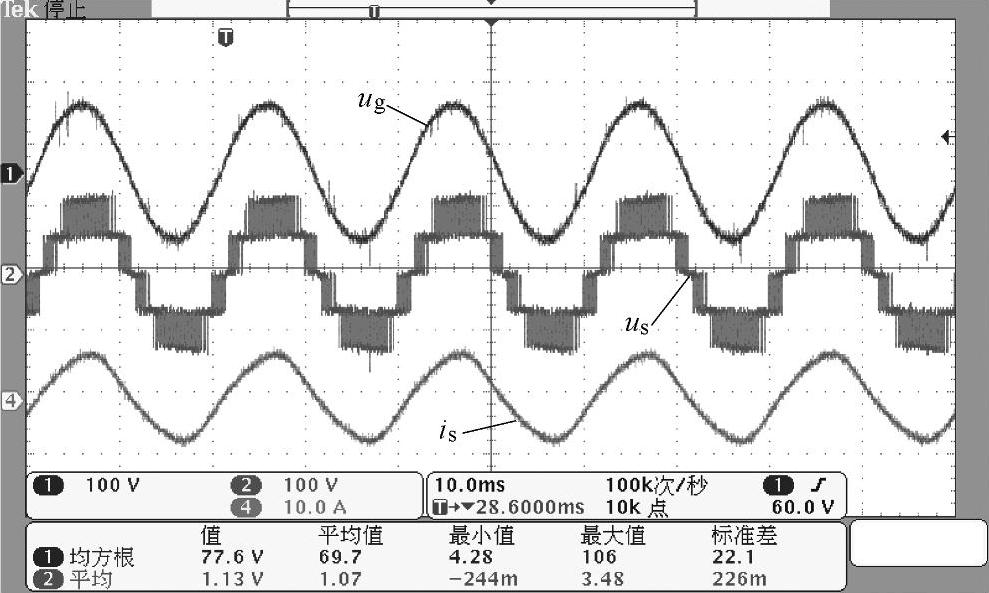
图8-97 2单元级联整流器工况实验波形

由图8-97可见i_s能够与u_g达到同频同相，此时装置以单位功率因数运行，运行于整流器工况。

图8-98为给定5A无功电流的无功发生工况实验波形。(www.xing528.com)

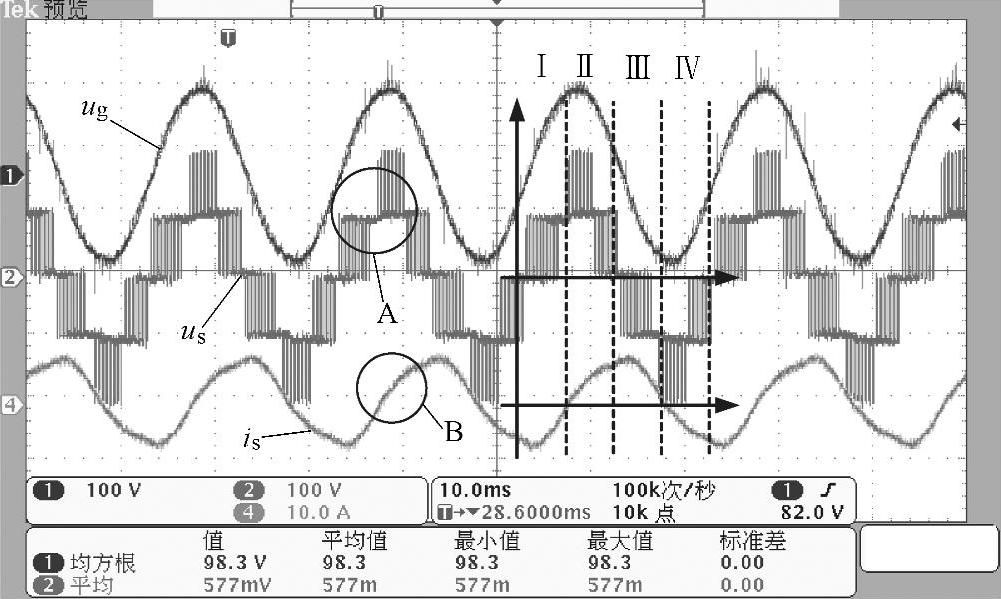
图8-98 2单元级联整流器工况实验波形

由图8-98可见i_s滞后于u_s约90°，为容性无功电流发生器工况。与整流器工况不同的是在u_s的峰值处，i_s存在一定的畸变。在图8-97和图8-98中，可以得出装置带载后两个单元的悬浮电容电压也能够较好的稳定于给定值。

在图8-98中可以看出i_s在B点出现的畸变是由于u_s在A点出现畸变。也就是说，A点电压出现畸变的原因就是导致B点电流畸变的原因。u_s出现了畸变，是由于调制波产生了畸变。由于2个单元的悬浮电容电压值都能够很好的稳定于给定值100V，所以可以断定总电压外环运行稳定。那么在控制算法层能够导致调制波出现畸变的只有内环电流准PR调节器和悬浮电容电压平衡控制策略。经观察，电流准PR调节器的误差输入较小，且无明显畸变，那么导致u_s在A点出现畸变就在于悬浮电容电压平衡控制策略。以单元1为例，在加入平衡算法后，调制波u₁与加入的调节量Δu₁在补偿容性无功时的仿真波形如图8-99所示。

在图8-99a中，调制波u₁在A点出现畸变。这是由于在从区域Ⅰ向区域Ⅱ切换时，由于调节方向改变，故调节量Δu₁有一个突变，如图8-99b中B点所示。如果采用自然采样法时，这种调节量的突变在单元之间是可以互相抵消的，不影响总电压输出。但是在实际系统中，都采用规则采样的方式来实现多载波移相调制。实验样机在实现方面采用非对称的规则采样，下溢和上溢中断相结合的方式。在FPGA中，每一个单元都有一个单独的载波调制模块，同时也是分别更新PWM比较器的。具体时序图如图8-100所示。

在图8-100中，可以看到2个载波移相模块更新PWM寄存器的时刻是不同的，模块2要滞后模块1T_d的时间。这种工作特性决定了每个单元的输出电压不能实时更新，也就导致了每个单元的调节量不能完全抵消，从而导致了图8-98中u_s在A点的电压畸变。由上文分析得出，每个单元加入的悬浮电容电压平衡控制调节量之和为零。如果不为零，那么会使装置输出的电压与闭环控制所计算出的电压出现偏差，导致系统的控制性能变差，甚至不稳定。但由图8-99b可见调节量的畸变幅值并不大，故而对控制系统的稳定性不会造成过大的影响。

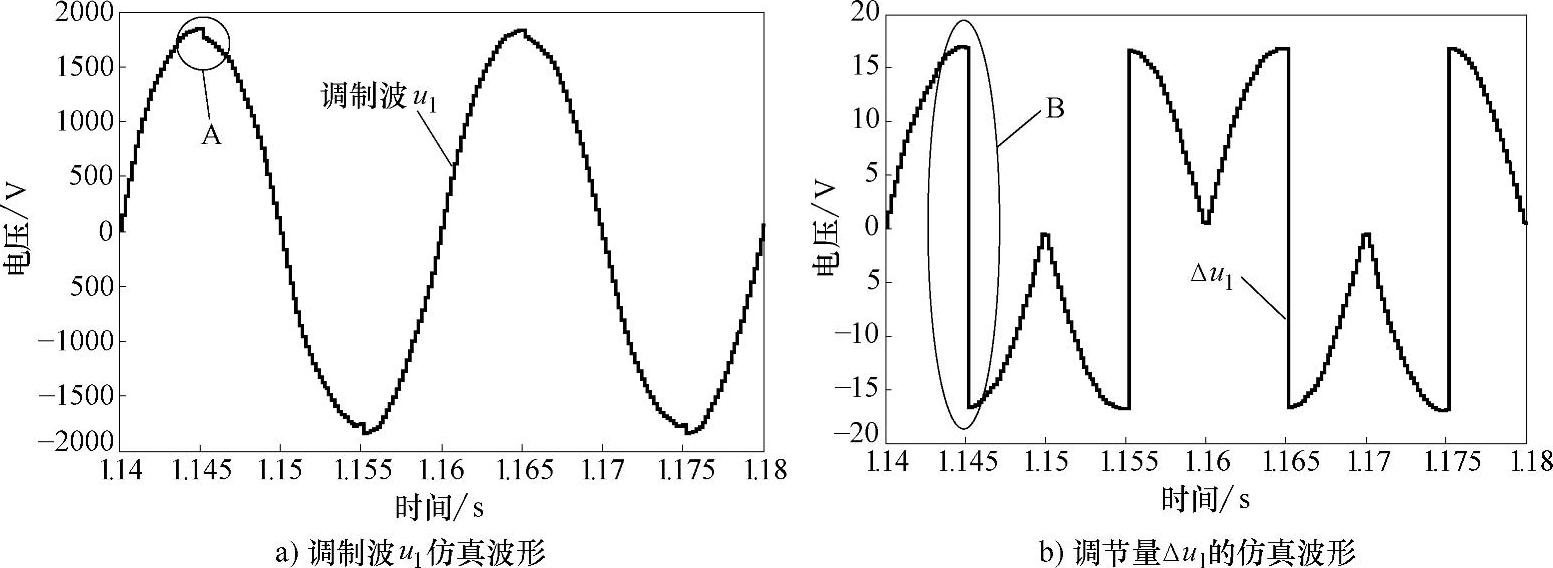
图8-99 单元1调制波u₁与加入的调节量Δu₁的仿真波形

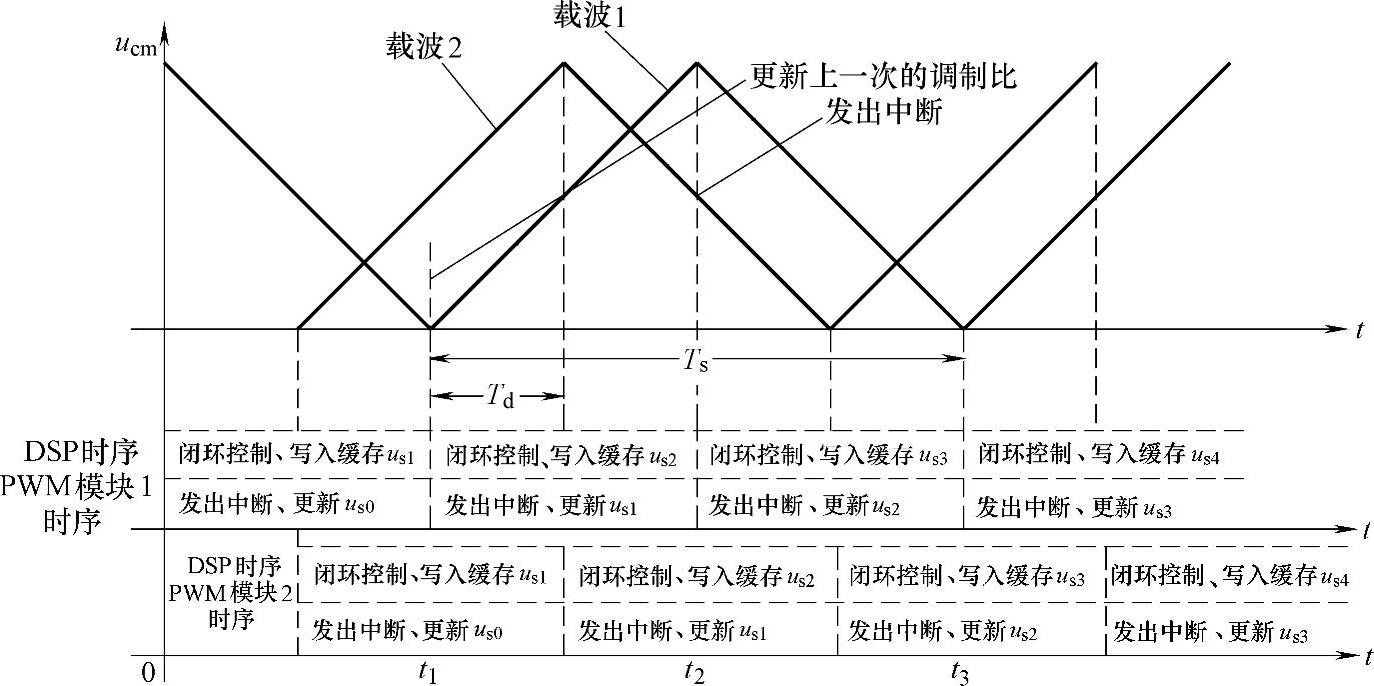
图8-100 2单元PWM模块时序图

图8-101为5单元级联的无功发生器实验，电气连接图如图8-93所示，实验条件由表8-6给出。由程序内部给定无功电流，实验中无功电流给定为10A。

图8-101a中，由于调制度较低，装置输出电压为9电平。同时，装置输出电流i_s在u_s峰值处也出现畸变。分析方法如上文所述。每个单元悬浮电容电压给定值为55V，能够得到较好的平衡控制。图8-102为单元1～单元4的悬浮电容电压波形。

采用50mH电感与15Ω电阻级联来模拟无功负载，电气连接图如图8-93中闭合负载空开。进行5单元级联的无功补偿实验，补偿前后的实验波形如图8-103所示。

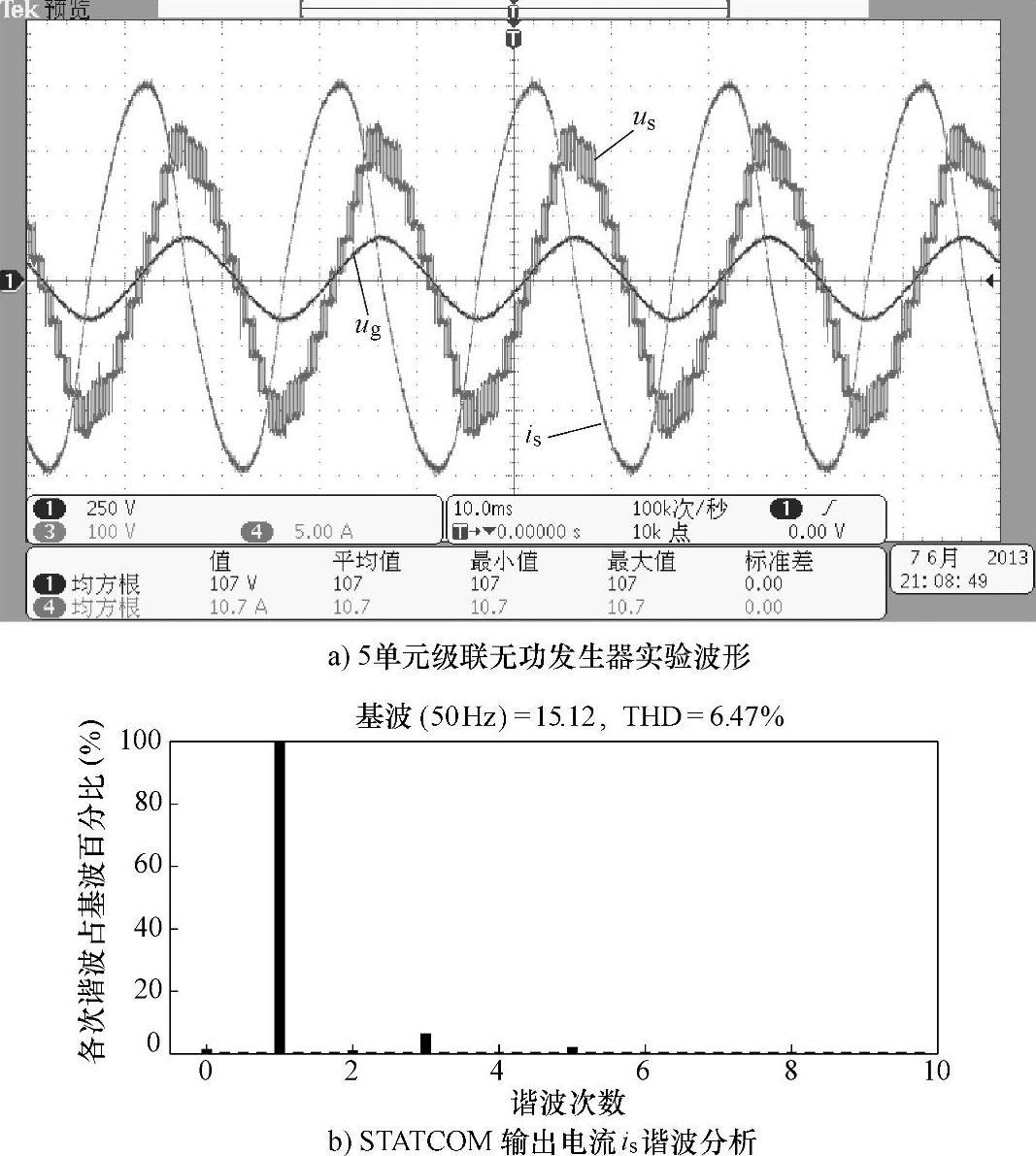
图8-101 5单元级联无功发生器实验波形

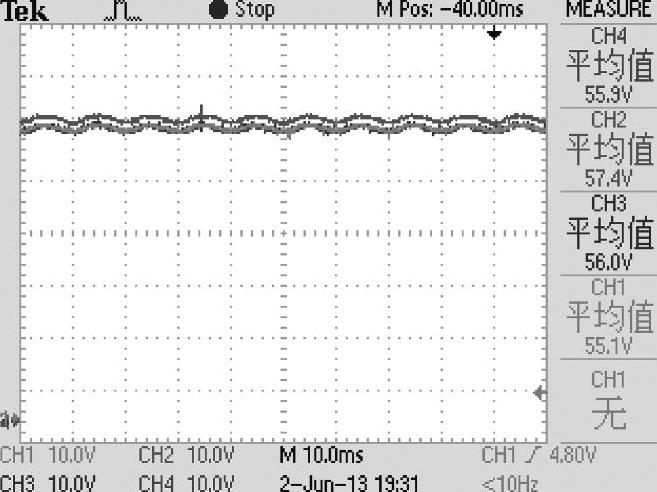
图8-102 单元1～单元4悬浮电容电压波形

在图8-103a中，可以看出i_g滞后于u_g一个角度，此时电网侧含有感性无功功率。在图8-103b中，i_g与u_g同频同相，此时电网侧达到单位功率因数。但由上文分析可知，在加入悬浮电容平衡控制算法后，i_s在A点存在一定的畸变，故导致ig在电流的峰值处B点存在一定的畸变。

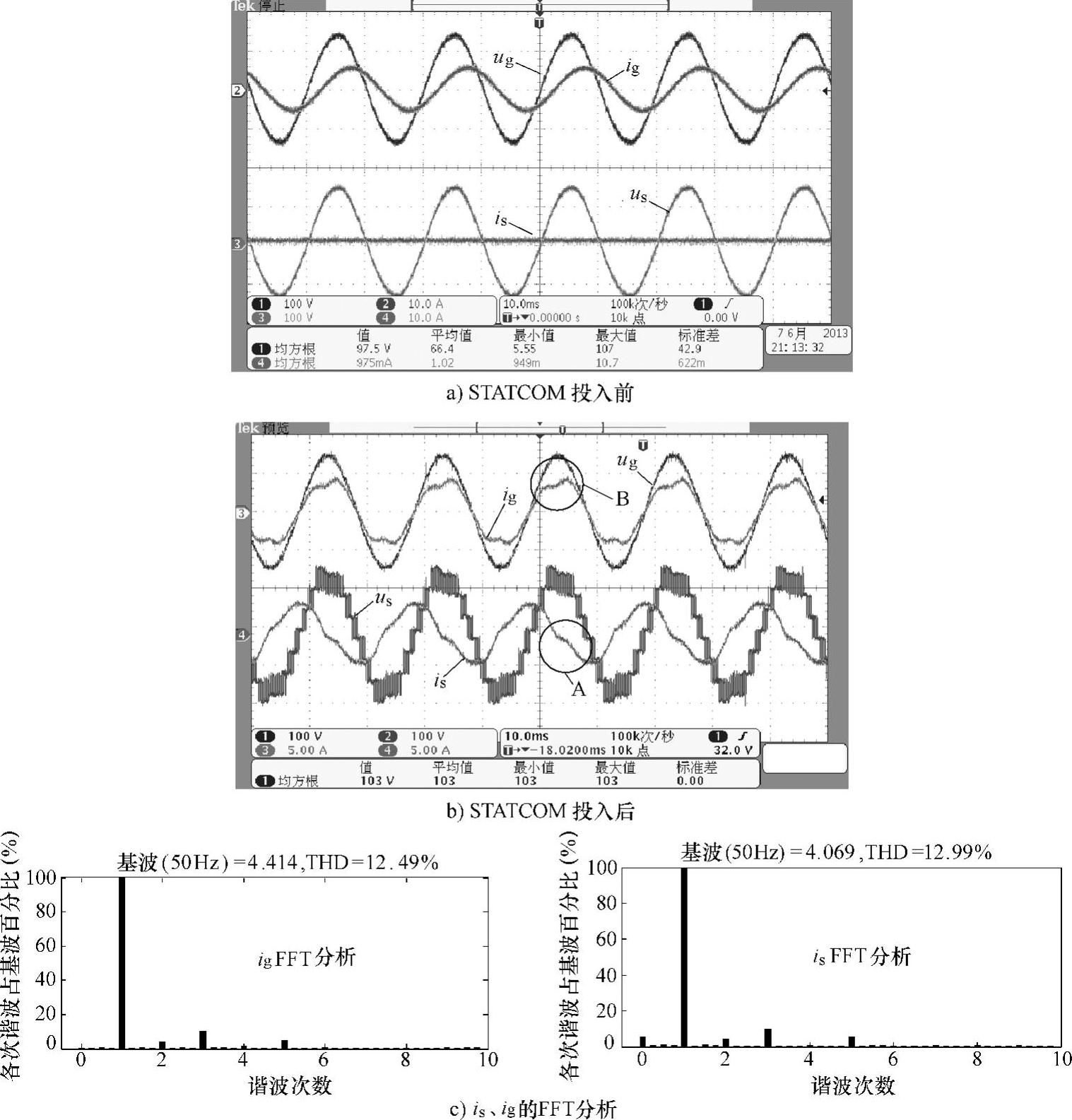
图8-103　STATCOM装置无功补偿实验波形

在对称的星接三相系统中，由于中点的存在，且各相对应单元的调制波相同，故由悬浮电容电压平衡控制算法所产生的电流产生的畸变可以互相抵消，但是在单相系统中，由于单元之间PWM更新时刻不同，会导致装置输出电流产生畸变。并且由于单相的功率波动，也会使输出电流产生一定量的低次谐波，如图8-103中的i_s。同时在控制系统设计时，往往满足一个条件，会对另外的某些控制量造成影响。从样机的实验结果来看，本章所提出的悬浮电容电压控制算法就是在牺牲一定的电流质量条件下，来达到控制各个单元的悬浮电容电压平衡。