MCC控制策略的优化方法

三相MMC是对称结构，因此，可以单个相单元作为研究对象，如图8-45所示为MMC一个相单元的等效电气图。

图8-45　MMC相单元等效电气图

在图8-45中，O点为MMC直流侧的假想中性点，N为电网电压参考点，u_si为电网i相相电压（i=a、b、c），i_si为i相相电流，u_i1为上桥臂电压，u_i2为下桥臂电压，u_dc与i_dc分别代表直流电压、直流电流，u_NO为交直流侧参考点之间的电压差。由基尔霍夫电压定律分析回路Ⅰ、回路Ⅱ，则MMC的微分方程组为

为了保持直流正负极电压的平衡，交流中性点或直流中性点必有一侧接地，系统对称运行时，u_NO=0。

将式（8-30）中的两分式分别相加、相减可得到MMC交、直流回路电压方程为

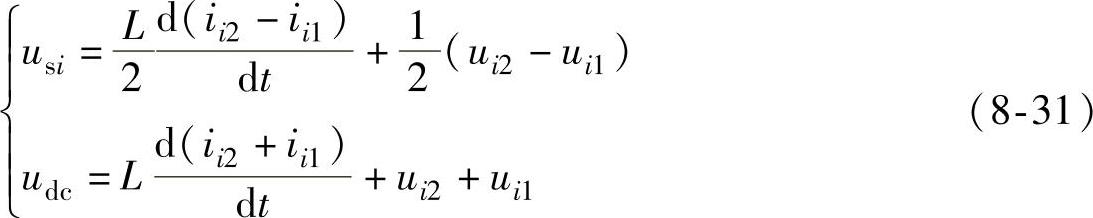
三相MMC的拓扑为对称结构，即有：每个相单元的上、下桥臂阻抗相等，交流侧相电流i_si流入MMC后，在上、下桥臂平均分配；三个相单元阻抗相等，直流侧电流流入MMC后在相单元之间平均分配。由基尔霍夫电流定律，可得MMC的电流关系为

在图8-44所示中，u′_a、u″_a为a′、a″相对于N点的电压。由电路结构可见，两点的电压分别等于电网电压减去电抗器上的压降，在直流回路电流脉动很小的情况下，两电抗器上的压降只与交流侧电流相关，而交流电流在上、下桥臂均分，并且方向相反，所以a′、a″两点为等电位电，研究MMC外特性时，将电抗器从MMC内部移到外部，a′、a″可被视为一点，该点电压u_i为MMC交流侧等效输出电压，此时MMC的外特性与传统电压源换流器一致。基于此，桥臂电压u_i1、u_i2可表示为

将式（8-33）中的两分式相减，可得MMC交流端的等效输出端电压表达式为

u_i=（u_i2-u_i1）/2 （8-34）

MMC-HVDC的控制策略包括对系统级控制和装置级控制。系统级控制主要作用是调节换流器的交流侧与直流侧传输的功率；装置级控制又包括MMC内部悬浮电容电压的控制、环流的抑制、产生开关器件的触发信号。

由图8-45所示与式（8-34）表明MMC的等效电路与两电平、三电平VSC有相同的外部特性，MMC系统级的控制可采用直接电流控制策略，其控制框图如图8-46所示。

图8-46　MMC-HVDC控制框图

在图8-46中，MMC-HVDC两侧环流站的控制系统结构对称，主要由电流内环控制器、外环电压控制器、锁相环和触发脉冲生产环节（调制）等几个模块构成。常见的外环控制器形式有定直流电压控制、定有功功率控制、定无功功率控制、定交流电压控制以及定频率控制等，外环控制器跟踪系统控制器给出的参考信号，为实现系统有功功率平衡，两端的换流站必须有一端采用定直流电压控制，另一端采用定频率控制或定有功功率控制；同时，根据换流站的具体控制目标，还可选择定交流电压控制或定无功功率控制。在向无源网络供电的直流输电系统中，一般送电端换流站采用定直流电压控制，受电端换流站采用定交流电压控制（因受端网络没有稳定供电的电源）。

图8-47所示为一端换流站直接电流控制的基本原理示意图。

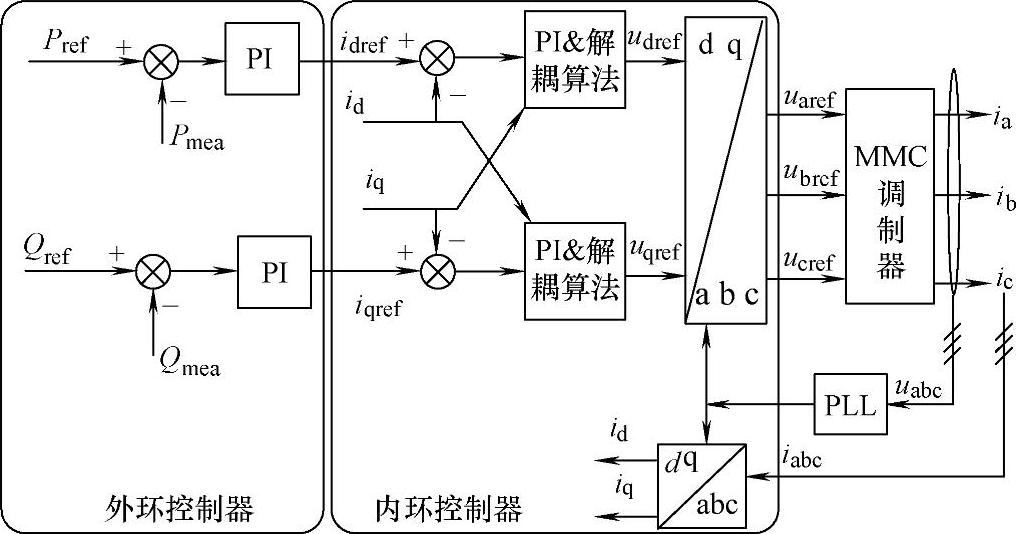
图8-47 换流站直接电流控制原理示意图

由图8-47可见，直接电流控制策略采用双环结构，即电流内环和功率（电压）外环，图中的P_ref，Q_ref分别代表需控制的有功类电量、无功类电量参考值。外环采用PI控制器，对换流器交直流侧传输的功率进行调节，给电流环提供指令信号i_dref和i_qref；电流环控制器可实现换流器交流侧有功电流和无功电流的解耦独立控制，其中电流前馈解耦控制算法为

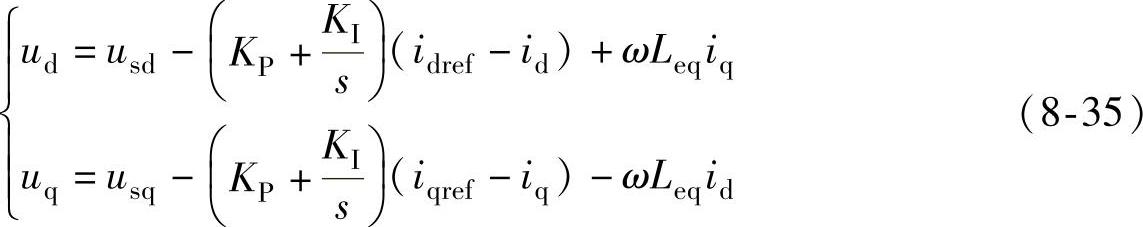
由于直接电流控制策略中的各矢量以电网电压矢量为定向基准，因此首先要准确获取电压矢量的相位信息，否则各矢量无法精确定向，控制目标无法达到。为实现精确锁相，需对锁相进行改进。参考文献[203]提出了基于双同步旋转坐标系的锁相环（Double Synchronous Reference Frame PLL，DSRF-PLL），双同步坐标系与静止坐标系的空间位置如图8-48所示。

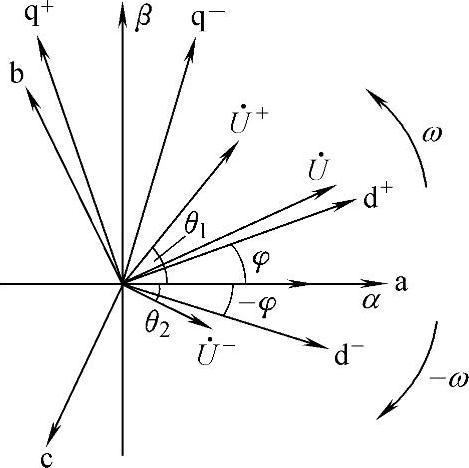
图8-48 双同步旋转坐标系空间位置

在正序旋转坐标系中，正序分量为直流量，负序分量为2倍频交流量，其幅值等于负序旋转坐标系中电压的直流分量；在负序旋转坐标系中，负序分量为直流量，正序分量为2倍频交流量，其幅值等于负序旋转坐标系中电压的直流分量。2倍频分量使得两式相互耦合，可通过低通滤波器得到正负序分量的近似值。正序坐标系下的信号经滤波后得到正序分量的近似值，负序坐标系下的信号经滤波后得到负序分量的近似值，将这些近似电压作为前馈量可消除正、负序旋转坐标系中的两倍频分量，得到正负序分量的检测值。图8-49所示为基于双同步旋转坐标变换的锁相环与正负序检测算法框图^[204]。

图8-49 锁相环与电压正负序分量检测

在图8-49中，锁相环和电压正序、负序分量的检测组成闭环结构，正序电压q⁺轴分量经滤波后的信号为锁相环节输入，锁相环精确锁定基波电压正序分量的相位，利用该相位得到双同步旋转坐标下的电压表达式，通过解耦单元消除表达式中正负序分量的相互影响，完成正负序分量的检测。

当电网发生不对称故障时，电压、电流包含了正序、负序分量。根据瞬时对称分量理论，三相三线系统的不对称电量可以表示为正序分量与负序分量之和，双同步旋转坐标系下MMC的数学模型为

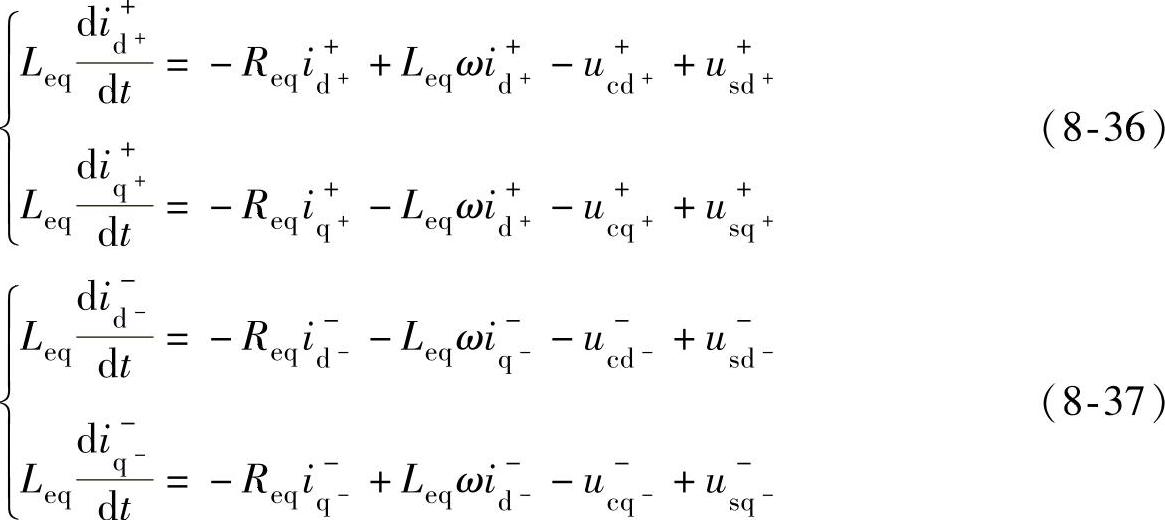
上述数学模型中，L_eq=L/2，R_eq=R/2，L、R分别为桥臂电抗器的电感值与电阻值。

为抑制负序电流，增加负序电流解耦控制回路，与正序电流控制器共同完成双序电流控制，负序电流指令值设为0，通过负反馈控制抑制负序电流，电网不平衡时整个控制系统框图如图8-50所示。(www.xing528.com)

MMC的电容稳压控制是MMC装置级控制的关键，诸多学者、研究人员对此做了深入研究与实践，目前，主要有两大思路：①稳压控制策略叠加到PWM调制中，首先构造子模块电压的负反馈控制器，电压期望值与测量值做差，经PI控制器得到稳压指令，该指令值与其他指令值共同构成MMC子模块的调制电压；②调制部分与稳压控制分为两部分，调制策略可以采用PWM方式、SVPWM方式或NLM方式，调制部分决定每个桥臂投入子模块的数目，稳压控制部分根据电容电压反馈值、桥臂电流的方向决定具体投入哪些子模块，这种控制策略中包含了电容电压排序，在此将其称为基于排序的电压平衡控制策略。下面分别介绍上述两种控制策略。

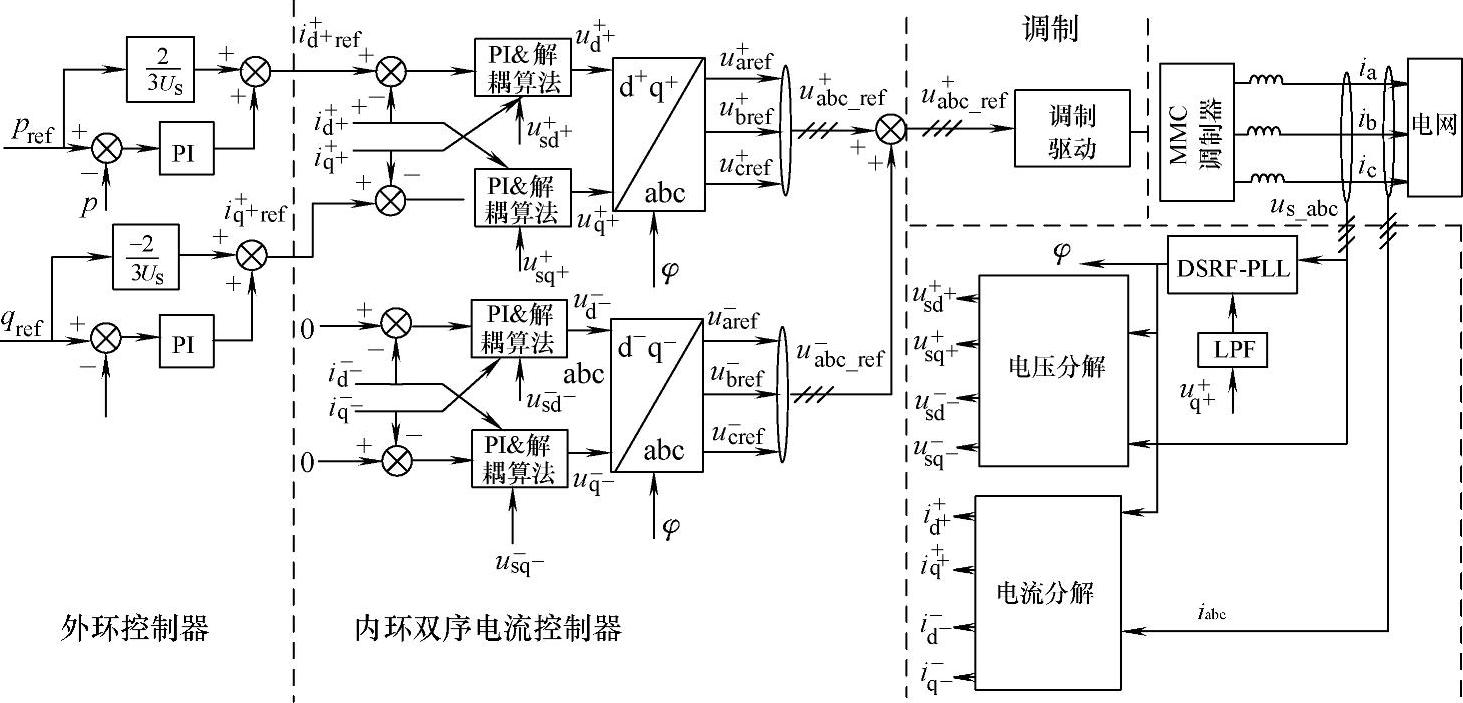
图8-50 电网电压不平衡时的MMC-HVDC控制框图

1.叠加到PWM调制中的电容电压控制策略

现以图8-43a所示的三相MMC为例分析，每个相单元有8个子模块，换流器每一相的工作原理相同且相互独立。为避免公式重复，仅选择某一相分析。根据前面推导的MMC数学模型即式（8-31），可得直流侧电压方程为

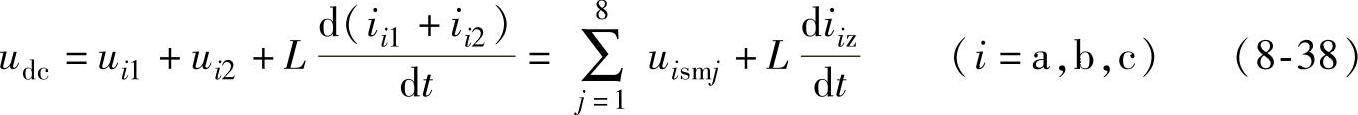
式（8-38）与MMC交流侧负载无关，为避免混淆将此KVL（基尔霍夫电压定律）回路称为“直流回路”，并定义i_iZ=i_i1+i_i2为MMC在i相直流回路中的电流，其包括了1/3的直流母线电流与流过i相的相间环流，参考方向采用从直流母线正极P经MMC相单元流向负极N的方向。

电容电压的控制可分为两部分设计：稳压和均压控制，即保持母线电压的稳定，同时电压要在各子模块电容间平均分配，图8-51所示为叠加到PWM调制中的电容电压控制策略示意图。

在如图8-50a所示的稳压控制算法中，基于负反馈的电压控制器使子模块电压的平均值ū_ci跟踪指令值u^∗_c。令直流回路电流的指令值为电压控制器的输出值i^∗_iZ，即

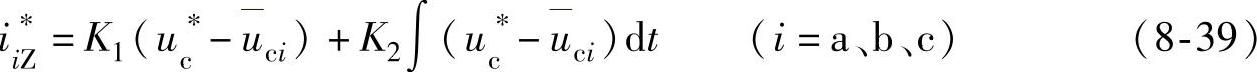
稳压指令值i^∗_AA为电流控制器的输出，即

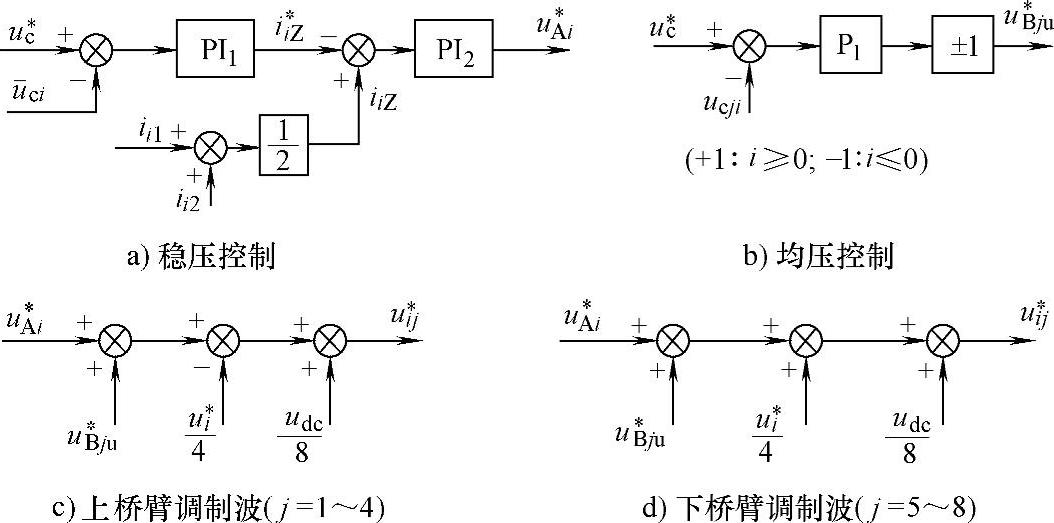
图8-51 叠加到PWM调制中的电容电压控制策略示意图

当子模块电容的实际电压平均值小于指令值时，电压控制器输出增加，即直流回路电流指令值增加（电流为正时，给开通的子模块充电）。根据式（8-40），若要保证直流回路电流增加，需要减小子模块的输出电压之和，式（8-40）描述的控制器可得到一个减小的电压指令（若控制器符号反向选择，无法实现控制目的）。在此调节过程中，对直流回路电流进行反馈控制，在不影响负载电流的情况下实现了对子模块平均电压的控制。

如图8-51b所示的均压控制算法，根据桥臂电流的方向确定均压指令的值的极性，同时因为电压的调节是一个快速动态调节过程，可采用比例调节器。其工作原理为：当某个子模块的电压值高于指令值时，需要给该子模块放电（或减小充电时间），桥臂电流大于0时，控制器输出一负的指令，减小其充电时间；当桥臂电流小于0时，控制器输出一正的指令，增加电容的放电时间。当某个子模块的电压值小于指令值时其工作原理，读者可自行分析。

图8-51c所示为上桥臂子模块的调制波产生方法。根据式（8-33）u_i1=-u_i+u_dc/2，在MMC交流输出电压期望值u^∗_i已知的条件下，上桥臂电压期望值为u^∗_i1=u_dc/2-u^∗_i，桥臂电压期望值平均分配到每个子模块再与桥臂的稳压、均压指令叠加得到上桥臂的调制电压为u^∗_ij=u^∗_i1/4+u^∗_Ai+u^∗_Bju=u_dc/8-u^∗_i/4+u^∗_Ai+u^∗_Bju，（j=1～4）。图8-51d所示为下桥臂子模块的调制波产生方法，其原理与图8-50c所示相同。

2.基于排序的电压平衡控制策略

如前所述，调制环节确定桥臂应开通的子模块的数目，均压控制算法确定具体开通哪些子模块。调制算法可选择基于载波移相的正弦脉宽调制策略（SP-WM）^[205]，也可选择最近电平逼近调制法^[206]（NearestLevelModulation，NLM），后一种方法属于低频调制，开关损耗低，在高压直流输电领域更具优势。本节对两种方法都加以介绍，后面章节研究MMC-HVDC控制策略时采用低开关频率的NLM调制方法。

图8-52所示为基于载波移相的SPWM调制与电容均压控制框图。电压控制环与上一小节所提的稳压控制原理相同，u^∗_i为换流站控制器下发的指令，它根据期望的交流电流（控制换流器与交流网络间传输的有功与无功）得到。调制环节是基于PWM调制原理发展而来，不同之处在于当调制信号与载波相交时决定哪个开关器件动作，这样，在换流器的交流侧输出电压实现多电平化的同时，可实现电容电压的平衡控制。对于8单元MMC换流器的每个相单元需要8路三角载波，载波之间互差360°/8，一个桥臂使用4路载波，分配给同一桥臂的载波互差360°/4。与载波比较的调制信号有两路，分属上下桥臂，表达式为

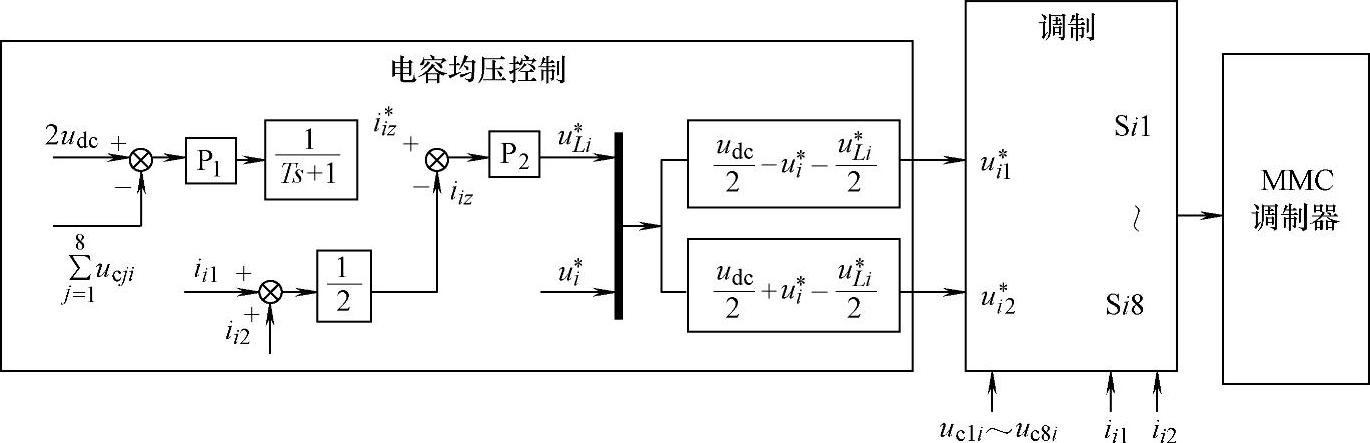
图8-52 基于载波移相的SPWM调制与电容均压控制框图

该控制策略的原理为：调制波与载波相交时，对应桥臂的一个子模块需要改变状态，当调制波大于载波时，处于旁路状态的一个子模块转变为投入状态，当调制波小于载波时，处于投入状态的一个子模块转变为旁路状态。该算法首先按电容电压从高到低的顺序对子模块进行排序，当子模块状态需要改变时，根据桥臂电流的方向决定选择电压最高或最低的子模块，子模块的选择方法控制程序流程如图8-53所示。

参考文献[203]介绍了最近电平逼近的调制方法，实现方便简单，换流器能提供的电平数目越多，性能越好。图8-54所示为最近电压逼近法原理示意图，最近电平逼近的基本思路：计算最接近调制波的阶梯波的电平数，根据换流器的开关状态与输出电压的关系确定开关器件的状态。

图8-53 基于载波移相的SPWM调制与电容均压控制原理框图的子模块的选择方法控制程序流程

对于MMC，桥臂电压期望值除以子模块的电容电压，取整得到需投入的子模块的数目。考虑相单元投入的子模块数为N/2，是常数，结合式（8-33）可得

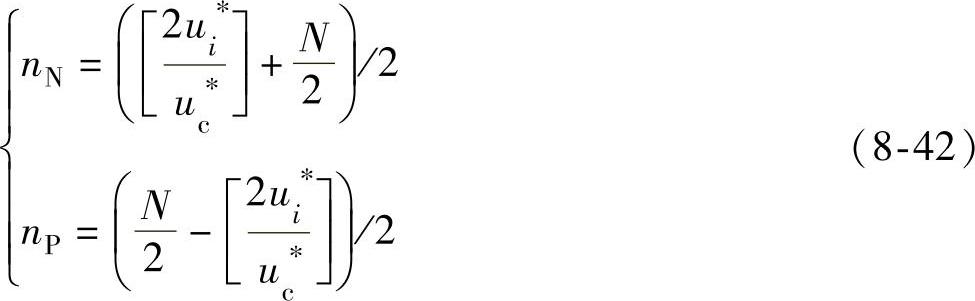
式中，n_N为下桥臂需要开通的子模块数目，n_P为上桥臂需要开通的子模块数目，N为相单元子模块的总数，u^∗_i为MMC交流输出相电压期望值，u^∗_c为子模块电压期望值。桥臂电流的极性与各子模块电容电压的测量值决定具体开通哪个子模块，即：当电流为正时，先投入电压低的模块；当电流为负时，先投入电压高的子模块，按此原则实现同一桥臂内电容电压的均衡控制，其原理如图8-55所示。

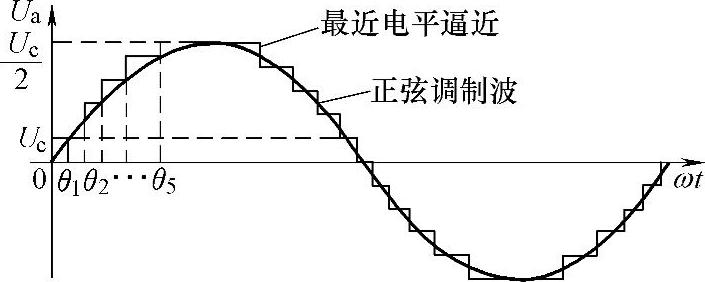
图8-54 最近电平逼近法原理示意图

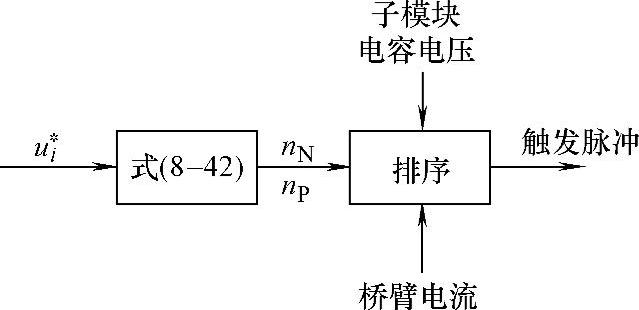
图8-55 基于NLM的电容均压控制