电流环的PIR调节器采用方法

对于带单相H桥负载的三相PWM整流器，由于负载输出功率包含2ω_o角频率的脉动分量，要维持直流母线电压恒定，PWM整流器d轴有功电流给定值必须包含2ω_o角频率的脉动分量。但是若电流内环采用PI调节器，不能实现对2ω_o角频率分量的无静差跟踪控制^[172]。这是因为PI调节器是线性调节器，对直流分量增益为无穷大，但对交流分量增益为有限值。为了解决这一问题，下面主要针对电流环的无静差跟踪控制^[173]和扰动抑制问题进行研究。

由前面对双环控制策略分析可知，电流内环的控制框图如图5-42所示。图中，G_i（s）为电流调节器的传递函数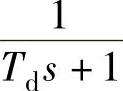；为电流环采样延迟和PWM控制的小惯性特性；r为扰动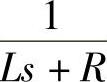，为主回路传递函数。根据图5-42所示的电流内环控制框图，可得从电流给定到电流误差的闭环传递函数为

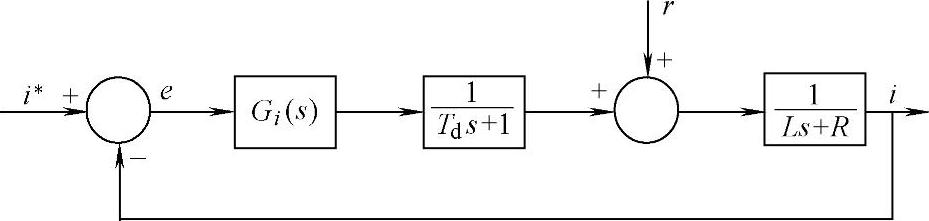
图5-42 双环控制系统的电流内环控制框图

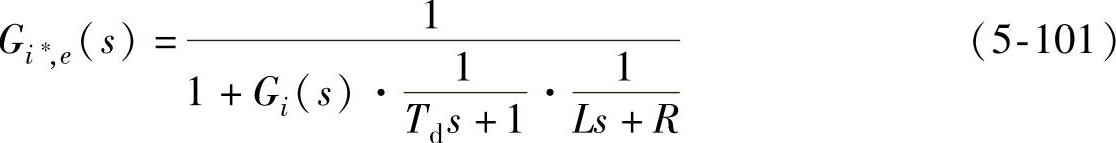
从扰动到电流误差的闭环传递函数为

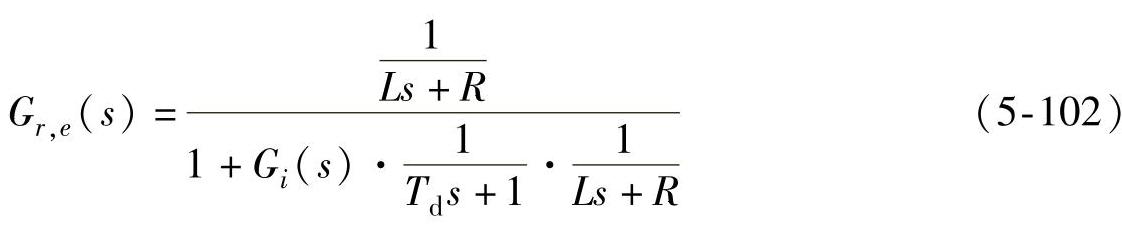
1.电流环PI调节器

当电流环控制器为PI调节器时，令其传递函数为

将式（5-103）代入式（5-101）中可得

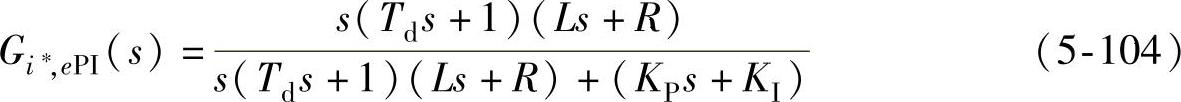
将式（5-103）代入式（5-102）中可得

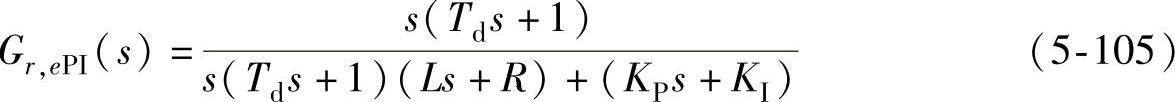
假设电流内环PI调节器的参数选取适当，使闭环内环稳定，即式（5-104）和式（5-105）所描述的闭环传递函数极点均位于复平面的左半平面（不包括虚轴）。

当三相PWM整流器带直流负载或三相逆变器平衡负载，且PWM整流器处于稳态时，d轴和q轴电流的给定值与实际值均为常量，此时相应的交叉耦合项ωLi_d和ωLi_q也为常量，则由交叉耦合项造成的扰动也为常量。为此可得，电流给定值和交叉耦合造成扰动的数学模型均为阶跃函数，可分别假设为

式中，K₁₁、K₁₂均为常数，则电流误差e对这两个输入量的响应分别为

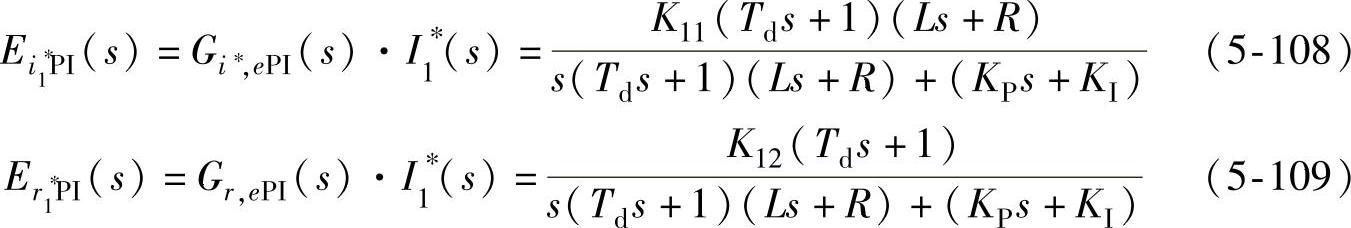
式（5-108）和式（5-109）均满足拉氏变换终值定理条件，因此由拉氏变换终值定理得到系统的稳态误差为

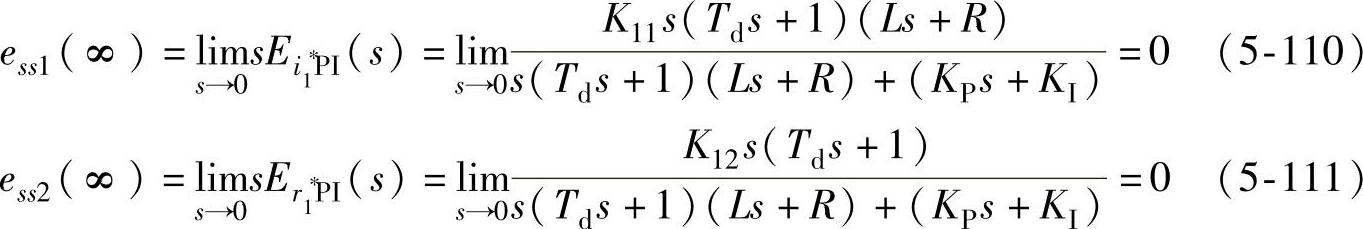
由上述理论分析与推导可知，电流误差对电流给定值和扰动的阶跃响应稳态误差均为零，这也是三相PWM整流器带直流负载或三相逆变器带平衡负载时具有很好的稳态性能的原因。另外，从扰动角度考察可发现，当电流内环不采用前馈解耦时，虽然电流环的动态性能会受到影响，但由扰动造成的电流误差为零，因此不会影响其稳态性能。

当三相PWM整流器带单相H桥负载时，由前面分析可知，d轴电流给定值由直流分量和2ω_o交流分量组成。其中直流分量产生的影响前面已有详细的分析，这里只着重对2ω_o交流分量产生的影响作分析。

电流给定值和交叉耦合引起的扰动都包含2ω_o交流分量，其数学模型可设为

式中，K₂₁、K₂₂均为常数，则电流误差e对这两个输入量的响应分别为

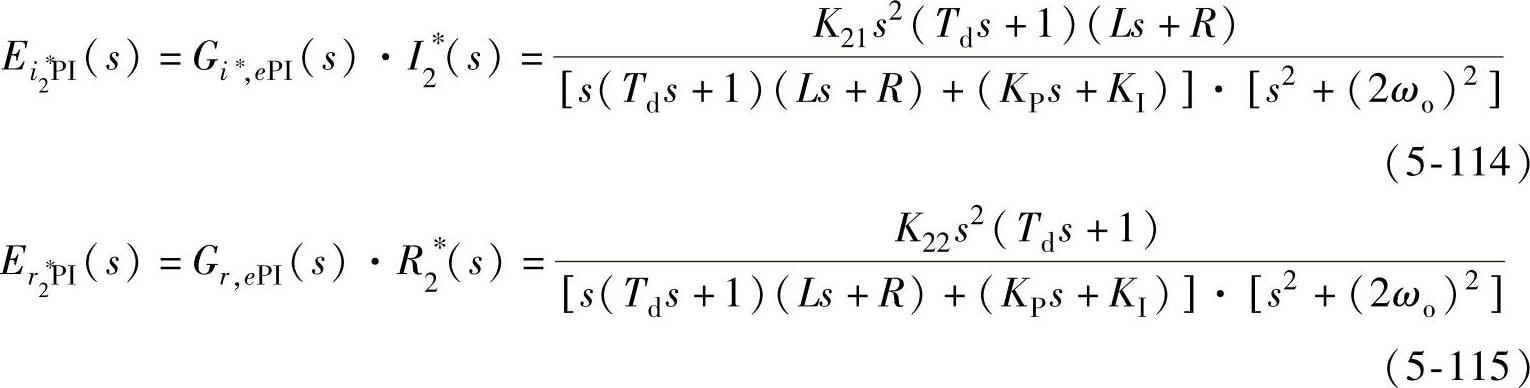
由于式（5-114）和式（5-115）均含有一对共轭极点±j2ω_o，不满足拉氏变换终值定理条件，所以利用终值定理得不到系统稳态误差为零的结论，这也进一步表明电流内环采用PI调节器时不能对2ω_o交流分量实现无静差跟踪控制，也不能消除交叉耦合扰动中2ω_o交流分量的影响。

2.电流环PIR调节器

由上述分析可知，2ω_o角频率的交流分量作为有功电流给定值或扰动输入时，电流误差响应的拉普拉斯变换会包含±j2ω_o这对共轭极点，从而响应中也会出现2ω_o角频率的波动。

对比输入为直流量和2ω_o角频率交流量的响应，可发现直流量的阶跃响应引入了一个极点s=0，但系统的闭环传递函数中含有s=0的零点，零极点正好对消，使电流误差响应信号的极点都位于复平面的左半平面，能实现阶跃响应的无静差跟踪控制。借鉴该思路，当2ω_o角频率的交流量作为输入信号时，要实现无静差跟踪控制，则需要电流误差的闭环传递函数包含零点s=±j2ω_o^[174]，该零点可由电流调节器的极点引入。因此可将电流调节器的传递函数定义为

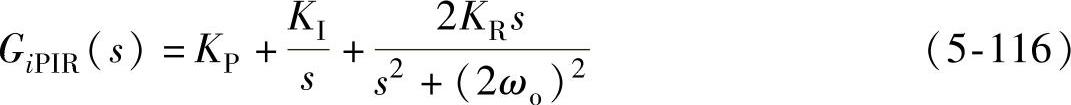
在参考文献[175]中将式（5-116）表示的调节器称为比例积分谐振调节器（Proportional Integral Resonant，PIR）。(www.xing528.com)

设谐振点频率为2f_o=90Hz，其谐振调节器的传递函数为

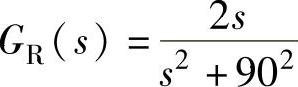
图5-43所示为其幅频特性。

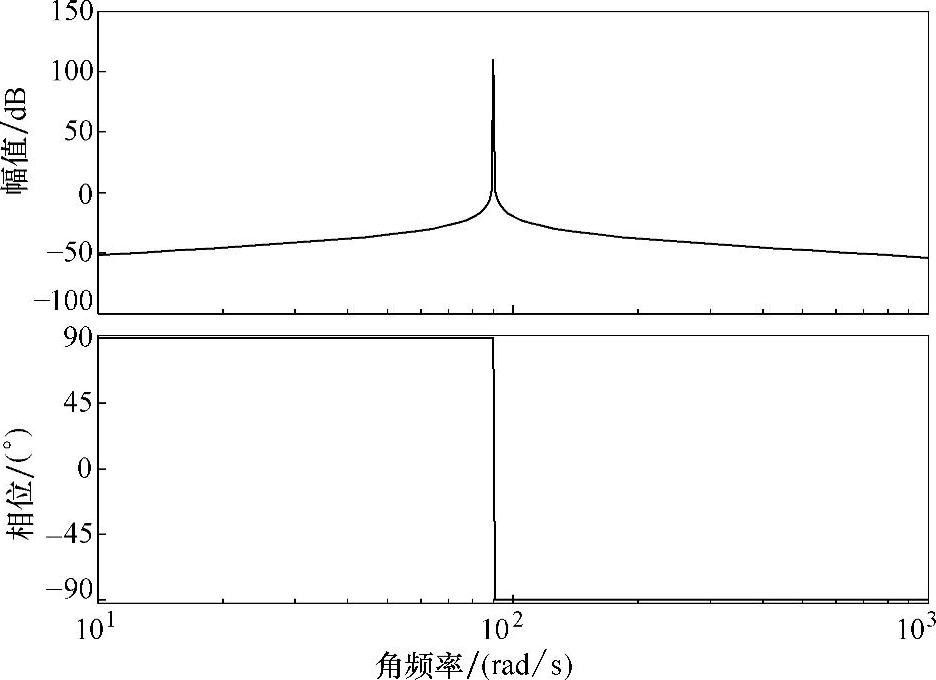
图5-43 谐振调节器幅频特性

由图5-43可见，谐振调节器在谐振频率2f_o=90Hz处有无穷大的增益，相角为0，在谐振频率之外幅频特性迅速衰减，因此，可实现对2f_o交流信号的无静差跟踪控制。PIR调节器在谐振频率点主要有谐振调节器调节控制，谐振频率之外由PI调节器起作用。

若将PIR调节器的传递函数代入式（5-101），可得从电流给定到电流误差的闭环传递函数为

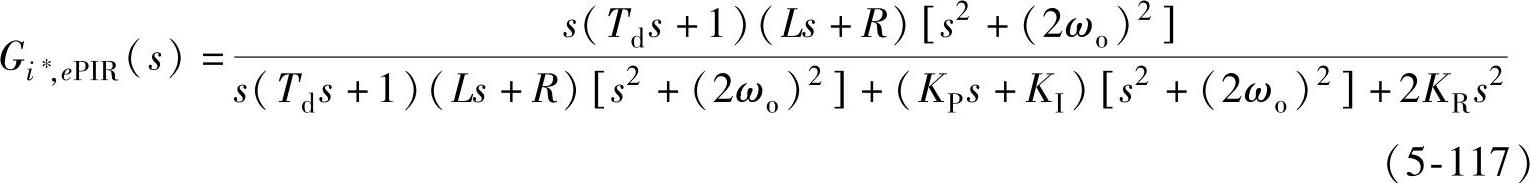
若将PIR调节器的传递函数代入式（5-102），可得从扰动到电流误差的闭环传递函数为

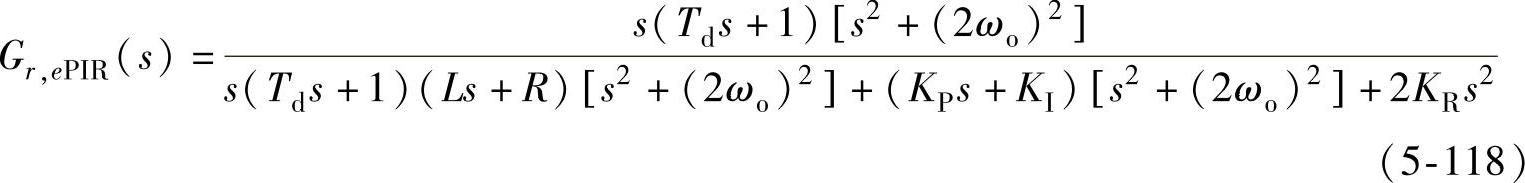
假设电流环PIR调节器的参数选取适当，即式（5-117）和式（5-118）闭环传递函数的极点均位于复平面的左半平面（不包括虚轴）。

当电流给定值和交叉耦合扰动的数学模型均为阶跃函数时，可得到电流误差响应均未引入额外的极点，符合拉氏变换终值定理条件，因此由拉氏变换终值定理可得到系统的稳态误差为

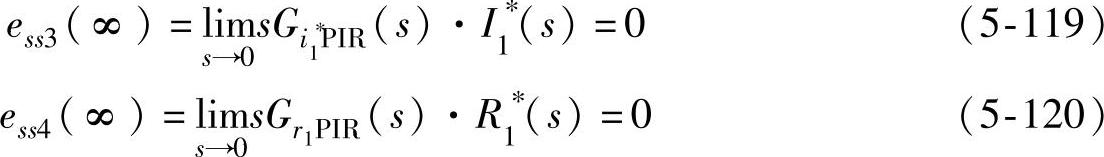
当电流给定值和交叉耦合扰动为2ω_o交流分量时，同理可得电流误差响应信号未引入额外的极点，则由拉氏变换终值定理可得系统稳态误差为

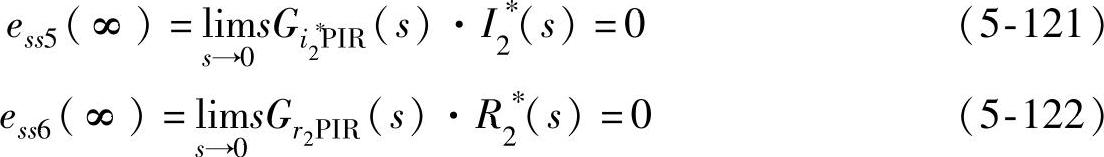
由以上分析可知，三相PWM整流器带单相H桥负载时，电流环采用PIR调节器能对直流分量和2ω_o交流分量进行控制，使PWM整流器具有较好的稳态性能^[176]。而且当电流环不加前馈解耦环节时，虽然动态性能会受到一定的影响，但其稳态性能不受影响。这样系统不受电感参数变化的影响，更有利于功率单元的通用性。电流环采用PIR调节器的三相PWM整流器带单相H桥负载控制框图如图5-44所示。

3.仿真实验与分析

图5-45所示为三相PWM整流器带单相H桥负载采用负载功率前馈加电流环PIR调节器控制策略的系统仿真模型。设H桥的输出频率f_o=45Hz，系统仿真参数与采用PI调节器时相同，系统仿真时间为0.5s，采用变步长离散算法。仿真波形如图5-46～图5-48所示。

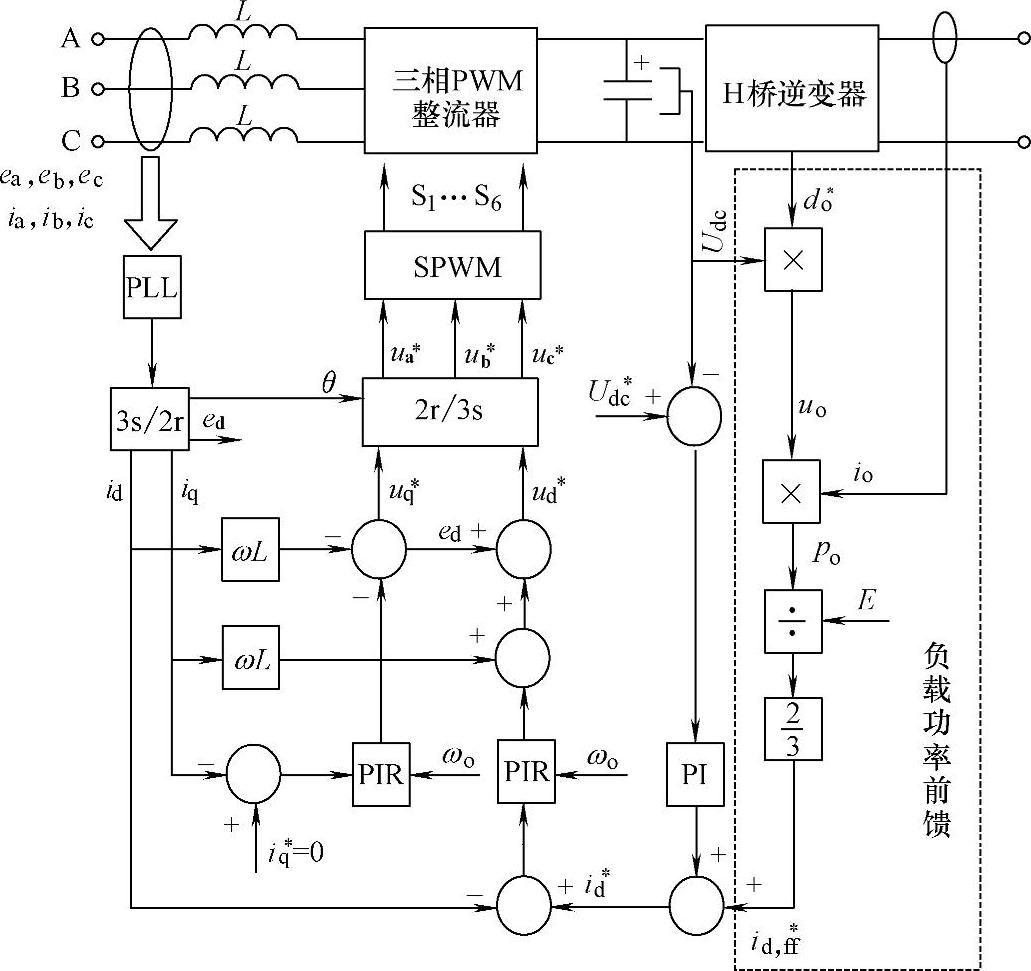
图5-44 负载功率前馈加电流环PIR调节器控制框图

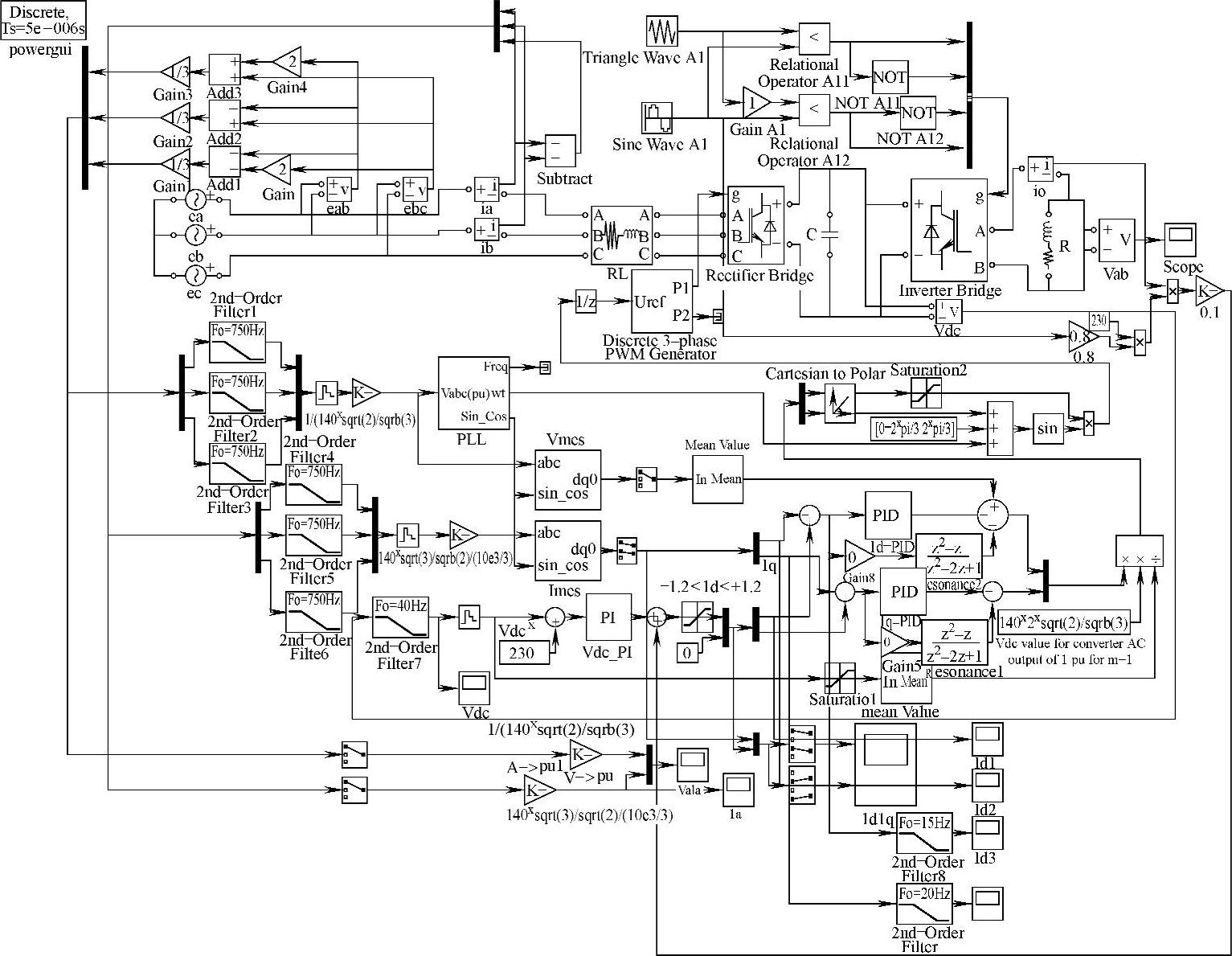
图5-45 负载功率前馈加电流环PIR调节器控制策略系统仿真模型

图5-46所示为采用负载功率前馈加电流环PIR调节器控制的系统母线电压整体与局部放大波形。由整体波形图可见，母线电压维持在给定值230V，电压基本平稳；由放大波形可见其波动峰峰值为2V，与前面介绍的负载功率前馈控制比较，波动幅度减小。

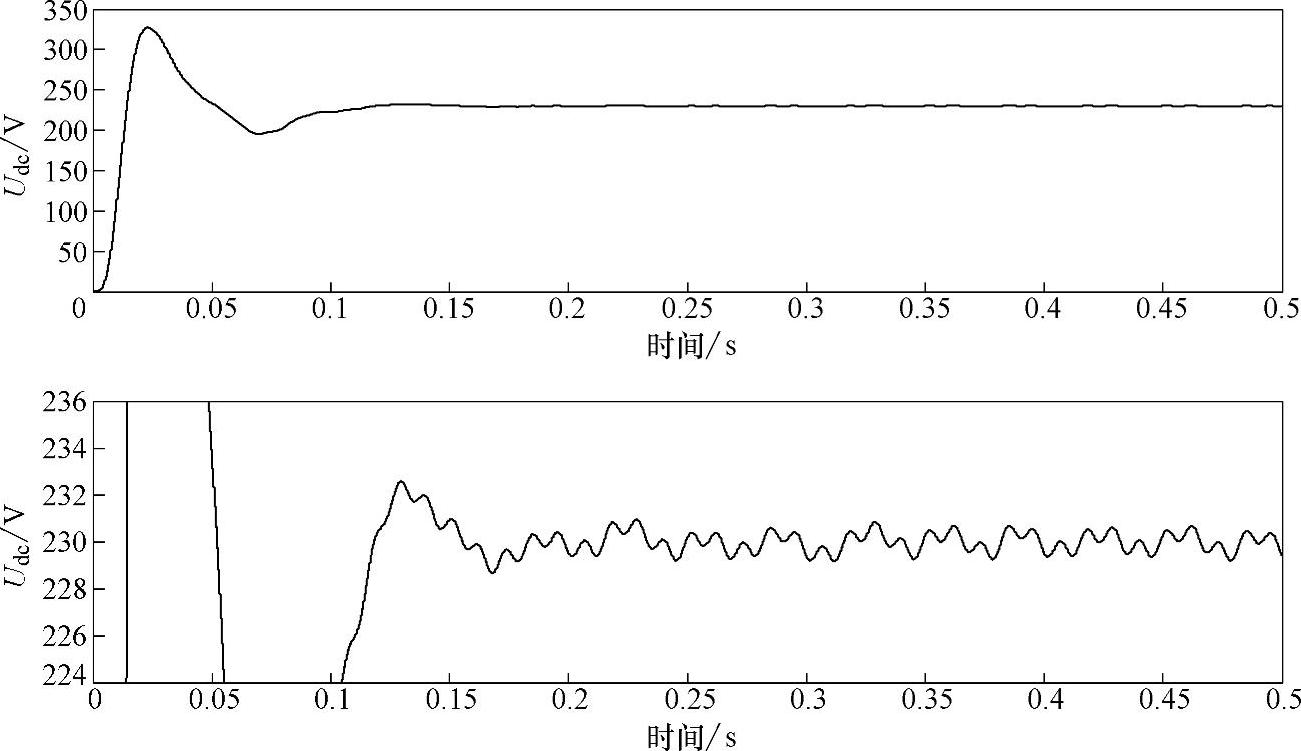
图5-46 负载功率前馈加电流环PIR调节器控制策略的系统母线电压仿真波形

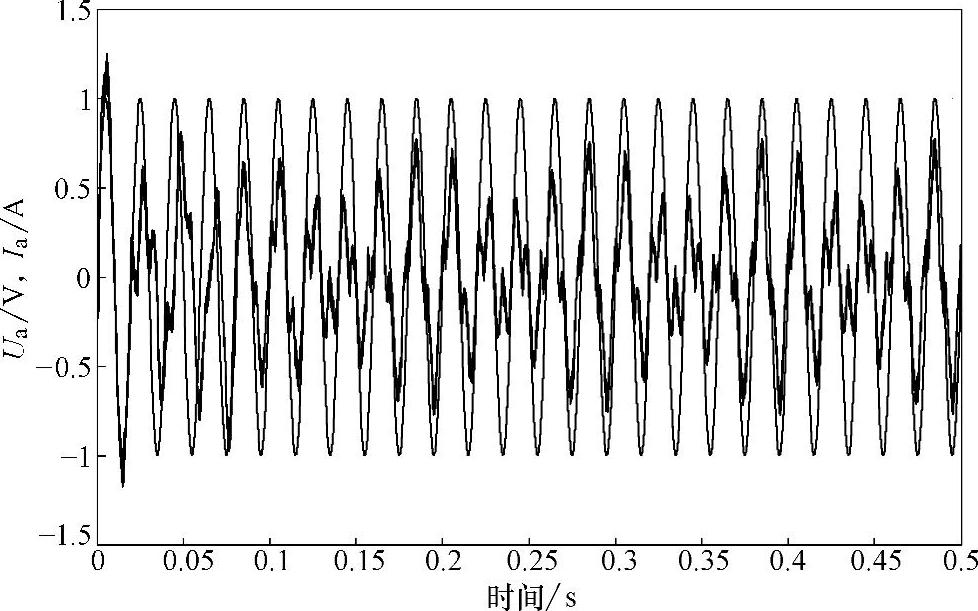
图5-47 负载功率前馈加电流环PIR调节器控制策略的系统相电压与相电流仿真波形

图5-47所示为网侧相电压与相电流仿真波形。由图可见，相电压与相电流同相位，电流环响应速度较快。其中相电流波形质量较差，这是因为通过负载前馈完全补偿掉输出功率的波动后，虽然实现了直流母线电压的稳定，但有功d轴电流给定值存在2倍频波动，会在三相电流中引入谐波，从而造成三相电流波形变差。

图5-48所示为采用负载功率前馈加电流环PIR调节器控制策略系统有功电流与无功电流波形。将图5-48与图5-32（传统VOC控制策略有功电流与无功电流仿真波形（加低通滤波器））相比较可发现，图5-48中的d轴电流误差值维持在0轴附近，基本平稳，d轴有功电流跟踪效果明显；并且q轴电流也没有明显的波动。由于d轴电流控制效果的改善，直流母线电压波动幅度也进一步减小。

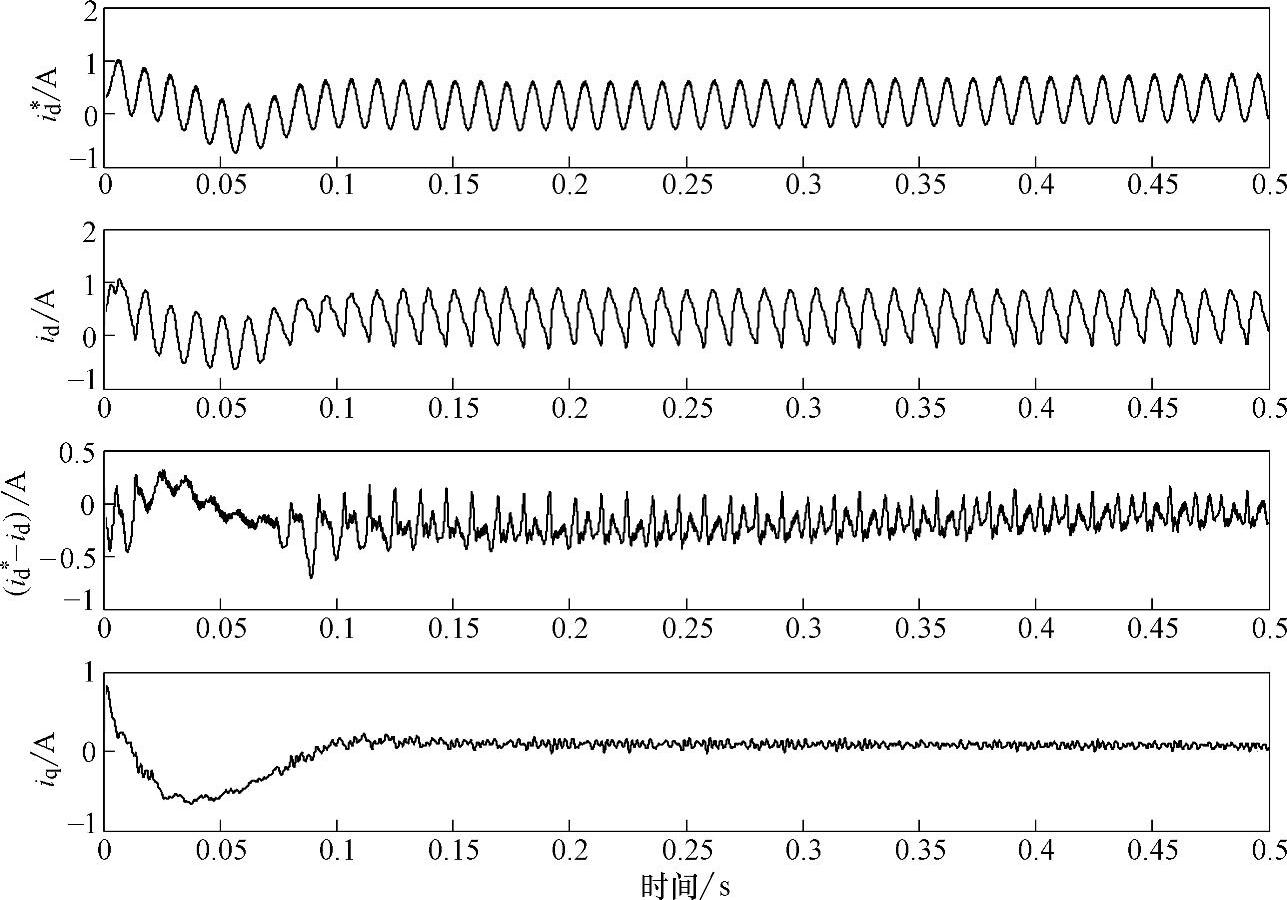
图5-48 负载功率前馈加电流环PIR调节器控制策略的系统有功电流与无功电流仿真波形

通过上述仿真实验，进一步验证了在三相PWM整流器带单相H桥负载系统中电流环采用PIR调节器的优势。