单相全桥整流功率单元的能量回馈控制策略优化

为表示能量回馈功率单元与电网的关系，图5-3所示的带有单相全桥整流的功率单元拓扑可进一步表示成图5-12。

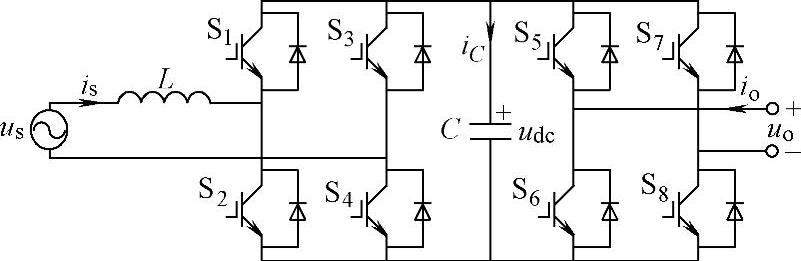
图5-12 带有单相全桥整流的功率单元电路结构图

关于带有单相全桥整流的功率单元能量回馈控制策略，参考文献[161]介绍了采用电压外环和电流内环的双闭环控制结构，其控制框图如图5-13所示。

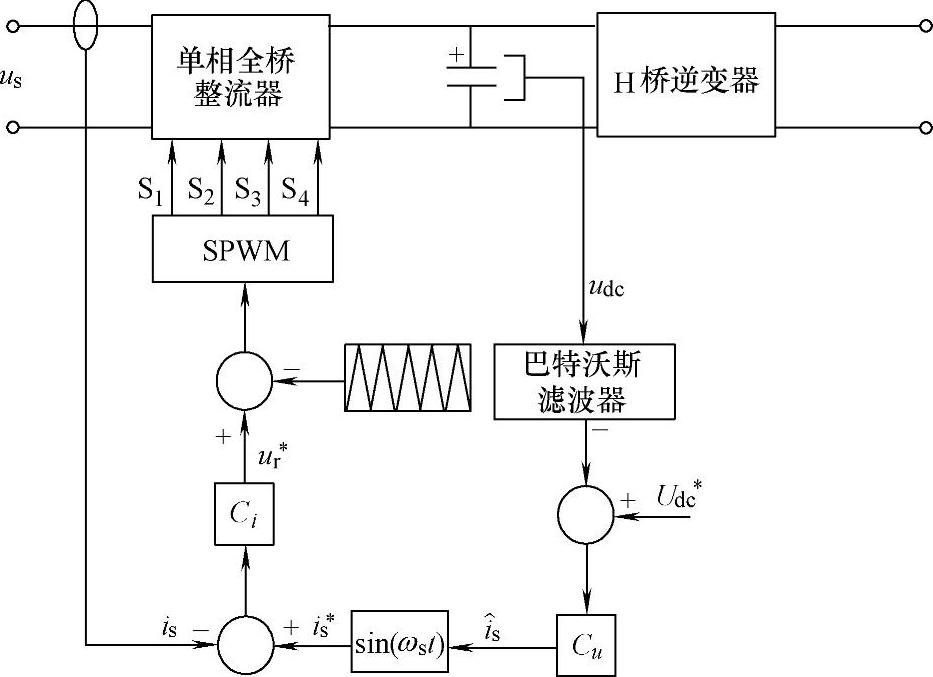
图5-13 带有单相全桥整流的功率单元能量回馈控制框图

在图5-13中，直流母线电压经采样、滤波后，与给定值U^∗_dc作比较得到反馈信号，反馈信号经电压调节器C_u得到电流给定值的幅值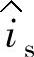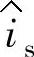，与输入电压u_s同频同相的正弦信号sin（ω_st）相乘得到电流控制环的给定电流i^∗_s，给定电流i^∗_s与实际输入电流i_s作比较经电流调节器C_i得到整流器的给定调制波电压u^∗_r，最后采用SPWM调制策略获得整流器功率器件的驱动脉冲。

假设初始状态的功率单元输入电流i_s与输入电压u_s为同频同相的正弦信号，则功率单元瞬时输入功率为

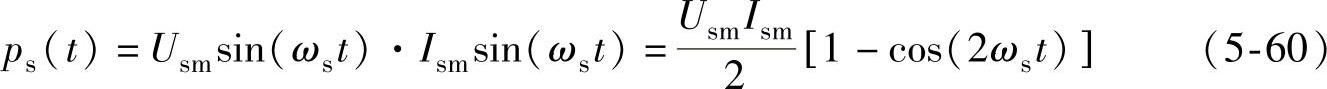
式中，U_sm、I_sm分别为功率单元输入电压、输入电流的峰值，ω_s为电网角频率。

由式（5-60）可见，瞬时输入功率由两个分量组成，即常量（有功功率）和2倍频脉动分量（无功功率），且它们的幅值相等。输入功率的2倍频波动会引起直流母线电压波动，如果直流母线电压2倍频波动反馈到控制系统，给定电流i^∗_s将会产生ω_s和3ω_s角频率的谐波。若在母线电压测量时加巴特沃斯滤波器，可在反馈通道消除母线电压的2倍频波动，则给定电流不会产生ω_s和3ω_s角频率的谐波^[166]。

再假设输出电流i_o是角频率为ω_o的正弦量，则功率单元瞬时输出功率为

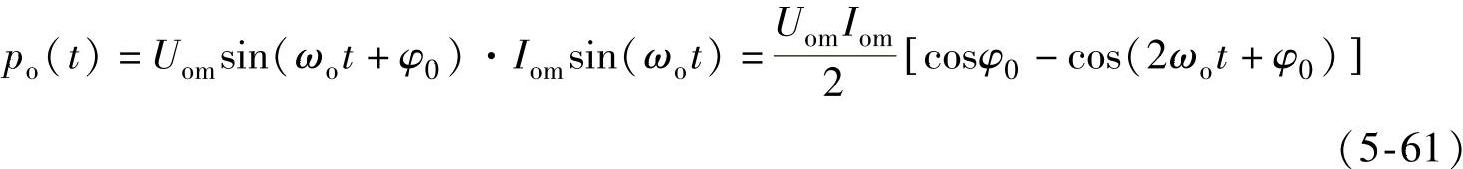
由式（5-61）可见，瞬时输出功率也包含2倍频脉动分量。

由于直流母线电压调节器是保证对电容电压实现零稳态误差控制，因此瞬时输入、输出功率应相等。当满足这一条件时，直流母线电压才能恒定不变且没有波动，否则电容所吸收的功率为

p_C（t）=p_s（t）-p_o（t） （5-62）

同时，电容的瞬时功率也可表示为

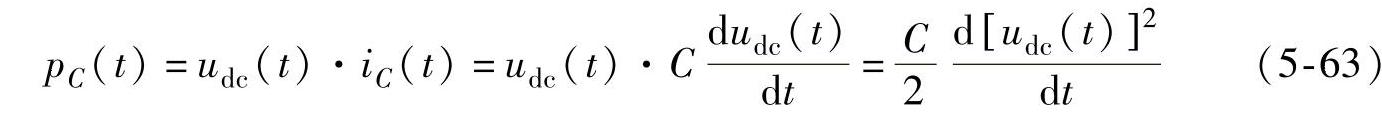
因此，电容电压为

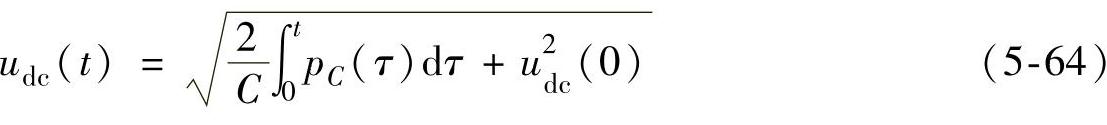
式中，u_dc（0）为母线电压给定值U_dc。

运用泰勒公式

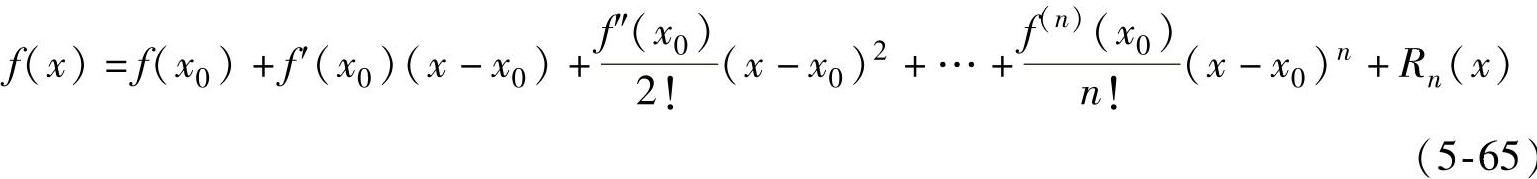
将式（5-64）展开，并取前两项可得

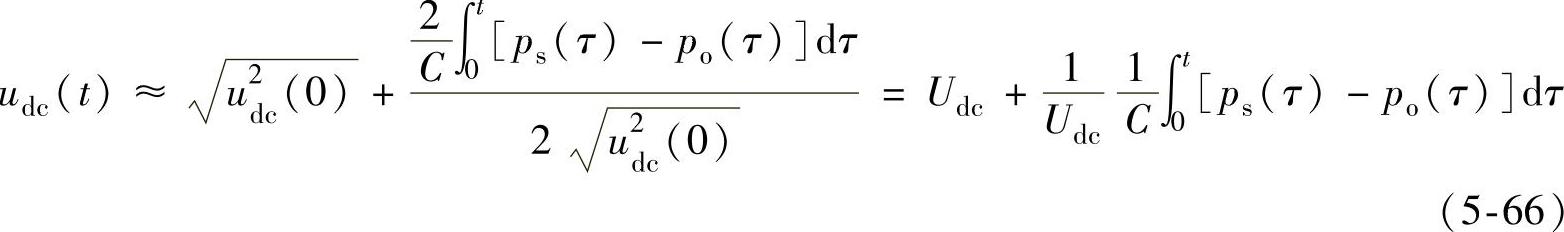
即有

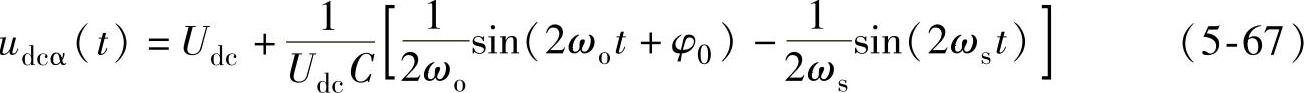
因此，电压环PI调节器输出电流为

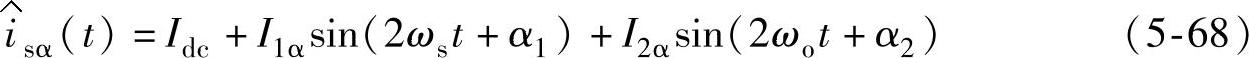
故电流给定为

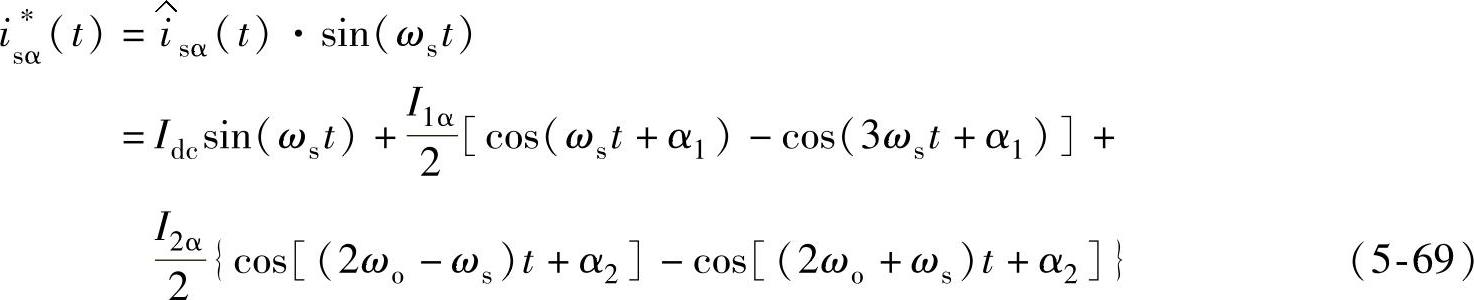(www.xing528.com)

前面提到母线电压中存在的2ω_s谐波可由巴特沃斯滤波器消除，因此，电压调节器输出电流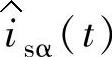不含2ω_s分量，即式（5-68）可简化为

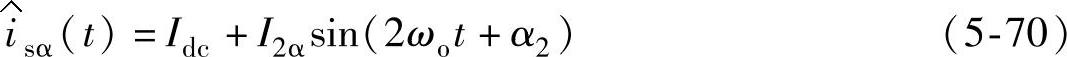
因此，式（5-69）电流给定可等效为

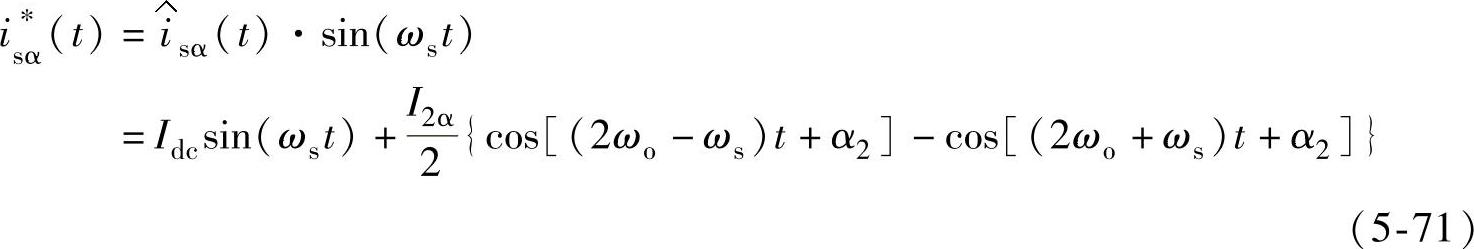
在带有单相全桥整流的功率单元中，由图5-13所示的控制框图可知电流给定为

又由式（5-71）可知，电流给定不是纯正弦量，而是包含另两个低频量，即2ω_o±ω_s。

因为电流调节器要保证对给定电流i^∗_s的跟踪控制，所以输入电流i_s不是纯正弦量，而是包含三个低频量，即ω_s、2ω_o±ω_s。

在此条件下，瞬时输入功率则为

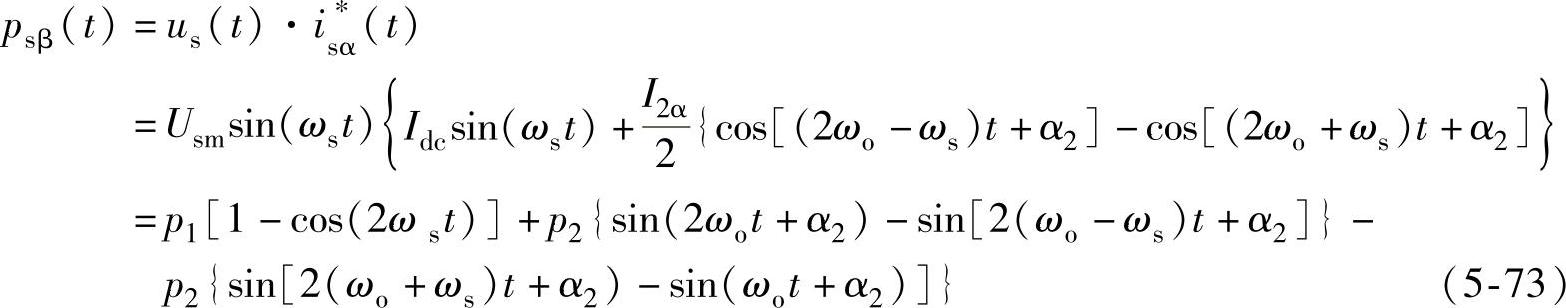
式中，p₁=U_smI_dc/2；p₂=U_smI_2α/4。

因此，由式（5-66）得直流母线电压为

u_dcβ（t）=U_dc-U_1βcos（2ω_st）+U_2βsin（2ω_ot+α₂）+U_3βsin[2（ω_o-ω_s）t+α₂]-U_4βsin[2（ω_o+ω_s）t+α₂]-U_5βsin[（ω_ot+α₂）] （5-74）

由上式可知，直流母线电压中含有谐波为2ω_s，2ω₀，2ω₀±2ω_s。母线电压中2ω_s谐波可由巴特沃斯滤波器消除，不会引入电压闭环反馈通道，因此，进一步得

到电流控制环的给定电流为

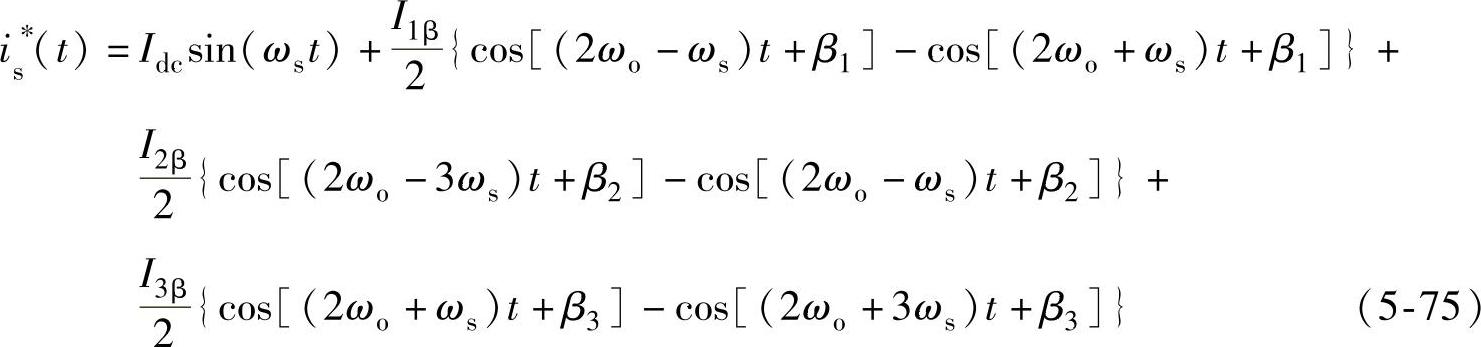
由式（5-75）知功率单元输入电流谐波为2ω_o±ω_s，2ω_o±3ω_s，另外由于PI调节器的低通滤波作用使得高次谐波均被消除。为了实现高输入功率因数，则需要对给定电流i^∗_s在角频率ω_s处零稳态误差跟踪控制，电流调节器在角频率ω_s处增益应为无穷大，即其传递函数必须有两个谐振极点±jω_s；同时，为了达到快速响应，电流调节器必须有比例增益，因此，可以选择普通的二阶谐振调节器，其传递函数为

对以图5-12为基本功率单元构成的3单元串联变频器为例进行分析^[167]，前端采用普通的隔离变压器，其整体结构如图5-14所示。

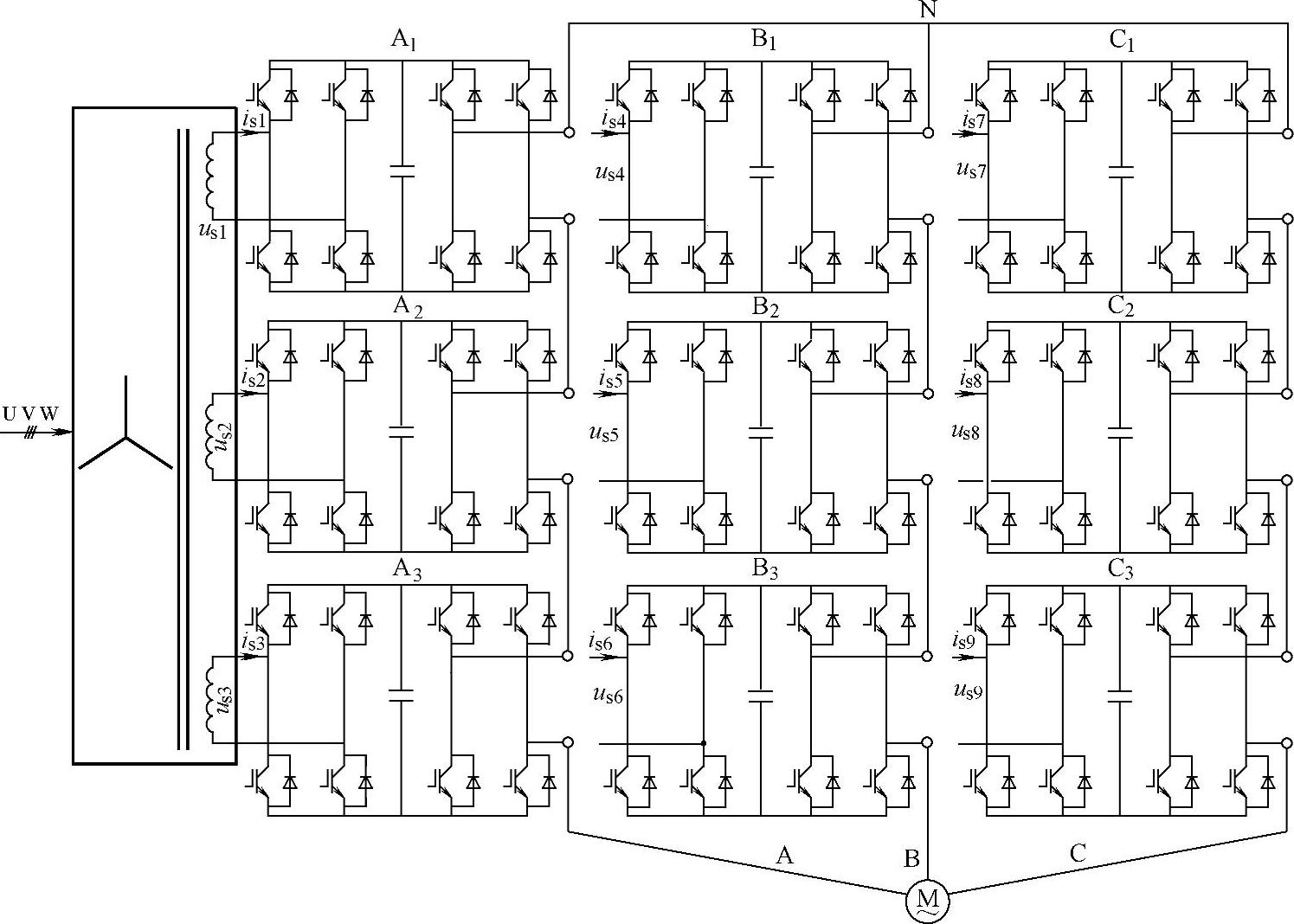
图5-14 带有单相全桥整流功率单元的三单元串联变换器结构图

由上述分析得功率单元输入电流中存在2ω_o±ω_s，2ω_o±3ω_s谐波，但是功率单元级联时，隔离变压器一次侧输入电流为

由式（5-75）可知，功率单元A1输入电流为

i_s1（t）=I_dcsin（ω_st）+I₁cos[（2ω_o-ω_s）t+δ₁]+I₂cos[（2ω_o+ω_s）t+δ₂]+I₃cos[（2ω_o-3ω_s）t+δ₃]+I₄cos[（2ω_o+3ω_s）t+δ₄] （5-78）

另外，由功率单元的级联方式可知，功率单元输入电流i_s4和i_s7相对i_s1相移分别为（ω_ot-2π/3）和（ω_ot+2π/3），则功率单元B1和C1的输入电流分别为

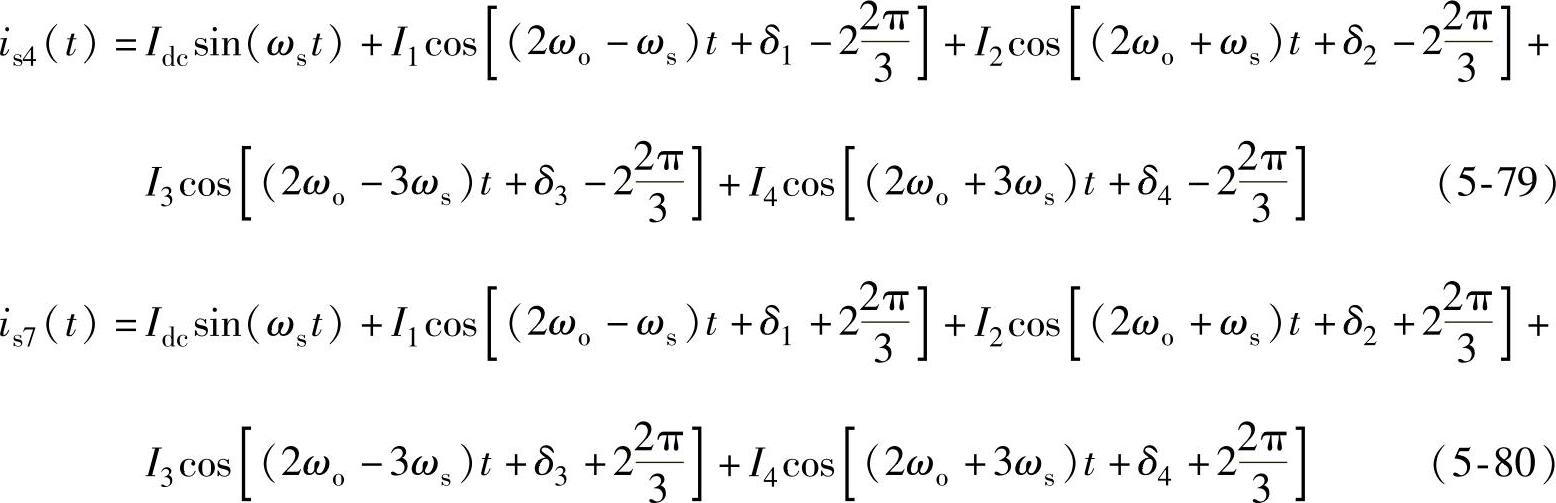
将式（5-78）～式（5-80）相加可得隔离变压器一次侧输入电流为

i_U（t）=3I_dcsin（ω_st） （5-81）

由式（5-81）可见，通过隔离变压器与功率单元间合适的互联关系，功率单元输入电流中的低次谐波电流被消除，变压器一次侧输入电流为不含有谐波分量的纯正弦波形。因此，隔离变压器的U相、V相和W相二次侧应当具有相同的绕组数；为了减小耦合至隔离变压器一次侧（即电网侧）的电流谐波，变换器同一级的A相、B相和C相功率单元（例如A1、B1和C1单元）必须连接到隔离变压器的同一相二次绕组。为了保证变压器一次侧三相输入电流平衡，这种结构要求变换器每相的级联数必须是3的整数倍。采用零稳态误差输入电流控制就无需变换器同一级的A相、B相和C相功率单元连接到隔离变压器的同一相二次绕组，也就没有对级联单元数的限制^[168]。参考文献[161]和[167]对隔离变压器与功率单元整流侧采用另一种联结方式，并把应用于级联型H桥逆变侧的多载波水平移相PWM技术应用于功率单元整流侧，既可消除隔离变压器一侧电流中的低次谐波，又可消除开关频率处的谐波，提高等效开关频率。但是，由于带有单相全桥整流功率单元的整流侧和逆变侧都是H桥，功率的瞬时值均包含较大的低频脉动分量，这些脉动功率的能量都必须由直流母线电容吸收，所以该拓扑的直流母线电容需要较大的容量。