带有三相半桥整流的功率单元能量回馈控制策略

研究电力电子变换器的控制策略，主要关注的是受控对象的基波特性，通常假设电压电流高次谐波均可忽略。为表示能量回馈功率单元与电网的关系，图5-2所示的带有三相半桥整流的功率单元拓扑可进一步表示成如图5-9所示的结构。

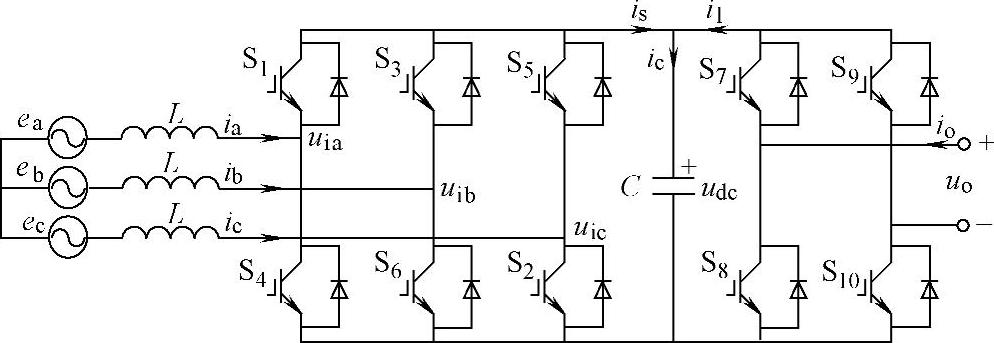
图5-9 带有三相半桥整流的功率单元电路结构图

设图5-9所示的功率单元输入电压、电流同相位，则输入电压为

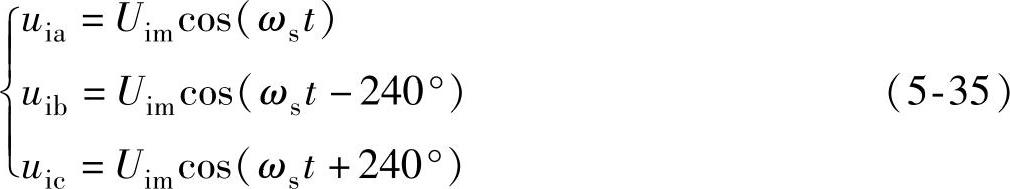
输入电流为

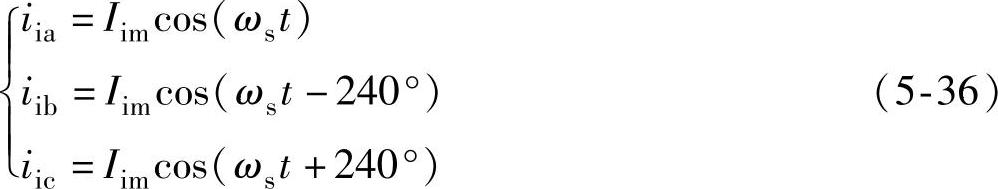
式中，U_im、I_im分别为功率单元三相输入电压、电流的峰值，ω_s为电网角频率。

设功率单元的负载为感性负载，且只考虑基波分量，则功率单元的输出电压为

u_o=U_mcos（ω_ot） （5-37）

功率单元的输出电流为

i_o=I_mcos（ω_ot-φ） （5-38）

式中，U_m、I_m分别为功率单元输出电压、电流的峰值，ω_o为输出电压角频率，φ为负载的功率因数角，则可得到功率单元瞬时输出功率为

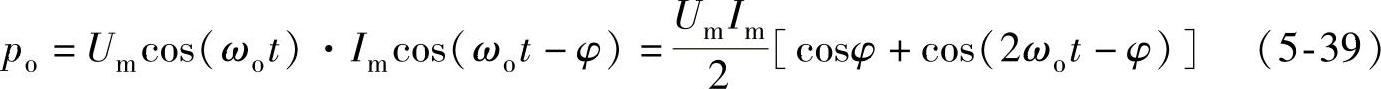
由于功率单元逆变侧为单相H桥结构，为了便于分析，对功率单元的逆变侧输出可构造一个三相不平衡系统，其三相电压为[u_o 0 0]^T、三相电流为[i_o 0 0]^T。在等功率坐标变换条件下，又可将电压、电流由静止坐标系abc变换到静止坐标系αβ0，则有

由pq瞬时功率理论^[165]知，所构造的三相不平衡功率单元瞬时输出功率为

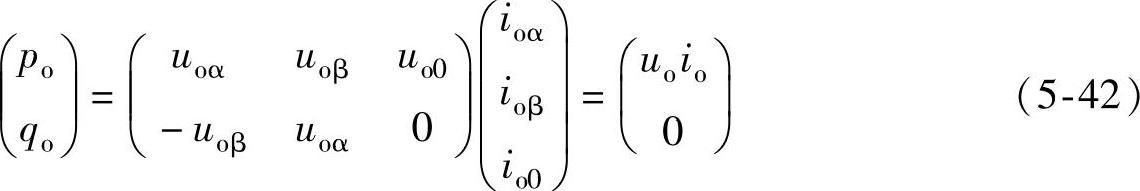
由式（5-42）可知，瞬时输出有功功率为p_o=u_oi_o，瞬时输出无功功率为q_o=0。

假设功率单元输入不存在零序分量，根据瞬时无功功率理论和“等功率”坐标变换，瞬时输入有功功率与无功功率可以表示为

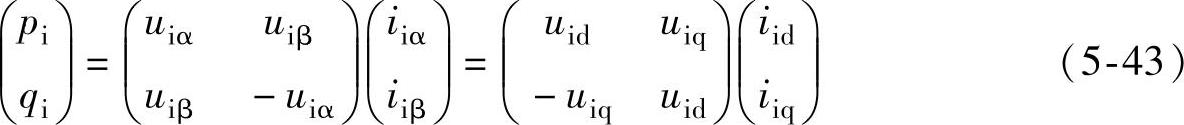
在输入输出功率相等的条件下，即

则有

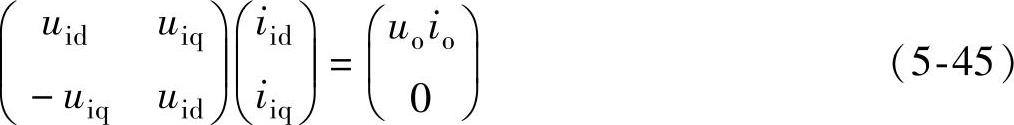
所以输入电流d、q分量的给定为

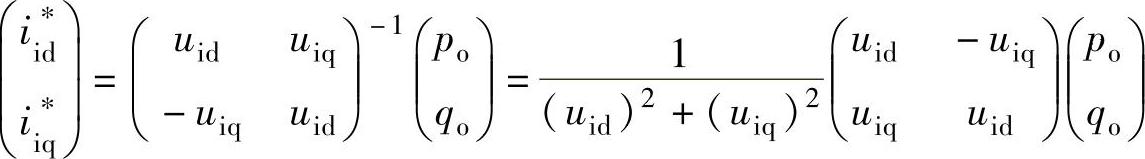
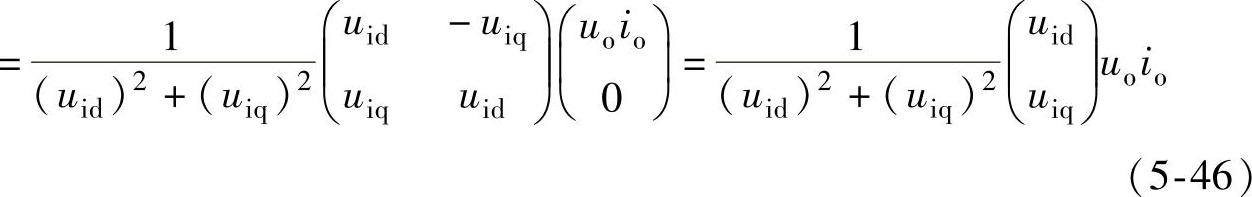
在三相静止坐标系abc下，存在

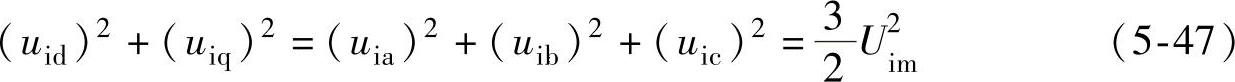
故输入电流d、q分量的给定可变换为(www.xing528.com)

而输入电流d、q分量的给定变换到三相静止坐标系abc时有

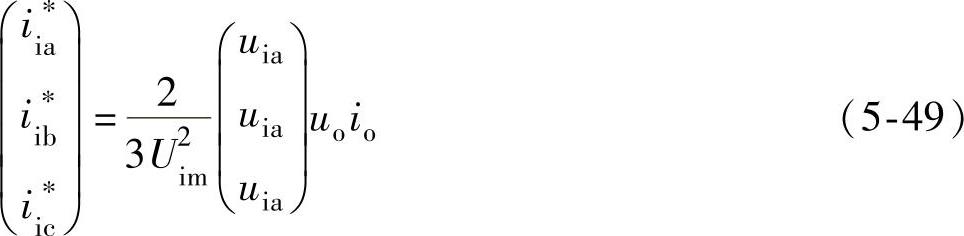
1.d、q电流控制环

在三相系统中通常u_id为常数（一般假设电网电压不畸变），u_iq为0，即

则d、q轴电流给定分量为

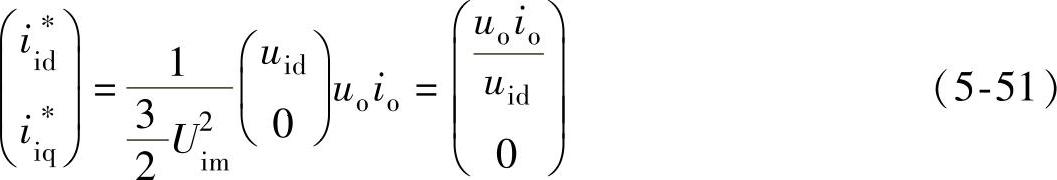
为了在不改变负载有功功率的条件下实现对输入无功功率的控制，一般取无功电流给定为一任意量I^∗_iq，因此，d、q轴电流给定分量为

2.母线电压控制环

在功率单元没有损耗的情况下，母线电容也没有能量的消耗，因此母线电压是稳定的，但由于导热和开关损耗，以及寄生电容存在等因素，实际的母线电压是存在波动的。为了维持直流母线电压恒定，现假设电路中功率损耗为Δp，则d、q轴电流分量给定为

参考文献[160]，功率单元采用负载功率前馈的双闭环控制方法，其控制框图如图5-10所示。

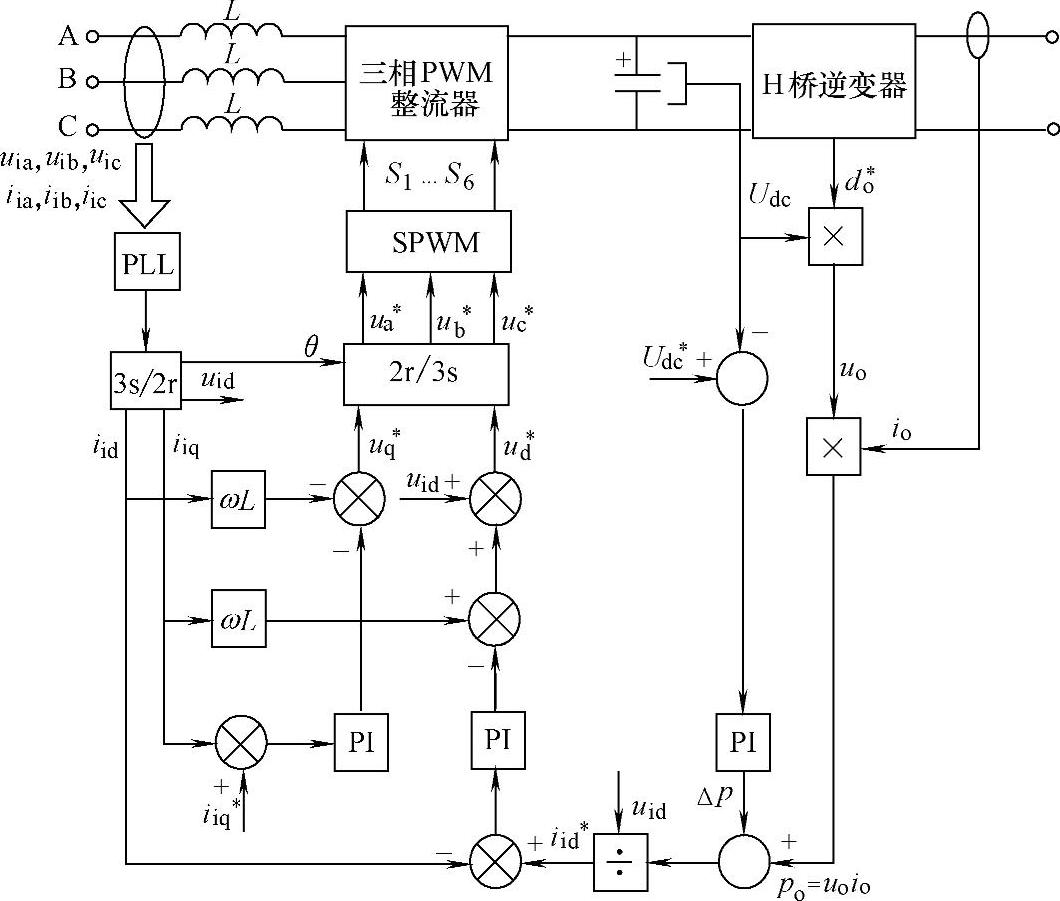
图5-10 带有三相半桥整流的功率单元能量回馈控制框图

3.交流电流谐波分析

为了了解带有三相半桥整流的功率单元能量回馈控制系统移相变压器一次侧输入电流的谐波特性，现以该功率单元拓扑的3单元串联为例，结构如图5-11所示，对一次侧输入电流谐波特性进行分析。

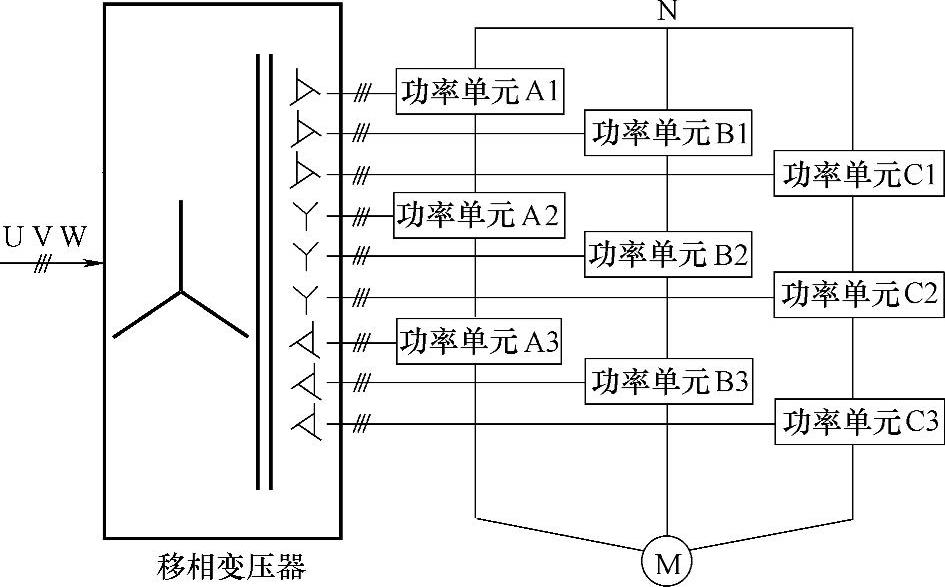
图5-11 三单元串联能量回馈变频器结构示意图

为了分析问题的方便，忽略变换器的各种损耗，即Δp=0，则由前面推导的式（5-49）可知，某一功率单元（以图5-11所示功率单元A2为例）三相输入电流分别为

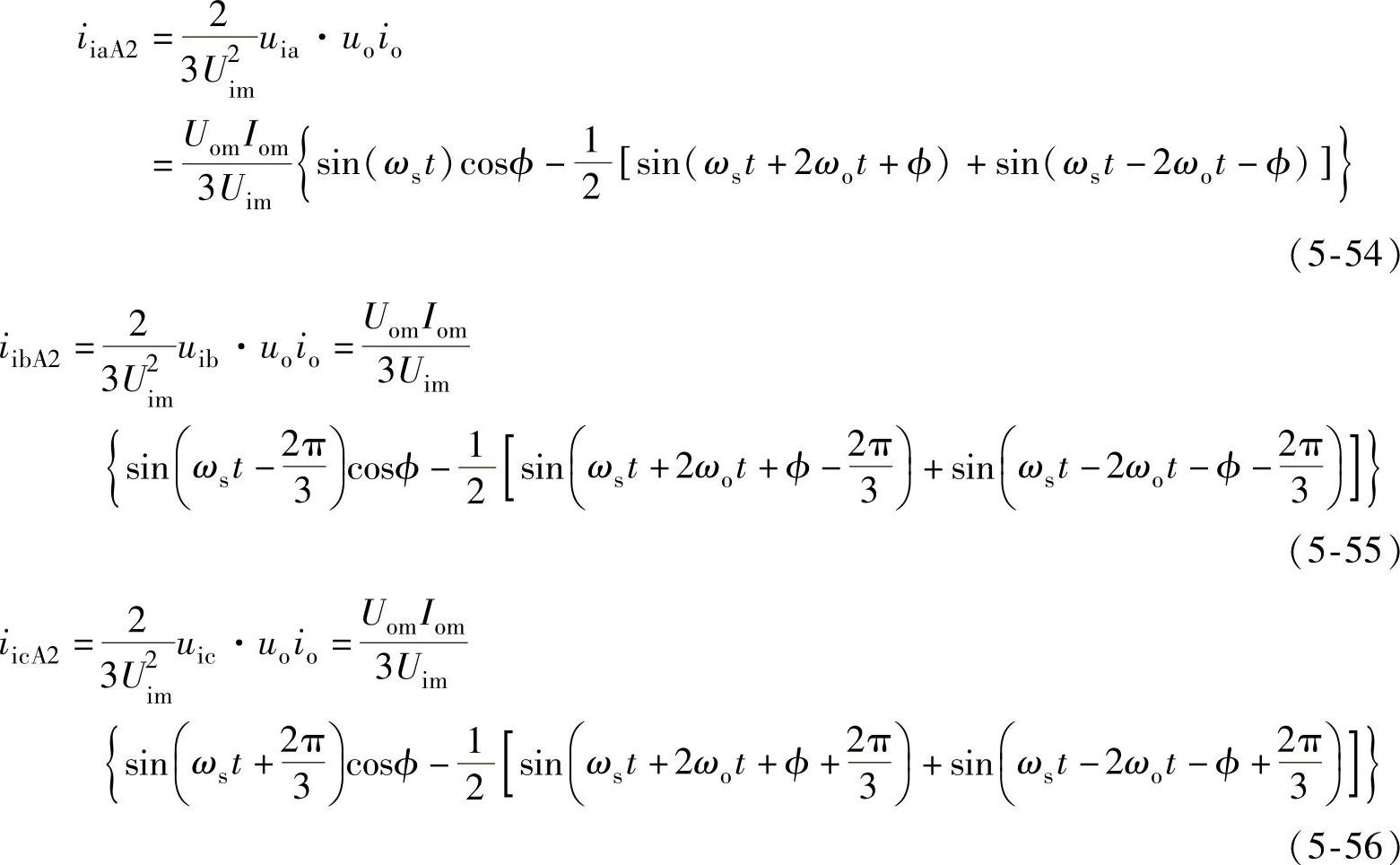
在忽略高次谐波的情况下，由式（5-54）～式（5-56）推导可知在功率单元的输入电流中主要存在ω_s+2ω_o、ω_s-2ω_o的低次谐波。

同理可以得到与A2同级的B2、C2功率单元的a相电流分别为

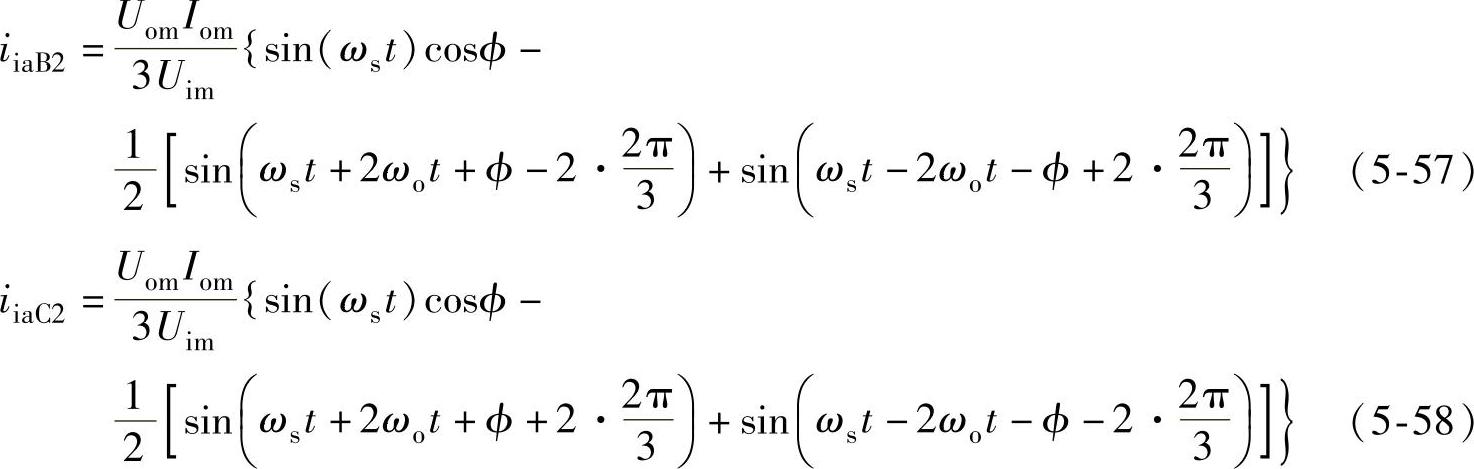
同样在B2、C2的功率单元中输入电流中也存在ω_s+2ω_o、ω_s-2ω_o的低次谐波。

将式（5-54）、式（5-57）和式（5-58）相加并折算到移相变压器的一次侧可得

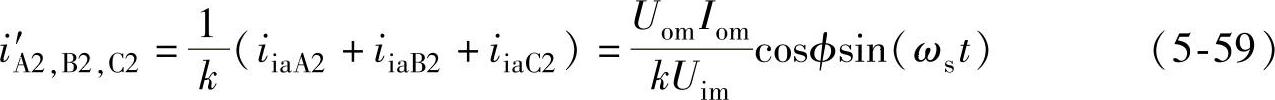
式中，k为移相变压器变压比。

通过以上分析可知，带有三相半桥整流的功率单元，移相变压器的一次侧电流与网侧电压同频同相，且不含有ω_s+2ω_o和ω_s-2ω_o低次谐波。