常用的变换原则有“等量”和“等功率”,相应的坐标变换又称“等量”坐标变换和“等功率”坐标变换[164]。
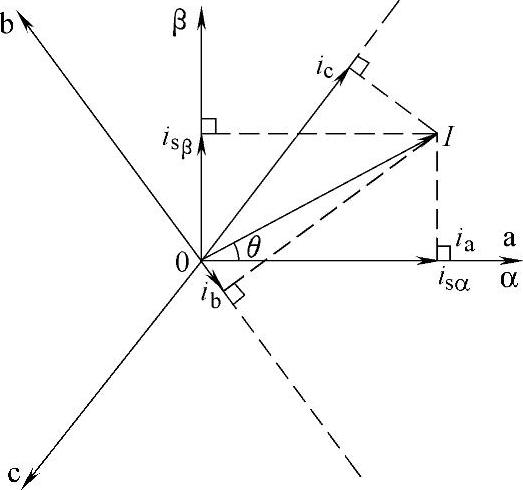
图5-63 s/2s变换示意图
1.“等量”坐标变换
所谓“等量”坐标变换是指在某一坐标系中的矢量与变换后的另一坐标系中的矢量相等的坐标变换。
1)3s/2s变换
图5-6为3s/2s变换示意图,图中a、b、c为三相对称静止坐标系,α、β为两相对称静止坐标系,两个坐标系的原点重合,并且a轴与α轴重合。
三相电流的合成矢量为I在三相对称静止坐标系内与a轴的夹角为θ,则其在三相对称静止坐标系下的投影分别为ia、ib、ic,在两相对称静止坐标系下的投影分别为isα、isβ,如图5-6所示,由图可见,三相电流的合成矢量在两相对称静止坐标系下的表达式为

三相电流的合成矢量在三相对称静止坐标系下的表达式为
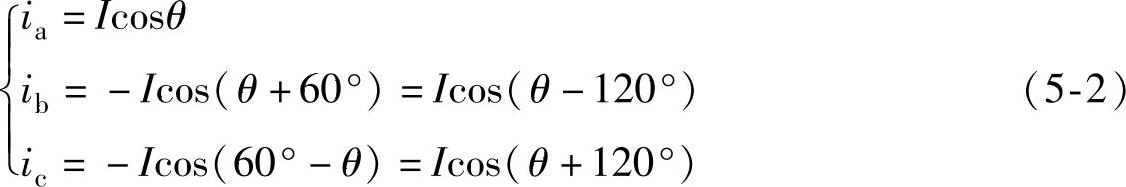
将式(5-1)代入式(5-2)可得
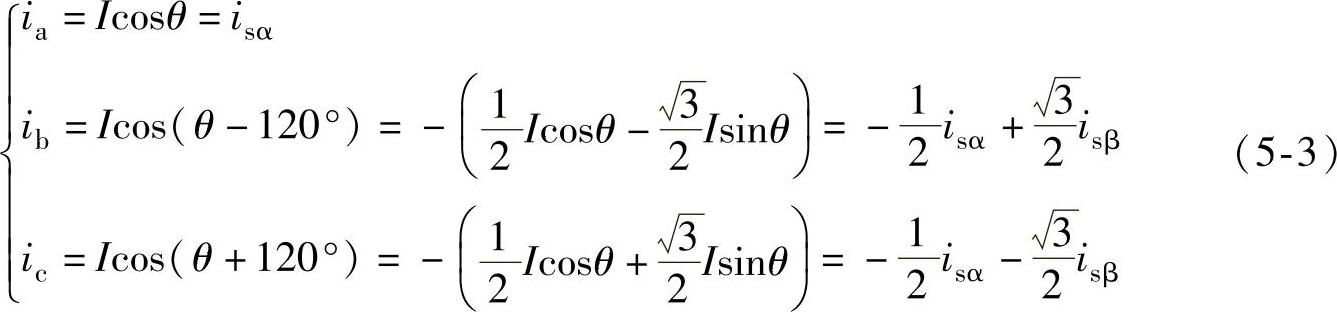
对式(5-3)做逆运算可得
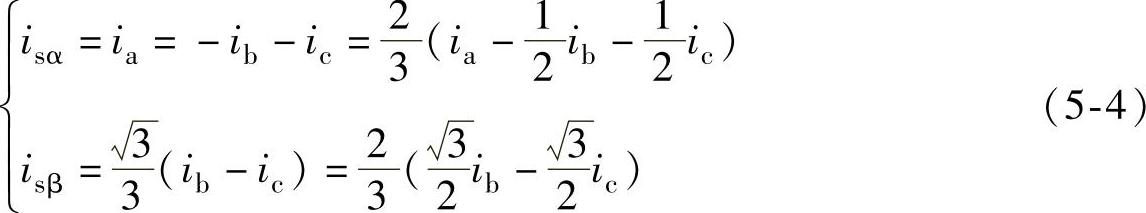
将式(5-4)用矩阵的形式表示,则有

由式(5-5)可得3s/2s变换矩阵为
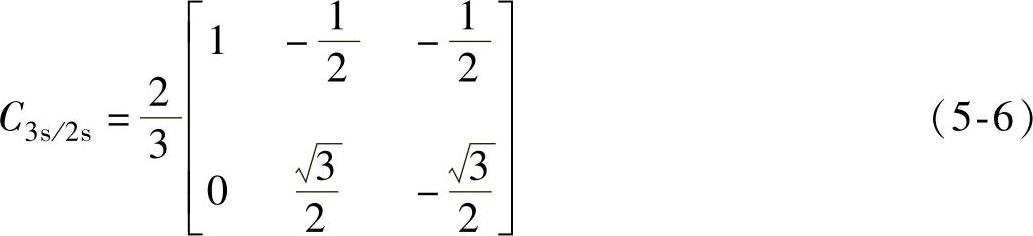
同理可推得2s/3s变换矩阵为
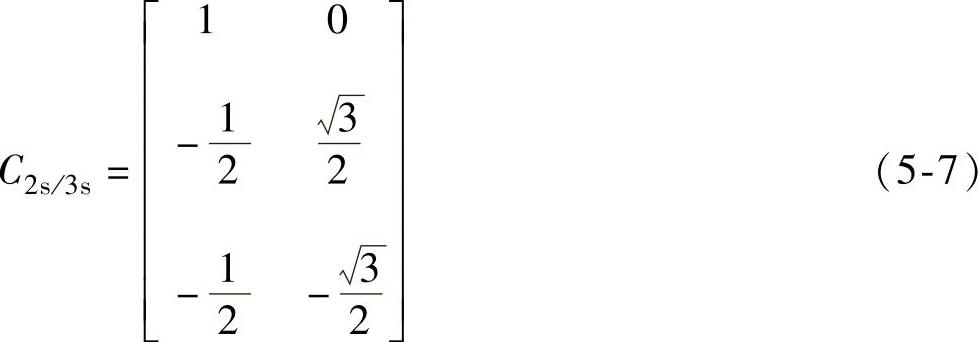
2)2s/2r变换
从静止的两相坐标系变换到旋转的两相坐标系的变换称为两相静止-两相旋转坐标变换(简称2s/2r变换),图5-7所示为2s/2r变换示意图,图中α、β为两相静止坐标系,d、q为两相旋转坐标系,两个坐标系的原点重合,设三相定子电流合成矢量I与α轴的初始夹角为θ,d轴与β轴反向的初始夹角为φ,d、q轴以电网基波角频率ω逆时针旋转。
由图5-7所示可见,定子电流在d、q轴上的分量可表示为
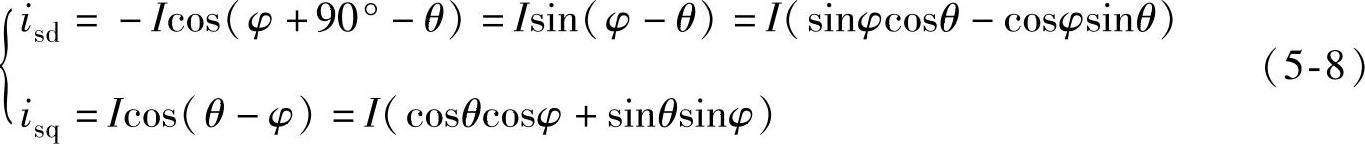
两相静止坐标系下的定子电流分量与两相旋转坐标系下的定子电流分量之间的关系为
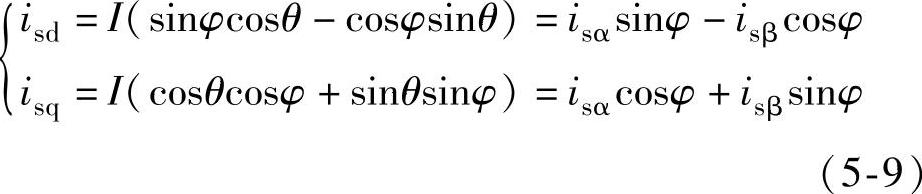
将式(5-9)用矩阵的形式表示,则有
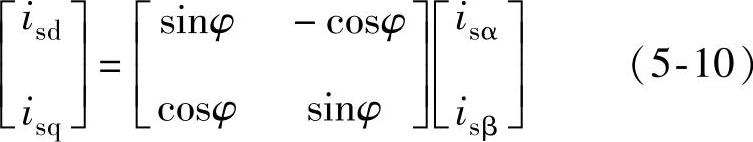
由式(5-10)可得2s/2r变换矩阵为
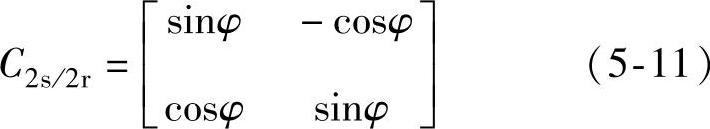
同理可推得2r/2s变换矩阵为

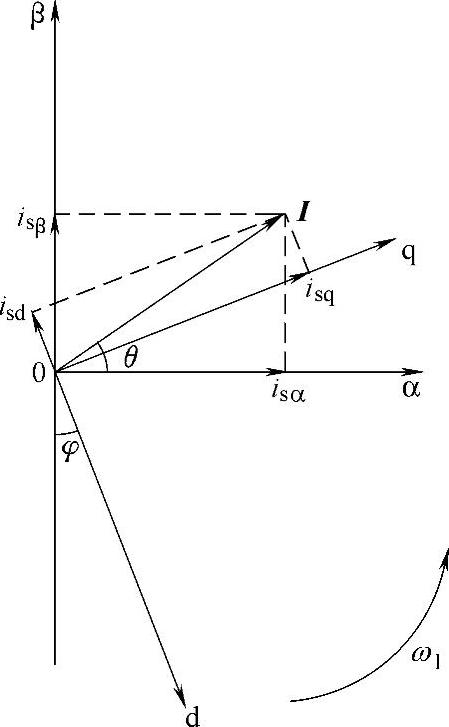
图5-7 2s/2r变换示意图
3)3s/2r变换
设在三相对称静止坐标系abc中,三相电网电动势矢量和电流矢量分别为E、I,且矢量以电网基波角频率ω逆时针旋转,两相旋转坐标系dq以角频率ω逆时针旋转,其中两相旋转坐标系dq起始位置如图5-8中虚线所示。
设两相旋转坐标系中的d轴与电网电动势矢量E同轴,即d轴按电动势矢量E定向,则E方向电流定义为有功电流分量id,q轴方向电流定义为无功电流分量iq,其中θ=ωt为坐标系旋转角度,则由图5-8所示的3s/2r坐标变换矢量图中的电流表达式为
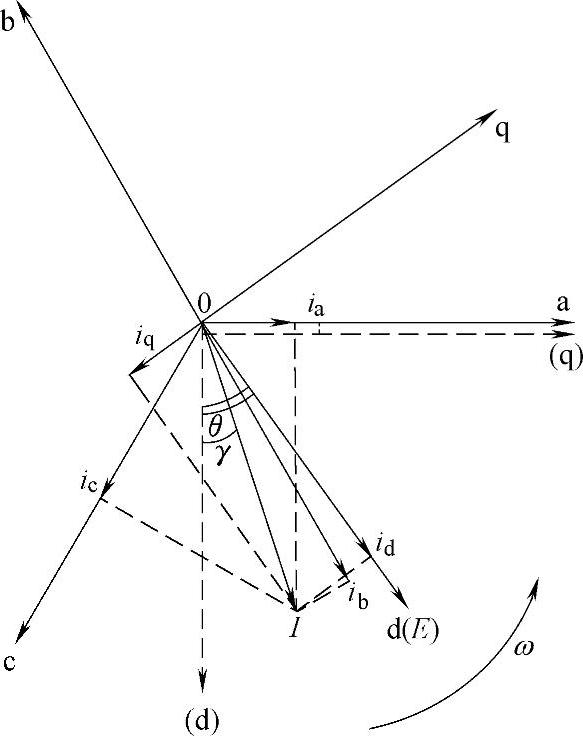
图5-8 坐标系abc与坐标系dq以及矢量分解图

由三角函数关系可得
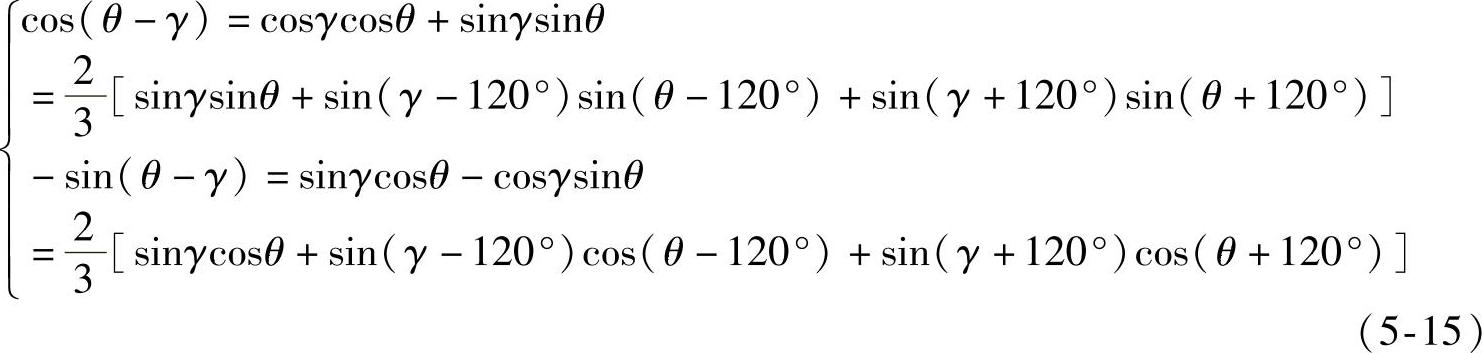 (https://www.xing528.com)
(https://www.xing528.com)
将式(5-13)、式(5-15)代入式(5-14)可得
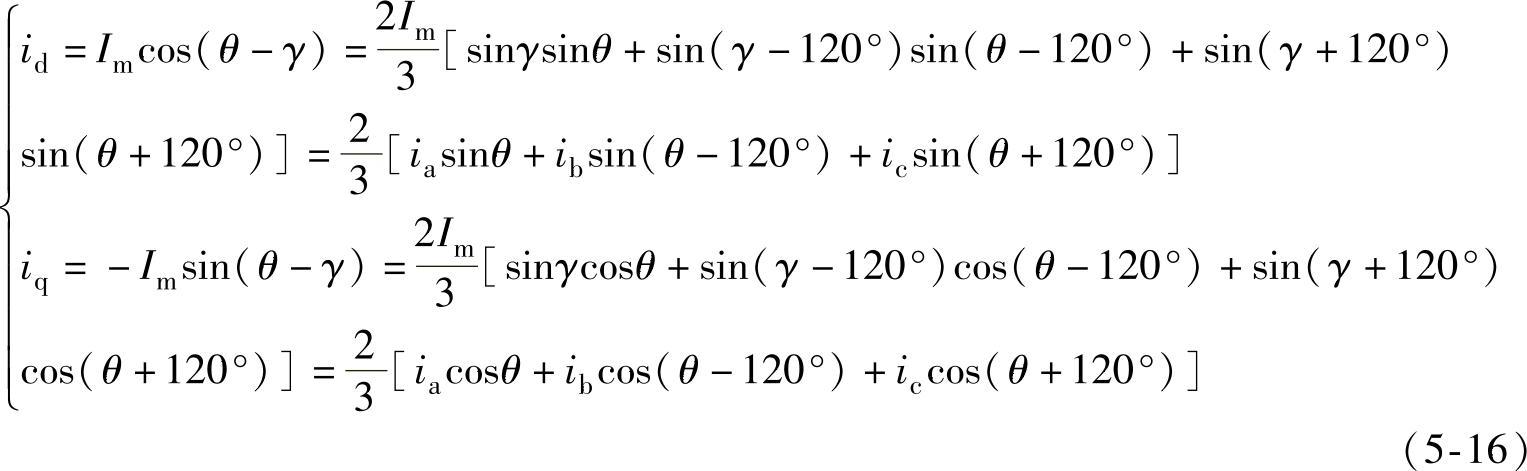
为用方阵表示坐标变换,定义零轴分量为

将式(5-16)和式(5-17)表示成矩阵等式时,则有
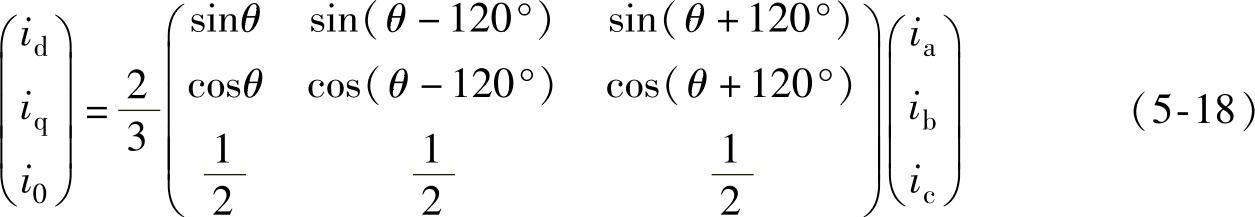
由式(5-18)可见,三相静止坐标系abc变换到两相旋转坐标系dq的变换矩阵为
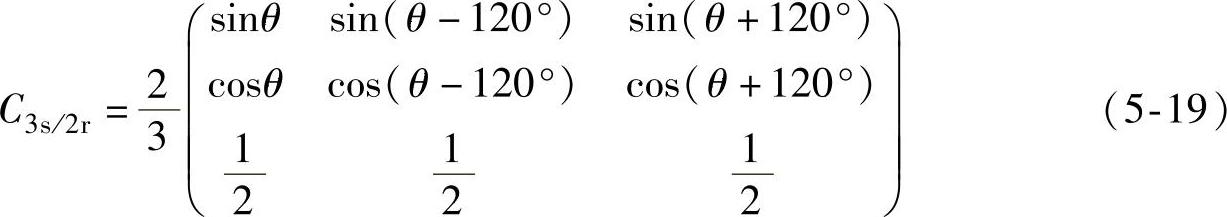
2.“等功率”坐标变换
所谓等功率坐标变换,是指坐标变换前后功率相等的坐标变换。
假设某坐标系下电压、电流矢量分别为U、I,在坐标变换后新坐标系下的电压、电流矢量分别为U′、I′,其中
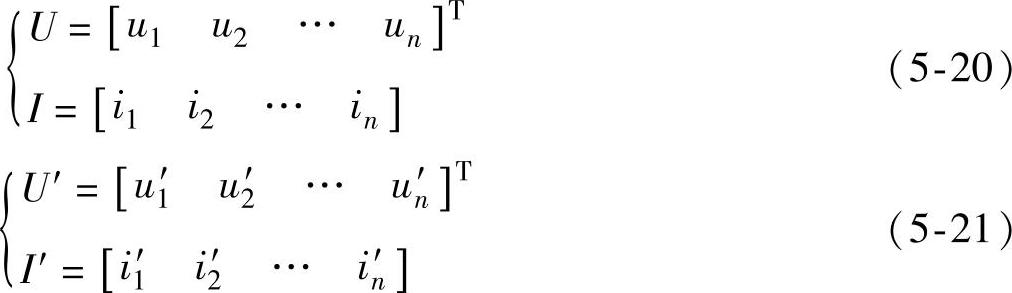
若令电压、电流变换矩阵分别为Cu、Ci,则有

当坐标变换满足“等功率”变换条件时,则有
ITU=I′TU′ (5-23)
将式(5-22)代入式(5-23)可得
ITU=(CiI′)TCuU′=I′TCTiCuU′=I′TU′ (5-24)
可见
CTiCu=E (5-25)
式中,E为单位阵。
因电压、电流矩阵描述的是同一电路拓扑结构,则有
C=Ci=Cu (5-26)
故可推得

显然,C为正交变换矩阵,即“等功率”坐标变换属于正交变换。
已知在“等量”坐标变换下,同时参考图5-6所示的坐标系,由abc坐标变换到αβ的坐标变换矩阵为
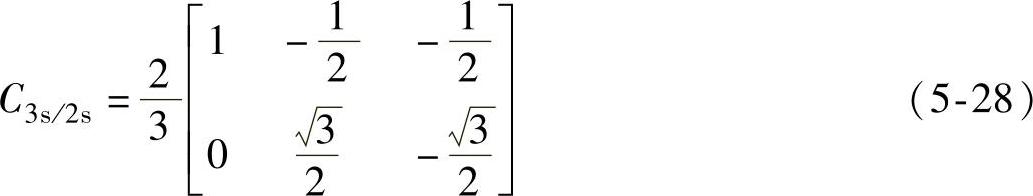
可见,式(5-28)为非正交变换矩阵。
为了建立“等量”变换与“等功率”变换之间的关系,可将非正交变换矩阵C3s/2s构造成正交矩阵C′3s/2s,即令
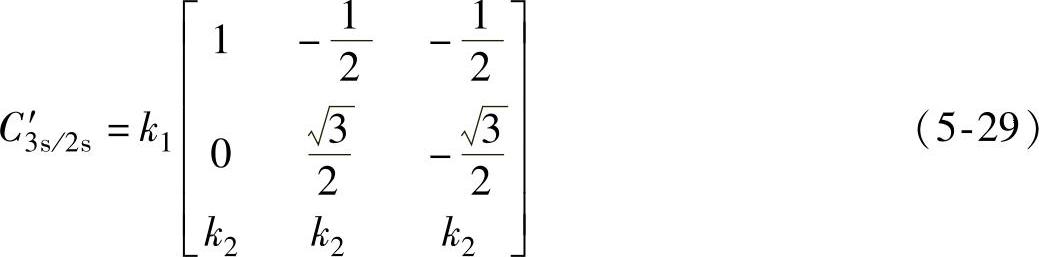
由于C′3s/2s为正交矩阵,则有
C′-13s/2s=C′T3s/2s (5-30)
因此有
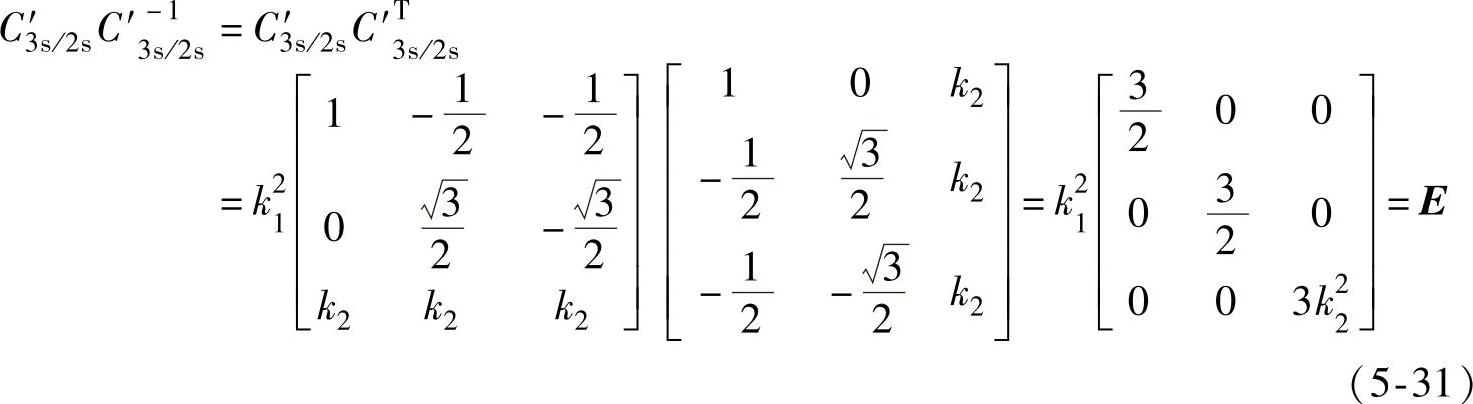
因E为单位矩阵,则

那么,在“等功率”坐标变换下,由静止坐标系abc变换到静止坐标系αβ0的坐标变换矩阵C′3s/2s为
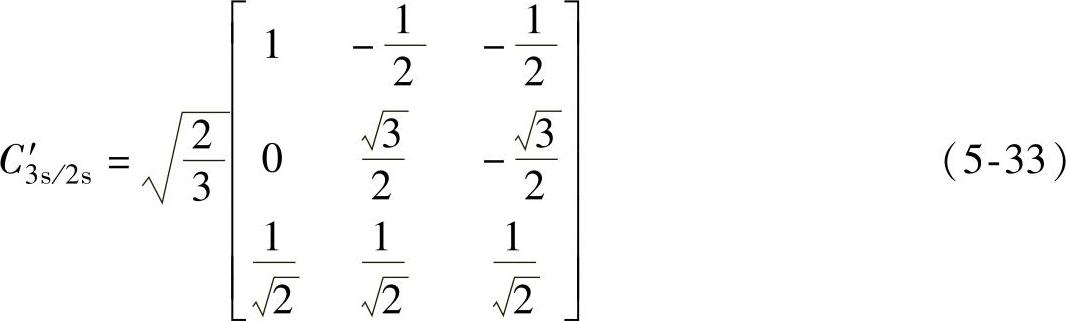
同理可得,在“等功率”坐标变换下静止坐标系abc变换到旋转坐标系dq0的坐标变换矩阵C′3s/2r为
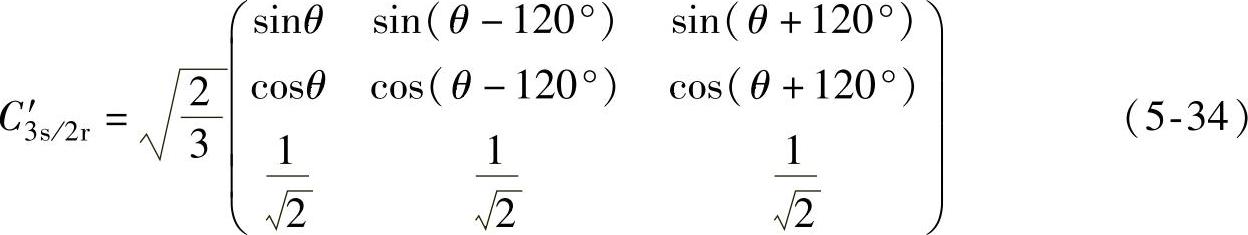
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




