【摘要】:将逻辑函数真值表中的最小项排列成矩阵,并且矩阵的横向和纵向的逻辑变量的取值按照格雷码的顺序排列,这样构成的图形称为卡诺图。卡诺图的排列特点就是具有很强的相邻性。所以,四角的最小项也都是相邻的。从图2.6.1可以看出,随着逻辑函数变量的增多,相应的卡诺图的复杂程度也成倍地增加。所以,卡诺图一般只适用于5个变量以内的情况。图2.6.1二变量到五变量最小项卡诺图
在逻辑函数的真值表中,输入变量的每一种组合都和一个最小项对应,这种真值表称为最小项真值表。将逻辑函数真值表中的最小项排列成矩阵,并且矩阵的横向和纵向的逻辑变量的取值按照格雷码的顺序排列(即相邻的数码只有一位码不同),这样构成的图形称为卡诺图。
由于相邻的最小项只有一个变量不同而其余变量都相同,如ABC和A′BC,ABCD和AB′CD。相邻最小项可以利用公式A+A′=1来消去一个变量,如ABC+A′BC=BC,ABCD+AB′CD=ACD。逻辑函数的化简实质上就是相邻最小项的合并。
卡诺图的排列特点就是具有很强的相邻性。
首先是直观相邻性,只要小方格在几何位置上相邻(不管上下左右),它代表的最小项在逻辑上一定是相邻的。
其次是对边相邻性,即与中心轴对称的左右两边和上下两边的小方格也具有相邻性。所以,四角的最小项也都是相邻的。凡是两个相邻的最小项,它们在图中也是相邻的。所以,二变量的最小项有2个最小项与之相邻,三变量的最小项有3个最小项与之相邻,四变量的最小项有4个最小项与之相邻,五变量的最小项有5个最小项与之相邻,以此类推。(https://www.xing528.com)
从图2.6.1可以看出,随着逻辑函数变量的增多,相应的卡诺图的复杂程度也成倍地增加。所以,卡诺图一般只适用于5个变量以内的情况。
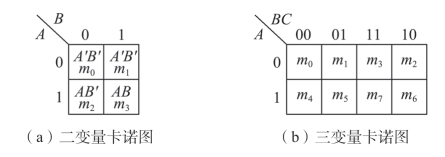

图2.6.1 二变量到五变量最小项卡诺图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




