【摘要】:为了方便化简逻辑函数的工作,运用基本公式导出了几个常用的公式,如表2.3.3所示。表2.3.3若干常用公式式A+A′B=A+B证明:A+A′B=(A+B)=1(A+B)=A+B上式说明,两个乘积项相加时,如果一项取反后是另一项的因子,则此因子是多余的,可以消去。式A′=AB′证明:A′′=A′=A′A′+A′B′=A′=A′上式说明,当A′和一个乘积项的非相乘,且A为乘积项的因子时,其结果就等于A′。当然,还可以推导出更多的常用公式。
为了方便化简逻辑函数的工作,运用基本公式导出了几个常用的公式,如表2.3.3所示。
现在将表2.3.3中的各式证明如下。
式(21)A+AB=A
证明:A+AB=A(1+B)=A·1=A
上式说明,在两个乘积项相加时,若其中一项以另一项为因子,则该项是多余的,可以删去。
表2.3.3 若干常用公式

式(22)A+A′B=A+B
证明:A+A′B=(A+A′)(A+B)=1(A+B)=A+B
上式说明,两个乘积项相加时,如果一项取反后是另一项的因子,则此因子是多余的,可以消去。
式(23)AB+AB′=A
证明:AB+AB′=A(B+B′)=A·1=A(https://www.xing528.com)
上式说明,当两个乘积项相加时,若它们分别包含B和B′两个因子而其他因子相同,则两项定能合并,且可以将B和B′两个因子消去。
式(24)A(A+B)=A
证明:A(A+B)=AA+AB=A+AB=A(1+B)=A·1=A
上式说明,变量A和包含A的和相乘时,其结果等于A,即可以将和消掉。
式(25)AB+A′C+BC=AB+A′C
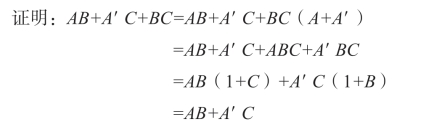
上式说明,当A和一个乘积项的非相乘,且A为乘积项的因子时,则A这个因子可以消去。
式(26)A(AB)′=AB′
证明:A′(AB)′=A′(A′+B′)=A′A′+A′B′=A′(1+B′)=A′
上式说明,当A′和一个乘积项的非相乘,且A为乘积项的因子时,其结果就等于A′。
从以上的证明可以看到,这些公式都是从基本公式导出的结果。当然,还可以推导出更多的常用公式。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




