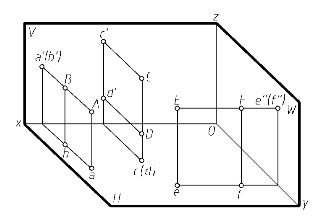
图2-12 重影点投影的直观图
从图2-12中可以看出,当空间两点位于垂直于某投影面的同一条投影线上时,两点在该投影面上的投影重合,则两点称为该投影面的重影点。如A点和B点称为V面上的重影点;C点和D点称为H面上的重影点;E点和F点称为W面上的重影点。显然,重影点必有两对同名坐标值相同,而另一对坐标值不等。如A、B两点的X、Z值相同,Y值不等;C、D两点的X、Y值相同,Z值不等;E、F两点的Y、Z值相同,X值不等。
判断重影点的投影的可见性由两重影点的不重合投影的相对位置来判断,或直接根据两重影点的第三坐标(坐标值不相等的那对坐标)的大小来判断。
例如,判断V面的重影点A、B在V面上的投影的可见性时,要从前向后观察,由H面投影可看出A点在前,B点在后,则在V面上,A点投影遮住了B点投影,所以前面的A点在V面上的投影可见,B点在V面上的投影不可见。也可以直接通过A点和B点的第三坐标值大小直接判断可见性,坐标值大者在相应投影面上的投影为可见,小者为不可见。比如,A点的Y坐标值比B点的Y坐标值大,所以A点在V面上的投影可见,B点在V面上的投影不可见。对于不可见点的投影用加圆括号的方式表示,如图2-13所示。
[例2-3]已知空间点A(30,20,40)、B(30、20、20),点C在点A的左方10、前方10、上方10,点D在点B的正左方10,求作点A、B、C、D的三面投影。
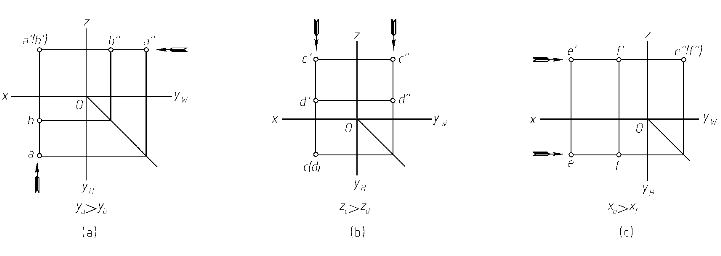
图2-13 重影点的投影(https://www.xing528.com)
作图步骤分析:
(1)A、B两点的投影可以根据点的投影与直角坐标之间的关系以及点的投影规律直接作出。
(2)从投影图所反映的点的位置关系可知,不同点X坐标的大小可反映它们的左右相对位置;Y坐标的大小可知它们的前后相对位置;Z坐标的大小则反映出两点的上下相对位置。所以作C点的三面投影时,可根据其与A点的相对坐标以及相对方位关系,在A点的投影基础上作出C点的三面投影。
(3)作D点的三面投影时可根据D点与B点的相对位置关系作出。
作图结果如图2-14所示。从作图结果可知,A点和B点为H面的重影点;B点和D点为W面的重影点;其可见性如图2-14所示。

图2-14 作A、B、C、D点的三面投影
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




