正圆柱螺旋面展开方法评估

问：正圆柱螺旋面适用的展开方法有哪些？

答：正圆柱螺旋面适用的展开方法有三角形法和简便展开法等。

1）三角形法展开。展开时将正圆柱螺旋面分成若干小三角形，然后求出各个三角形的实形，依次排列画出，得展开图。作图步骤如下：

①将一个导程内的螺旋面分成12等份（即将主视图中的导程和俯视图的圆作12等分），如图1-1a所示。每一部分曲面1—1₁—2₁—2可近似地看作一个空间的四边形，连接四边形的任一对角线，将四边形分成两个三角形。

②运用直角三角形法求实长，如图1-1a所示。将主视图四边形的下边线延长，过延长线作一直角，并将四边形各边投影高移至直角边上，在另一直角边上量取四边形在俯视图上的投影长度，则连接的斜边为实长。

③用所求得的实长，作出四边形1—1₁—2₁—2的展开图，在作其余各四边形时，可将1—1₁和2₁—2线延长交于O，以O为圆心、以O1和O11为半径分别作大小两圆弧，在大圆弧上量取11份弧长，得一个导程螺旋面的展开图，如图1-1b所示。

2）简便展开法。当正圆柱螺旋面的导程h和内径d、外径D已知时，可运用简便展开法作其展开图。作图步骤如下：

①作一直角，垂直边上量取h/2，水平边上量取πD/2、πd/2，连接斜边得半程大、小螺旋线的展开长度L/2、l/2，如图1-1c所示。

②作AB=L/2，过B点作BD⊥AB，并使BD=（D-d）/2=b。过D点作CD∥AB，并使CD=L/2。连接AC并延长使之与BD的延长线交于O点。

(www.xing528.com)

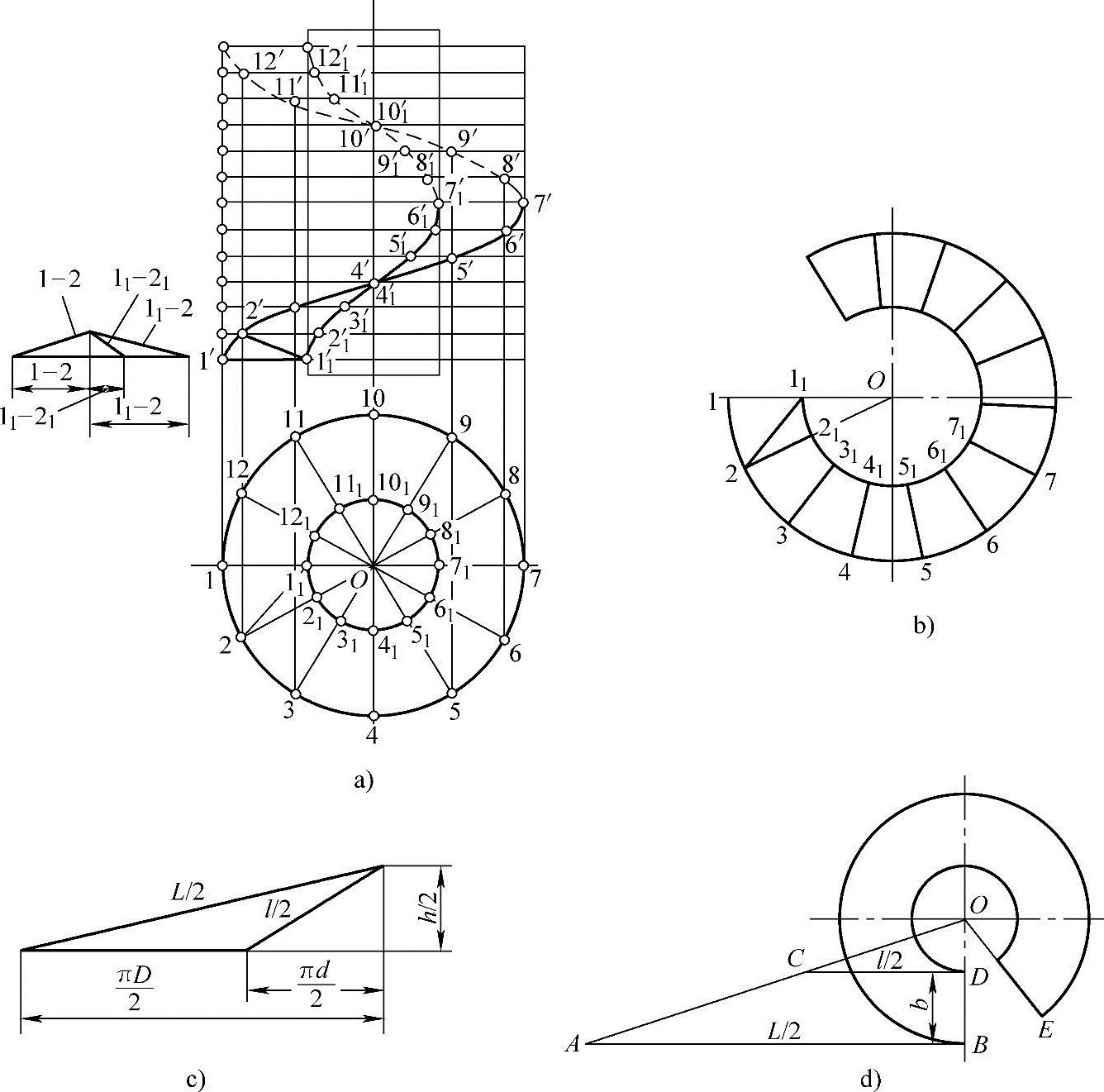
图1-1 正圆柱螺旋面的展开

a）三角形法求实长 b）三角形法展开图 c）半程螺旋线展开长度 d）简便展开法展开图

③以O点为圆心、分别以OD、OB为半径作圆弧，在圆弧上量取2倍于大螺旋线的展开长度L/2得E点，连接oe与小圆弧相交，得正圆柱螺旋面的展开图，如图1-1d所示。

试题选解：

正圆柱螺旋面的近似展开的方法一般有（ ）。

（A）放射线法 （B）简便展开法

（C）旋转法或三角形法 （D）简便展开法或三角形法

解：正圆柱螺旋面适用的展开方法有三角形法、简便展开法等，故答案D是正确的。所以正确答案应选D。