AHP法群组评判的实用技巧

作为一种科学有效的决策分析工具，AHP 方法已经受到了越来越广泛的重视和应用。然而，正如一切其他工具一样，AHP 的有效性往往和工具使用者在实际应用时所使用的实用技巧有很大的关系。此处介绍AHP 方法在群组评判中的实用技巧及注意事项。

在运用AHP 方法进行决策分析时，评判者往往不是一个人，而是若干人。尤其是对重大问题的决策分析，评判者有时甚至是一个庞大的专家团。这时就会遇到群组评判的问题。目前，在AHP 决策分析的群组判断中，人们常用评分算术平均法、评分几何平均法与权重算术平均法等三种方法。

1.评分算术平均法

设某评判者k 对某项指标的n 个下层同类对象评判的判断矩阵为：

其中　

如果评判者有m 名，则会得到m 个判断矩阵。平分算术平均法就是将各评判者对各元素的评分取算术平均值：

然后将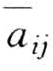组成新的判断矩阵如下：

采用评分算术平均法综合以上群组评判结果，可得新的判断矩阵及各项成果权重排序。这一方法在算法上比较简单，但它在理论上存在着很大的缺陷。它不能保证判断矩阵的互反性。其使用往往会破坏判断矩阵的相容性和整体性。从相应的CI、CR可以看出其一致性很差。

2.评分几何平均法

评分几何平均法是近年来AHP 研究的一个重要课题。此方法有较强的实用性。

评分几何平均法是对各判断矩阵的元素进行几何平均，其形式如下：

其中m 为评判者人数。由此可得到以下新的判断矩阵：

由上述矩阵可得到新的权重。

评分几何平均法在算法上保持了评分算术平均法的简便性，它可以省掉对各专家评出的判断矩阵的一致性检验。只要对经过评分几何平均的判断矩阵进行一次一致性检验便可。从形式上看，评分几何平均法与评分算术平均法有相似之处，它们都是首先对各判断矩阵的元素进行处理并汇拢成一份新的判断矩阵表，然后再计算新判断矩阵的特征向量，即评价对象的权重，所不同之处只是汇总处理方法不一样。但理论研究表明，评分几何平均法，能保证判断矩阵的互反性，其准确性与科学性较评分算术平均法要高很多，所以评分几何平均法在目前是比较受到重视的一种AHP 群组决策的新方法。(www.xing528.com)

3.权重算术平均法

权重算术平均法是迄今为止被运用得最为普遍的一种AHP群组决策分析方法。其特点是分而合之。首先让评判人员分别对测评对象进行评判，再分别算出各自的评判结果，即测评对象的权重及判断矩阵的一致性程度。凡是通过一致性检验的判断矩阵为有效评判，否则为无效判断，需要进行修改或剔除。最后对这些由不同评判人员评出的有效判断的权重取算术平均。设第k个评判人员对第i 项评判对象的有效判断权重为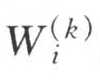，则m 名评判人员对该对象的有效判断权重平均值为

此方法的最大优点是可以对各位专家的评判结果分别进行检验，对不符合逻辑一致性的判断矩阵能及时进行修改或剔除，从而能够较有效地保证总体综合分析的可信度和可靠性。从理论上讲，其综合手段不会破坏各判断矩阵的相容性。所以，权重算术平均法在目前来说，是一种较为可靠而且运用最多的群组决策方法。

4.多层次结构的权重算术平均法

对多层次的系统运用权重算术平均法主要有两种途径：

（1）对各评判人员的各直接判断矩阵权重取算术平均，然后再由下向上计算综合权重。

（2）对各评判人员的综合判断矩阵权重直接取算术平均。

可以通过实例证明这两种方法的最终评判结果是相同的，仅权重的相对值略有不同。然而，第二种方法要比第一种方法简便得多。所以在一般情况下，第二种方法被运用得更为普遍。

5.评分几何平均法与权重算术平均法计算结果的差异

目前，评分几何平均法与权重算术平均法是两种用得较多的群组评判方法，它们在使用中各有利弊。在城乡建设与环境保护部1987年下达的科研项目——劳动负荷综合测评模型中，研究人员对此进行过实验与讨论。他们对影响劳动负荷的主要因素分成三大类：体力因素、环境因素与心理因素。每一大类因素下还有很多相关的子因素，这里就不详细叙述了。他们首先要求测评对象根据层次分析法进行二二比较判断分析，并得到了大量的判断矩阵表。

为了验证部分几何平均法与权重算术平均法对同层次结构及同评测对象的计算结果的差异，他们抽取了4 批样本（每批抽5张调查表）。对每批样本分别采用上述两种方法处理，从而得到了2套对同一评判对象三大因素的权重、W以及有关的一致性检验指标CR。根据以上数据，可得到以下一些初步的结论：

（1）当极大多数的评价具有较好的一致性时，用评分几何平均法、权重算术平均法得到的特征向量的各分量最大误差小于5% ，用评分几何平均法汇总得到的一致性也是令人满意的。

（2）当半数以上评判人员的评价不具有较满意的一致性时，用评分几何平均法汇总得到的一致性也较差。但若不把“不一致”的评判表剔除掉，两者得到的特征向量分量的最大相对误差在10%以下，相差不算太大。