在工程技术领域,有些问题是可以量化的,而有些问题与社会经济系统的某些决策问题一样,是难于对系统进行量化的。但这些被测量对象的属性大多数具有相对性质,系统中各因素相关度的测量可通过人的判断和经验来完成。AHP 方法就是根据这些系统中元素测度的特点提出了相对重要性的比例标度。两个元素相对重要性的比较可变换为一个数。表5-6 说明了相对重要性的比例标度。
表5-6 相对重要性的比例标度

以下用一个拱式渡槽的结构安全性评定的例子说明相对重要性的比例标度和判断矩阵的建立的方法。
1.将结构分解(化整为零)
灌区建筑物老化病害的评定中都牵涉到结构安全性,现有一常用的拱式渡槽,根据其结构特点可将其分解(化整为零)为三个重要组成部分:拱上结构(槽身)、传力结构(主拱圈)和基础(墩台)。三者对渡槽结构安全性的影响程度分别用W1、W2和W3 表示。
2.确定比例标度
在作比较判断时,经常可以用一些问题来帮助获得一个相对标度。例如在比较元素A 和B 时,可以问:
你认为A 和B 中,哪一个更为重要,或哪一个有更大的影响?
或者,A和B比较起来,你更愿意发生哪一个?
A和B比较起来,你更喜欢哪一个?
例如,影响拱式渡槽结构安全性的各影响因素哪一个更为重要?可以得出较为一致的答案:基础最重要,传力结构次之,上部结构再次之(相对最不重要)。
但是,我们还需要更深一步知道“最重要”到底“最”到什么程度?次重要又“次”到什么程度?“最不重要”又“不重要”到什么程度?也就是要有一定的量化。这就是AHP方法提出的相对重要性的比例标度。
为使问题更清晰,用表5-7予以表达。
相对重要性的比例标度是由二二比较而得。
拱上结构与其自身之比: W1/W1=1
表5-7 渡槽主要组成部分对安全性的重要性比例标度表

拱上结构与传力结构之比:W1/W2=1/3
拱上结构与基础之比:W1/ W3 =1/5
同理可得表中其他各重要性的比例标度值。(https://www.xing528.com)
需要特别说明:
(1)上表中的重要性比例标度值应由渡槽专家给定,以确保其可靠性。
(2)在专家给比例标度值时,仅考虑“二二”比较,不要掺入第三个元素,这一点也很重要。因为在人们判断的思维过程中,前后的判断有出入是正常的,不一定是前者不当,不要用后者去修改前者,当然,也不要用前者修改后者。否则会影响判断的准确性。如上表中,W1/W2=1/3,W2/W3=1/3,就不要由此而去把W1/W3=1/5再修改为1/9。因为前者W1/W2的相对重要性比例标度的理想值可能不是3,而是1/2.5或2.6…,仅是用最接近理想值的这一整数3所表示,而后者W2/W3的理想值可能也是如此。若硬将W1/W3改为1/9,反而可能离真值更远。前后的思维是否一致,后面还会做出专门的检验。
3.建立判断矩阵A
层次分析法的信息基础是判断矩阵。根据判断矩阵,利用排序方法,可以得到各方案相对重要性的排序。为了说明排序方法的原理,我们仍以上述渡槽为例。
上表的形式实际已给出了判断矩阵A 的所有元素:
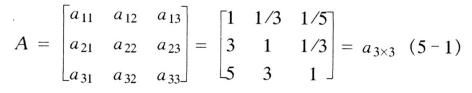
可用通用公式表示为:

显然,aij=1/aji,aii=1,i,j=1,2,n,此例中n=3。
4.用方根法计算判断矩阵的特征向量
由矩阵理论,用某一重量向量W=[W1,W2,…,Wn]T右乘A 矩阵得:
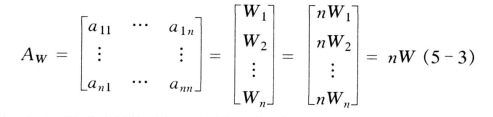
向量W称为判断矩阵A 的特征向量。层次分析法的基本计算问题是计算判断矩阵的最大特征根λmax和特征向量W。特征向量通用算法是幂乘法和方根法(也称几何平均法),此外还有规范列平均法(又称为和积法)。一般来说,计算矩阵的最大特征根及其相应的特征向量,并不需要追求很高的精度,因为判断矩阵本身已带有不少误差。方根法和规范列平均法与幂乘法相比,虽然比较粗糙,但只需手算或小型计算器即可,十分方便。
(1)计算判断矩阵行元素的乘积Mi
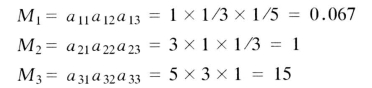
(2)计算Mi 的n 次方根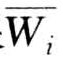
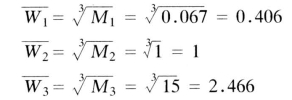
(3)对向量![]() =[0.406,1,2.466]归一化
=[0.406,1,2.466]归一化
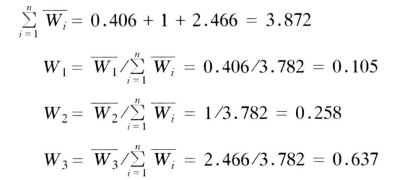
W=[0.105,0.258,0.637]T 即为所求的特征向量,若其满足一致性,就是所求渡槽三个重要组成部分间的重要性相对比例标度,即后面所称谓的“权重”。这种排序方法也称为特征向量法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




