结构承载力安全性复核优化措施

一、结构计算方法概述

结构安全是其正常运行的保证。结构承载力的安全性是安全性复核的最主要内容。对承载力的计算方法，直至19 世纪，材料力学、弹性力学和材料试验科学得到了较大的发展，以及比较理想的弹性材料——钢材得到了广泛的应用，对结构设计理论起到了很大的促进作用，基于弹性理论的容许应力法才得于问世，并迅速而广泛应用于结构设计中。

结构承载力的计算方法，经历了容许应力法、破损阶段法、极限状态法和近似概率法等方法的不断完善与发展的过程。

1.容许应力法

容许应力法要求结构构件在使用期间，由一般材料力学法求得截面上任何一点的应力σ应满足下式的要求：

式中：［σ］为结构材料的某一允许应力值；f 为结构材料性能，其值由试验确定；K 为安全系数，由经验确定。

容许应力法是一种传统的设计方法，一些国家仍沿用至今。它的主要优点是应用简便。对各种结构的设计，一般认为可以满足使用要求，只要保持在使用荷载下的低应力，混凝土梁的扰度、裂缝宽度等很少会达到临界值（对高强度混凝土和钢筋、预应力混凝土构件则必须进行正常使用性能的验算）。容许应力法的主要缺点是仅由一个笼统的按经验所确定的安全系数来保证，缺乏明确的结构可靠度概念；所给的一系列容许应力并不能保证各种结构具有一致的可靠度水准；当一个荷载抵消其他荷载的效应时，容许应力模式可能不安全，特别是一个相对可预估的恒载效应抵消一个像风荷载那样可变性很大的荷载效应时，尤为严重。

如图4-54（a）所示的混凝土结构，用容许应力法计算时，其材料的容许抗拉和抗压强度分别为1.4MPa和12.6MPa。结构分别在恒载、风载作用下的应力及叠加后的应力见图4-54（b）。此时底部截面最大拉、压应力仅为相应容许应力的50%。但只要风载增加20%［应力计算见图4-54（c）］，就能使底部截面A 点的拉应力达到抗拉强度的容许值。这就是许多结构破坏的原因。

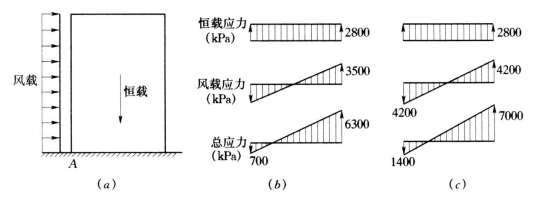
图4-54　允许应力法计算悬臂梁应力

（a）受风荷载作用的悬臂梁；（b）设计荷载下梁底面应力；（c）风荷载增加20 %的梁底面应力

2.破损阶段法

上世纪20年代初国外已提出了受弯构件考虑塑性变形的计算方法，后来发展为破损阶段法。用破损阶段法对构件的强度进行计算时，假定钢筋和受压混凝土均已达到塑性状态，以截面所能抵抗的破损内力为依据建立计算公式。

如受弯构件，其一般表达式为

式中：M 为标准（使用）荷载作用下的截面弯矩；Mp 为截面破损时的抵抗弯矩；K 为构件强度总安全系数。

破损阶段法的主要优点是考虑了结构构件材料的塑性性能，反映了构件截面的实际工作情况，所以计算结果比较准确，且一般较按容许应力法的计算结果为经济；其主要缺点仍是采用了笼统的总安全系数，用以估计使用荷载的超载和结构材料性能的离散性，而缺乏明确的可靠度概念。

3.极限状态法

在破损阶段法的基础上，前苏联学者早在1950年前后就提出了结构极限状态的概念和计算方法，1955年前苏联就正式颁布了按极限状态设计方法的各种设计标准及规范，其中包括《混凝土及钢筋混凝土结构设计标准及技术规范》，该规范中的一般设计表达式为

式中：ni 为过（超）载系数；为标准荷载产生的内力；φ为函数；m、mg分别为结构构件及钢筋的工作条件系数；kh、kg分别为混凝土及钢筋的匀质系数；、分别为混凝土及钢筋的标准强度；S 为截面的几何特征。

我国也曾应用前苏联的这一规范，并依据这一计算方法于1966年制定了BJG21—66《钢筋混凝土结构设计规范》。此后，根据我国自己的研究成果和工程经验，又于1974年前后颁布了一套以多系数分析单系数表达的极限状态设计方法的工业与民用建筑结构设计规范。此外，SDJ20—78《水工钢筋混凝土结构设计规范》及JTJ200—82《港口工程技术规范·混凝土和钢筋混凝土（设计部分）》也都采用了这种设计方法，仅在安全系数的取值略有差别。

极限状态设计方法是结构设计的重大发展。这种方法明确地提出了结构极限状态的概念，不仅规定了结构设计的承载能力、变形及裂缝出现和开展三种极限状态，而且放弃了前两种方法所采用的单一、笼统的安全系数，采用了超载、匀质和工作条件三个系数，以分别考虑荷载、材料性能和工作条件等方面随机因素的影响。在标准荷载和材料标准强度取值方面，开始采用了数理统计手段分析确定其相应的系数。此法较全面地考虑了结构的不同工作状态，比前两种方法要客观得多，比较符号客观实际。但是，极限状态计算方法仍然没有给出结构可靠度的定义和分析可靠度的方法，此外，对于保证率的确定、系数的取值等方面仍然带有不少主观经验的成分。

例如，原规范SDJ20—78 的设计原则是“多系数分析、单一安全系数表达的极限状态设计法”。其设计原则及存在问题可由以下简支结构加以说明。

承受自重gk（永久荷载）和集中活载Qk（可变荷载）的单筋矩形截面简支梁，跨中正截面受弯承载力（图4-55）设计表达式为

其中

式中：K 为截面的强度安全系数，M 为由荷载标准值gk、Qk作用下的截面内力，Mp为截面极限破坏内力，上式符号仍沿用原规范的老符号。

图4-55　简支梁跨中正截面承载力设计

在SDJ20—78规范的表达式中，虽然有部分参数（主要是材料设计强度）也是由统计分析得来的，但其他参数都是作为定值看待的。而作为衡量构件安全度的指标——安全系数K，则至少有3个问题：①在不同性质的荷载作用下，K 均取用同一值，显然这是十分笼统和不够合理的，因为不同的荷载，其变异性是完全不同的，对结构安全的影响程度也完全不同。②K 是完全由工程经验确定的，它的取值缺乏足够的科学根据。③K并不能准确地反映构件的安全度，如该规范规定，钢筋混凝土构件受弯时的K 取用为1.50，而斜截面受剪时的K 取用为1.60，但不能因此认为受剪时的实际安全度比受弯时高。

所以，单一安全系数K 并不是一个好的衡量安全度的指标。

综上所述，虽然结构设计的方法在不断地完善，甚至确定设计参数时已部分应用了数理统计方法，但它们仍然没有脱离以经验为主来估计结构可靠度的范畴。这些方法使人们常常误认为，只要设计中采用了某一规定的安全系数，结构就是100% 的可靠，亦即将安全系数与结构可靠度简单地等同起来。实际上，这些规定的安全系数是人们对许多未知的或难以了解和控制的因素的估计，以及对可靠度的期望而经验地加以确定的。

4.概率法——概率极限状态法

前苏联学者在可靠度方面的研究取得的成果最早。早在1947年尔然尼采就提出了一次二阶矩理论的基本概念，1954年提出了可靠指标的基本公式，但未加以发展并应用于实际。1970年以来，对于结构可靠度方面的研究相当活跃，世界上许多国家都取得了非常有价值、能直接用于工程设计的应用性成果。在工程结构设计方法上，已形成了以概率及数理统计理论为基础的极限状态设计方法，简称“概率设计法”。根据概率设计法的发展阶段和精确程度，目前可将其分为三个水准：

水准Ⅰ——半概率法。对荷载效应和结构抗力的基本变量部分地进行数理统计分析，参照工程经验引入某些经验系数。故又称为半概率半经验极限状态设计方法。

水准Ⅱ——近似概率法。对结构可靠度赋予了概率定义，以结构的失效概率或可靠指标来度量结构的可靠性，并建立了结构可靠度与结构极限状态方程之间的数学关系。在计算可靠指标时考虑了基本变量的概率分布类型和采用了线性化的近似手段，在截面计算时一般采用分项系数的实用设计表达式。当前，近似概率法已进入了实用阶段，成为许多国家制订标准规范的基础。

水准Ⅲ——全概率法。对结构各种基本变量分别采用随机变量或随机过程描述，要求对整个结构采用精确的概率分析，求得结构最优失效概率作为可靠度的直接度量。但因目前对结构基本变量的客观统计规律掌握不足，不论在理论上还是在实际应用上都还存在一定的困难，所以目前仍处于研究阶段。

二、可靠度设计的基本概念

（一）随机变量

大量实践证明，影响结构可靠性的各种参数，如荷载、材料强度和几何尺寸等都不是定值，均存在不同程度的不确定性和变异性，从概率的观点看，这种不确定性和变异性称为随机性，变量则称为随机变量。随机变量的特征为，每次都以不确定的值出现，但也不是完全无规律的，经多次观测可统计出它出现的规律，即对应于每一个可取的值，都有它确定的出现概率。为了工程的安全和经济，在结构设计中引入概率统计理论的观点和方法来处理这种随机性是十分自然和必要的。

在结构可靠度分析中，常用随机变量的概率分布有正态分布、对数正态分布和极值I 型分布。若用X 表示随机变量，相应有关的概率分布函数F（x）、密度函数f（x）、均值E（X）、方差D（X）的计算公式如下。

1.正态分布

式中：μ、σ分别为X的均值、标准差。

2.对数正态分布

式中：μ、σ分别为lnX的均值、标准差。

3.极值Ⅰ型分布

由上式知，f（x）及F（x）主要由随机变量x 的两个统计参数μ（均值）和σ（标准差）确定。μ和σ均可由大量的统计资料用数理统计方法求得。Vx 为x 的变异系数。

对于随时间变化的可变作用，则应采用随机过程的概率模型。由于目前对各类作用随机过程的样本函数（即实现）及其性质了解不多，为了简化分析，可以将各类可变作用按平稳的随机过程来考虑，如常用的作用随机过程有平稳二项随机过程、泊松随机过程和平稳正态随机过程。

因GB50199—94《水利水电工程结构可靠度设计统一标准》（以下简称《水工统标》所采用的结构可靠度分析方法为一次二阶矩法（后文将介绍），该方法要求各种基本变量都是按随机变量模型来考虑的，故须将上述可变作用随机过程转化为是随机变量的设计基准期最大作用。若可变作用随机过程为Q（t），设计基准期最大作用为QT，显然QT = maxQ（t），其中0 ≤t ≤T。

风压力、雪压力及静水压力等无法人为控制的可变作用，在设计基准期内最大值QT 的概率分布FT（x）可用极值统计方法确定。极值统计法进行数理统计分析的具体步骤如下。

（1）将设计基准期等分为n 个时段，τ= T/n。时段τ的选择，宜使每个时段的作用最大值Qi 相互独立。

（2）每个时段τ内选一个作用最大值Qi，并对Qi 进行调查统计，取得Qi 的数据样本。

（3）对Qi 的样本进行统计分析，计算统计参数估计值，作出样本的频数直方图，估计概率分布模型，并经概率分布模型的优度拟合检验，选定时段τ内的作用最大值概率分布函数Fτ（x）。

（4）根据时段概率分布Fτ（x），按式（4-174）计算设计基准期T 内作用最大值QT 的概率分布FT（x）为

（5）由概率分布FT（x）推求设计基准期内作用最大值QT的统计参数——均值μT 和标准差σT。

经过推导不难发现，当Fτ（x）符合极值Ⅰ型分布时，FT（x）也符合极值I 型分布，其统计参数为

式中：μτ、στ分别为Qi 的均值和标准差。

（二）可靠度设计方法的模型

随着对结构可靠性研究的进一步深入，已提出的定量计算可靠度的方法可归结为数学模型法和物理原因法两大类。

数学模型法是设想可靠性的变化遵从某些由实验确定的统计规律的方法。这类方法发展为两种：一种是把可靠性看作时间范畴的量，即可靠性随时间的延续按某一确定的规律变化；另一个是把可靠性视为某些偶然因素的结果，失效是由于某些偶然因素的出现引起的，因而可靠度作为随机事件发生的概率来计算，它多用于瞬时一次使用的结构。数学模型法的缺点是没有阐明失效产生的原因，也没有指出消除失效的可能性。目前这种方法在电子和机电系统应用较为广泛。

物理原因法也分两种。其一是应力—强度模型法，或称荷载效应—结构抗力模型法。这种方法认为施加于结构上的应力和结构的强度均为随机变量，并服从一定的分布。结构的可靠度是结构强度大于施加于结构上应力的概率。结构可靠度计算所用的荷载、材料强度和几何参数等特征量均由大量资料统计获得，并不是结构可靠性本身的特征量。这一方法考虑了导致结构失效的原因，且经过许多学者的不懈努力，逐渐发展并完善了动态模型，使它变成了结构可靠性分析计算中广泛应用的基本模型。其二是把可靠度定义为随机过程或随机场不超出规定任务水平的概率。此法引入了系统空间及系统状态允许域，当系统随时间变化的轨迹超出了系统空间或状态允许域则认为系统失效。此法同样需要一定的初始统计资料才能导出随机过程或随机场的参数，但这种参数的获得要困难得多。

根据结构的实际情况进行分析，近似概率法对具体结构进行可靠度计算时，最为合理的计算方法是应力—强度模型法。

应力——对结构功能有影响的各种外界因素的总称，也称为作用或荷载效应。如力、力矩、温度、振动、腐蚀等因素，这些因素倾向于使结构产生破坏。如荷载使结构产生的内力和变形，如轴力、弯矩、剪力、扭矩、挠度位移和裂缝等。

强度——结构承受应力的能力，也称为抗力。主要取决于结构材料的强度、截面尺寸及计算模式等。

应力和强度的概念，是力学中相应概念的延伸。在分析计算中，力学中所定义的应力依然适用，应用时，只要应力与强度的单位保持一致即可。

结构可靠度是结构强度大于施加于其上面应力的概率，或者说，当施加于结构上的应力大于结构强度时，结构失效。

在进行结构可靠性分析中作出如下基本假设：

（1）结构强度为一非负随机变量或随机过程，用R 或R（t）表示；

（2）应力为一非负随机变量或随机过程，用S 或S（t）表示；

（3）当应力不超过结构强度（S ≤R）时，结构被认为是可靠的；否则，S＞R 时，被认为是结构失效（故障或破坏）；

（4）结构失效仅由于应力作用而发生；

（5）计算应力和强度的一切力学公式仍然适用，但公式中的确定量均视为随机变量或随机过程。

应力和强度本身存在着客观不确定性、离散性，以及随时间变化的不确定性，用概率统计的方法计算结构的可靠度或失效概率是最为有效的方法。根据应力和强度的特性，应力—强度的可靠性计算模型可归结为三种基本形式：

（1）应力—强度随机变量模型。其中，应力S 和强度R 均为随机变量。

（2）应力—强度半随机过程模型。其中，应力S 和强度R之一为随机过程，而另一个为随机变量。

（3）应力—强度全随机过程模型。其中，应力和强度均以随机过程概型来描述。

通常，把应力—强度随机变量模型称为静态模型。它忽略了时间因素，认为应力和强度不随时间变化，或者认为具有瞬态性质的一次作用。这种模型在理论上较为成熟。半随机过程模型和全随机过程模型均称为动态模型，这种考虑到时间因素的模型是静态模型的一种扩展，在可靠性数量特征的描述与分析计算上，要比静态模型复杂得多，由于目前对各类作用随机过程的样本函数及其性质了解不多，所以结构可靠性的动态模型还处于研究阶段。

（三）极限状态

结构或结构的一部分超过某一特定状态就不能满足设计规定的某一功能要求，此特定状态则称为该功能的极限状态。也是区分结构工作状态是可靠或失效的界限。

根据功能要求，国际上通常把极限状态分为承载能力和正常使用两类。

1.承载能力极限状态

对应于结构或结构构件达到最大承载能力，或达到不适于继续承载的变形的状态称为结构的承载能力极限状态。当结构或结构构件出现下列状态之一时，即认为达到或超过了承载能力极限状态。

（1）结构发生滑移、上浮或倾覆等不稳定情况；

（2）整个结构或结构的一部分转变为机动体系而丧失承载能力；

（3）整个结构或结构的一部分丧失弹性稳定（如压屈等）；

（4）构件截面因强度不足而发生破坏（包括疲劳破坏），或因过度塑性变形而不适于继续承载；

（5）土、石结构或地基、围岩产生深透失稳（变形）等。

2.正常使用极限状态

对应于结构或构件达到影响正常使用或耐久性能的某项规定限值的状态称为结构的正常使用极限状态。当结构或结构构件出现下列状态之一时，即认为超过了正常使用极限状态。

（1）影响结构正常使用或外观的变形；

（2）影响正常使用的过大振动。结构裂缝或局部损坏，对外形、耐久性以及防渗结构抗渗能力等有不良影响或产生人们心理上不能接受的感觉。

（四）结构的可靠度与失效概率

结构可靠度的定义已在前面述及。结构在达到承载能力的极限状态和正常使用的极限状态之前，结构处于正常运用状况，称结构为可靠。当结构达到和超出任一状态时，则结构处于失效状态。结构的极限状态可用极限状态函数（或称功能函数）来描述。设有n 个相互独立的随机变量Xi（i=1，2，…，n）影响结构的可靠度，n 个随机变量主要为作用于结构的各种荷载、结构材料的各种有关性能和结构的几何尺寸等，结构的功能函数可表示为

功能函数也可由结构构件的荷载效应S 和结构抗力R 两个随机变量来表达

因为各种荷载、结构材料的各种有关性能和结构的几何尺寸等均为随机变量，所以式中R 和S 为随机变量，进而功能函数Z 也是随机变量。

显然：当Z = g（R，S）= R - S ＞0时，结构可靠；

当Z = g（R，S）= R - S ＜0时，结构失效；

当Z = g（R，S）= R - S = 0时，结构处于极限状态。

由于影响结构可靠性的各主要因素存在不确定性，所以，从概率论的观点来研究结构的可靠性，绝对可靠是不可能的，绝对可靠的结构也是不存在的。但综合考虑结构所具有的风险和经济效果，只要失效概率小到人们可以接受的程度，就可认为该结构是可靠的。从极限状态方程可以看出，无论结构设计者采用怎样保守的设计方案，也总还可能出现某一或一些基本变量X1，X2，…，Xn的组合，例如荷载遭遇高值，而材料强度又出现低值，使得功能函数Z＜0，亦即结构失效。所以，失效是指结构或结构的一部分不能满足设计所规定的某一功能（如承载能力或正常使用等）要求，即达到或超过了某一功能极限状态的极限。这表明在实际工程设计中，任何一种设计方案所对应的结构，其在规定条件下和规定时间内完成规定功能这一“事件”，既不是必然事件，也不是不可能事件，而是一个随机事件。失效概率即指结构构件处于失效状态下的概率。

根据定义，描述结构可靠性大小的可靠度——结构能够完成规定功能的概率ps 可表示为

因事件｛Z ≥0｝与事件Z＜0互逆，结构的失效概率——结构不能完成预定功能的概率pf 则为

上式表明失效概率pf 与可靠概率ps具有互补关系，因而，失效概率pf 也能用来度量结构的可靠性。显然，pf 大，可靠性小；pf 小，可靠性大。

如果已知极限状态方程（4 - 177）中基本变量X1，X2，…，Xn的联合分布密度函数为fx1，x2，…，xn（x1，x2，…，xn），则结构的失效概率pf 为

（五）可靠指标

计算失效概率pf 最理想的方法是由式（4-181）精确求解，但除少数情况（如极限状态方程为线性、且基本变量均正态分布等）外，通过上式多重积分直接求pf 是十分复杂的，不仅计算工作量非常大，有时甚至难于获得解答。为此，在实用上就发展了近似概率法。

近似概率法的主要特点是：①把随机变量看成仅由均值μ（一阶矩）及标准差σ（二阶矩）2个统计参数来表征，而不考虑二阶矩以上的统计特征值；②在运算过程中，对非线性的功能函数作泰勒级数展开时，仅取一次项作为其近似表达式，即线性化；③研究并引入了另一个衡量结构可靠性的数量指标——可靠指标β，使计算的大为方便。

现利用式（4-181）来讨论一种最简单情况的失效概率pf的计算。

1.正态分布

由结构的功能函数Z=（R，S）的定义知，R 和S 分别为结构抗力与荷载效应，当R、S 相互独立且均为正态分布时，则Z=R-S 也属正态分布。若μR，μS 为R、S 的均值，，为R、S的方差，则Z的均值μZ、方差和概率密度函数fZ（z）分别为

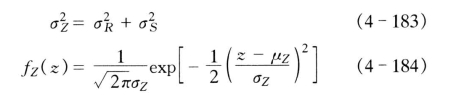
图4-56　Z=R—S 的概率分布及β、pf的关系

图4-56表示随机变量Z的分布，Z＜0的概率为结构的失效概率，即pf =P（Z＜0），此值等于图4-56中阴影部分面积

式中　φ（·）为标准正态分布函数。

由上式可以看出，β与pf 之间存在一一对应的关系（具体数据见表4-44）。

表4-44　可靠指标β与可靠概率ps、失效概率pf

将式（4-182）、式（4-183）代入式（4-186）得

则

由图4-56知，失效概率pf 是概率密度函数fz（z）的尾部与OZ 轴所围成的阴影部分面积，而可靠指标β值也能反映这一面积的大小。很明显，β越大，pf 就越小，即结构越可靠，所以β称为“可靠指标”。因此，β和pf一样，也可用以度量结构的可靠性。

由于β的值是由功能函数Z 的一阶原点矩μZ 和二阶中心矩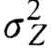确定的，因此，以β为可靠指标的设计理论称为一次二阶矩模式，或称近似概率模式。

2.对数正态分布

因为抗力和荷载效应大多趋向于偏态分布，按正态分布计算时将产生较大的误差。因此有的学者建议假定R 和S 服从对数正态分布。即R 和S 的对数lnR 和InS 服从正态分布。lnR 和LnS 的平均值为μlnR、μlnS，标准差为σlnR、σlnS。此时，功能函数Z=lnR -lnS 也服从正态分布，其均值和标准差为μZ =μlnR -μlnS和由对数正态分布的性质可知

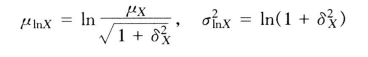
式中：δX 为变异系数，δX=σX/μX。

将上述二式代入式（4-188）得

当δR 和δS 小于0.3时，上式可以进一步简化， 取

其误差小于2%。且当δR、δS 很小或者近似相等时，则有

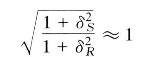
将上述结果代入式（4-189），可得简化的对数正态分布可靠指标β的计算公式为

（六）一次二阶矩方法

一次二阶矩方法是计算结构可靠度常用的一种简便、实用的近似方法。在结构可靠度的计算中，由于这一方法只利用了基本变量的一阶矩均值和二阶矩方差这两个统计参数，并对非线性的功能函数作泰勒级数展开时仅取一次项即线性项作为其近似表达式，故称为一次二阶矩方法。

一次二阶矩方法因功能函数的泰勒级数展开点的选择不同，可分为中心点法和验算点法两种。

1.中心点法

设基本变量X1，X2，…，Xn 为n 个相互独立的正态分布随机变量，当功能函数（即状态函数）Z 为线性函数时

其中，a0，a1，…，an 为已知常数，Z 的均值μZ 和方差分别为

其中：μi，σ（i=1，2，…，n）分别为Xi 的均值和方差。

类似于式（4-187）的推导，可得结构的失效概率pf 的表

其中：β为可靠指标达式

在一般情况下，结构的功能函数常为非线性函数，基本变量也可能不是正态分布。为了求得结构的可靠度，中心点法首先是将功能函数Z= g（X1，X2，…，Xn）在基本变量的中心点（即均值）μ1，μ2，…，μn处作泰勒级数展开，并取级数的一次项（即线性项）为Z 的近似式

式中Xi=（X1，X2，…，Xn），μi=（μ1，μ2，…，μn）。

然后由上式可得Z的近似均值和方差为

如果X1，X2，…，Xn 相互独立，则式（4-199）可简化为

求出μZ和σZ后，无论Xi（i=1，2，…，n）是否服从正态分布，中心点法均参照式（4-195）确定可靠指标β，即并认为结构失效概率仍可由pf=φ（-β）计算。

显然，当且仅当功能函数Z=g（X1，X2，…，X ）是正态随机变量X1，X2，…，Xn 的线性函数时，中心点法所得计算结果才是精确的。

中心点法的优点是：可以直接给出可靠指标与基本变量统计参数之间的关系，计算简便。缺点是：①一般仅适用于β=1～2的可靠度分析；②除少数情况（功能函数为线性，变量均正态分布）外，不能考虑基本变量的实际概率分布；③对于非线性功能函数，在中心点（均值点）处作泰勒级数展开，只取线性项，计算结果误差大，如当选择数学表达式不同但力学等效的非线性极限状态方程时，将给出不同的β值。例如对只有两个基本变量——抗力R、荷载效应S 的情况，我们可以列出两个极限状态等价但数学形式不同的功能函数

根据中心点法，相应于式（4-200）和式（4-201）得到的可靠指标β分别为

其中：μR、和μS、分别是R和S的均值与方差。比较式（4-202）和式（4-203），可看出两个β并不相等。其原因是将非线性功能函数在中心点线性化的结果。

2.验算点法

针对中心点法存在的问题，人们提出了验算点法——改进的一次二阶矩方法。这一方法因被国际结构安全联合委员会（JCSS）所采用，故也称为JC法。该法能在计算工作量增加不多的情况下：①能够考虑非正态分布的基本变量；②能对可靠指标β进行精度较高的近似计算；③还可以算出各基本变量的“设计验算点”，并由此导出分项安全系数，使概率设计方法与安全系数法联系起来，从而大大促进了可靠性理论的工程应用。

目前验算点法已被很多国家所采用，我国《建筑结构设计统一标准》、《水工统标》等均采用了这一计算方法。

为了说明β的几何意义，将一般正态分布随机变量Xi（i=1，2，…，n）作标准正态分布变换［18］，即令：

或

此时，（i=1，2，…，n）为标准正态变量（均值为0，标准差为1）。

把式（4-205）代入相应于式（4-191）的线性极限状态方程，可得该极限状态方程在新坐标系（标准正态坐标系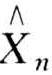）…中的表达式为

该方程在新坐标系中为一极限状态平面，它将构成的空间划分成可靠区与失效区两个部分，如图4-57所示（以两个变量为例）。

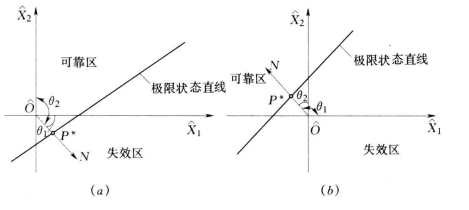
图4-57 可靠指标β的几何意义示意图

（a）当μZ≥0时：β=|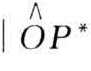|；（b）当μZ＜0时：β=-||

根据解析几何，若过原点作垂直于极限状态平面的法线N，设该法线N 与极值状态平面的交点为P* ，显然P*点是极限状态平面上离原点最近的点。的方向角（亦即N 的方向角）为θ1、θ2、…、θn，的长度为l（图4-57），则该极限状态平面的法线式方程为

由于方程式（4-206）和式（4-207）表示同一平面，故两方程中的对应项系数应成比例，即

式中比值q 称为法线化因子。

则有：

取式（4-209）中前n 式两端平方相加得

则得法线化因子q 为

式中根号前的符号，应根据式（4-209）中最后一个等式，取与的异号。

由于式（4-206）可改写为

用q 同乘式（4-211）的前后两部分，可得

由上式或式（4-209）、式（4-210）可知，在新坐标系中，原点到极限状态平面的最短距离l 及（法线N）的方向余弦分别为

对比式（4-195）和式（4-213）可看出，可靠指标β与l 存在以下关系

其中当基本变量的均值点（μ1，μ2，…，μn）位于可靠区，亦即时，式（4-215）取正号；反之取负号（参见图4-57）。但应注意，当取负号时β＜0，意味着结构的失效概率pf 很大，这种情况在一般工程结构设计中是不允许的。由表4-46知，通常结构要求的β值达2.7～4.2。

由式（4-215）可见，可靠指标β的绝对值就是标准正态坐标系中原点到极限状态平面的最短距离。当状态函数Z = g（μ1，μ2，…，μn）≥0时，可靠指标β等于标准正态坐标系原点到极限状态平面的最短距离；反之，β则为该最短距离的负值。根据β的这一几何意义，验算点法就把求可靠指标β的计算转化为求新坐标系中原点到极限状态面最短距离的计算，即使原来对失效概率pf需求复杂的积分问题化为求β的几何问题。

由于在结构设计中，一般要求可靠指标β≥2.7，而当β＞0时，不难说明，在构成空间的失效区内，极限状态面上离原点最近的P*点处的联合概率密度值最大，故P*点是最可能失效点，亦即基本变量取这组组合时，结构最可能导致破坏。因此，我们称这一特定点P*为“设计验算点”。

对于“设计验算点”P* ，其各坐标满足下列关系：

由式（4-205），P*点在原坐标系OX1X2…Xn 中的坐标为：

对于多个相互独立的正态分布随机变量情况的可靠度计算，仍是将随机变量Xi 作标准化处理，在新的标准正态坐标系下，极限状态方程式为一极限状态面，它将n 维空间分成可靠区［g（·）≥0］和失效区［g（·）＜0］分成两部分。经过类似推导，可得到形式上与式（4-195）相近的可靠指标β的表达式。但须采用迭代法才能求得β值，再由pf =φ（-β）求出结构的失效概率。采用验算点法，只要极限状态面是平面，所求得的失效概率就是精确值，否则是近似结果。近似值的近似程度取决于极限状态面与过P*点的切平面的偏离程度。偏离小，pf 的计算误差小；反之则增大。

对有非正态随机变量情况的可靠指标计算。在实际工程结构设计中，有些基本变量可能为非正态分布，如极值Ⅰ型分布、对数正态分布等。这时为了应用前述验算点法，需先将非正态随机变量转化为当量正态分布的随机变量（当量正态化须满足一定条件）。在非正态变量当量正态化以后，即可用所求得的当量正态变量的均值和标准差替代原变量的均值和标准差，按前述正态变量的情况计算可靠指标β。由于非正态变量的当量正态化是在设计验算点P*上进行的，而P*点在求得β之前是未知的，因此在迭代计算β的过程中，当量正态分布变量的σ'i、μ'i 也需随P*点的修正而修正。

对变量相关情况的可靠指标计算，可以通过适当的数学变换将彼此相关的基本变量转化为互不相关的随机变量，然后再按上述方法计算可靠指标β。

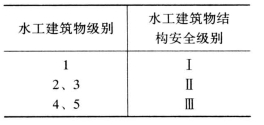
（七）结构安全级别

不同级别水工建筑物应具有不同的可靠度。在应用可靠度法对水工混凝土结构设计时，是根据水工建筑物的级别，采用相应的水工建筑物结构安全级别，从而给出不同的结构重要性系数，用以保证级别较高的建筑物有较高的可靠度。水工建筑物结构安全级别划分为三级，按表4-45 采用。

对有特殊安全要求的水工建筑物，其结构安全级别应经专门研究确定。

表4-45　水工建筑物结构安全级别

（八）目标可靠指标

目标可靠度又称设计可靠度，是依据规范设计的结构应达到的可靠度。显然，目标可靠度对应的可靠指标即为目标可靠指标。按目标可靠度所设计的结构，应是既安全可靠，又经济合理的结构。具体方法是使结构和构件在设计基准期内，在规定的条件下，使失效概率低于一个允许的水平，即

式中：［pf］为允许的失效概率。

当用可靠指标β表示时，则

式中：βT 为允许的可靠指标，也称目标可靠指标。

从理论上讲，目标可靠度应根据结构的重要性、失效后果、破坏性质、经济指标等因素以优化方法分析确定。但由于问题的复杂性和统计资料不够充分，现阶段人们还主要依赖“校准法”确定目标可靠度。

校准法就是对原规范设计和施工的结构进行反演分析，得出隐含于原规范的总体可靠度水平，并据此来确定新规范所拟采用的目标可靠度。

校准法是现阶段确定目标可靠度的一种比较切实可行的方法，也是目前国内外编制新规范共同采用的方法。它的实质就是根据实践经验，从总体上继承原规范的设计可靠度水准，认为相应于原规范的结构可靠度总的来说是合理的、可以接受的，而对不合理的地方进行局部调整。

校准法确定目标可靠指标βT 所遵循的原则为：

（1）通过对原规范设计和施工的结构进行反演分析，得出隐含于原规范的总体可靠度水平，然后，在统计分析的基础上针对不同情况作适当调整，确定合理且统一的目标可靠指标βT。

（2）安全级别愈高，目标可靠指标βT 应愈大。

（3）延性破坏构件的目标可靠指标βT 可稍低于脆性破坏构件的目标可靠指标。因为延性破坏的构件在破坏前有明显的预兆，如构件已出现裂缝、较大变形，并逐渐发展等，破坏过程较缓慢。属于延性破坏的有钢筋混凝土受拉、受弯等构件。而脆性破坏则带有突发的性质，构件在破坏前无明显的预兆，一旦破坏，其承载力急剧降低甚至断裂，例如轴心受压、受剪、受扭等构件。所以延性破坏构件的目标可靠指标可稍低于脆性破坏构件的目标可靠指标。

（4）承载能力极限状态下的目标可靠指标βT 应高于正常使用极限状态下的目标可靠指标。因为承载能力极限状态是关系到结构构件是否安全的根本问题，而正常使用极限状态的验算则是在满足承载能力极限状态的前提下进行的，只影响到结构构件的正常使用性。

校准法确定目标可靠指标的具体步骤如下。

（1）按各类水工结构选出典型构件作为校准法计算的对象；

（2）按建筑物的安全级别分组；在每一组的构件中，按它们在工程中用量的多少、造价的大小，并结合工程经验判定其各自的加权系数ωi；

（3）以原规范的安全系数对上述典型构件进行设计；

（4）确定其荷载效应S 及截面抗力R 的统计参数和概率分布模型；

（5）按前述近似概率法分别算出这些典型构件的可靠指标β1i；

（6）求出一组构件的加权平均可靠指标β1，

（7）对已建成的若干典型工程的构件，也按安全级别分组，重复（4）～（6）步骤，计算出实际工程的每组构件的加权平均可靠指标β2；

（8）根据β1 及β2 综合考虑安全与经济的最佳平衡，确定出不同安全级别的结构目标可靠指标βT。

在《水工混凝土结构设计规范》中，按承载能力极限状态（持久状况）设计时的目标可靠指标βT，是运用近似概率法对由原规范（SDJ20—78）设计出的7 种典型钢筋混凝土构件（轴心受压、大偏心受压、小偏心受压、受弯、受剪、轴心受拉、小偏心受拉）在5种不同材料组合及5种不同荷载组合（还考虑每种荷载组合中的若干不同永久荷载与可变荷载的比值）下，按上述方法一一进行分析计算，并进行统一调整后得出了表4-46中的目标可靠指标βT。

表4-46 中的结构安全级别按表4-45 确定。

表4-4　6　水工结构的目标可靠指标βT 及相应的pf（持久状况结构承载能力极限状态）

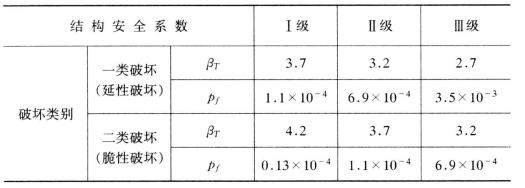
前已述及，荷载与材料强度是分别影响荷载效应和结构抗力的主要因素，且都是随机变量。由于它们具有统计的规律性，在确定结构设计所用的荷载值和材料强度指标时，可依据其概率分布曲线，并采用两个非常重要的统计参数，即平均值μ和标准差σ分析得出。

（九）结构可靠性分析的步骤

结构可靠性的分析步骤如下。

1.确定概率模型（概率分布模型、统计参数）

搜集有关结构可靠性影响因素——基本变量X1，X2，…，Xn 的观测或试验资料，通过概率统计分析确定各基本变量的概率模型（包括概率分布型式和统计参数）。结构可靠性分析所涉及的随机因素主要来自三个方面：作用、材料性能和结构的几何参数。

2.建立极限状态方程

采用结构计算或试验的方法进行结构分析，研究结构各种功能的失效机理、失效模式，据此建立相应的极限状态方程。

3.计算结构的可靠度并校核其是否满足目标可靠度

有关结构的作用的随机性、材料性能的随机性和几何参数的随机性可参考有关文献。

三、水工混凝土结构设计规范的实用设计表达式

新编的《水工混凝土结构设计规范》［19］采用以概率为基础的极限状态设计方法，以可靠指标β度量结构构件的可靠度。如前所述，β值的计算非常复杂，需要大量的统计信息，直接在设计中应用就很不方便，新的水工混凝土结构设计规范的作法是采用分项系数的实用设计表达式。设计人员可不必直接计算可靠指标β，只要按该规范给定的各分项系数进行计算，则所设计的结构构件，其隐含的可靠指标β就能满足不小于目标可靠指标βT的要求。

前已述及，从可靠度的观点看，水工混凝土结构设计的极限状态分为承载能力极限状态和正常使用极限状态两种。所以，其分项系数的表达式也有两种。

（一）承载能力极限状态设计表达式

新编的水工混凝土结构设计规范规定，按承载能力极限状态设计时，应考虑以下两种荷载效应组合。

1.基本组合

基本组合是持久状况或短暂状况下永久荷载与可变荷载的效应组合。

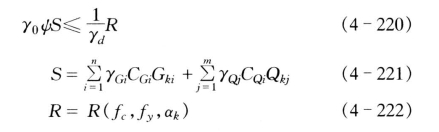
对于基本组合，承载能力极限状态设计表达式为上述三式中：γ0 为由结构安全级别确定的结构重要性系数，对应于结构安全级别为Ⅰ、Ⅱ、Ⅲ级的结构构件，分别为1.1、1.0、0.9；ψ为对应于持久状况、短暂状况、偶然状况的设计状况系数（可分别取1.0、0.95、0.85）；S 为荷载效应组合设计值；R 为结构构件抗力设计值；γd 为由结构破坏的性质确定的结构系数，按表4-47取用；γG、γQ 分别为永久荷载与可变荷载的分项系数，由《水工建筑物荷载设计规范》并按《水工混凝土结构设计规范》的规定取用；Gk、Qk 分别为永久荷载与可变荷载的标准值，按《水工建筑物荷载设计规范》取用；CG、CQ分别为永久荷载与可变荷载的荷载效应系数（即荷载与内力之间的转换系数）；R（·）为结构构件的抗力函数；fc、fy 分别为材料强度的设计值，按表4-48、表4-49、表4-50 取用；αk 为结构构件几何参数的标准值。

表4-47　承载能力极限状态设计时的结构系数γd 值表

注　1.承受以永久荷载为主的构件，结构系数γd 应按表中数值增加0.05。但承受土重和土压力为主的构件可不增加。
2.对新型结构，结构系数γd 可适当提高。

应当指出，上列式中n 个永久荷载及m 个可变荷载都是分别指有可能同时出现的荷载，如不能同时出现，就不应组合在一起。结构构件有不同设计状况时，则应分别按不同状况计算荷载效应。

仍以图4-55 承受均布荷载（自重gk 和活载Qk）的单筋矩形截面简支梁跨中正截面承载力设计为例，原规范的公式（4-159）可用新规范（采用新符号）的表达式则为

式中：S 称为荷载效应，即结构可能同时受到作用的各种荷载在构件上产生的效应。广义的荷载效应是指构件在承载后产生的内力、变形、裂缝宽度等。对承载能力计算来说，荷载效应是指构件计算截面上产生的内力（弯矩、轴力、剪力等）。荷载效应S由永久荷载Gk 及可变荷载Qk 乘以各自的荷载效应系数CG 及CQ求得，此处CG即为（1/8）l2；CQ即为（1/4）l。

式中R称为截面抗力，其中Rh 为混凝土的设计强度、Rg为钢筋的设计强度，它们是按保证率为97.72%得出的。α为结构尺寸因素，此处即为Ag、h0、b等值。

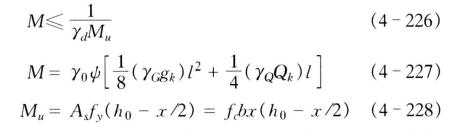
式中：Mu为截面破坏时的极限弯矩；fy为钢筋强度的设计值；fc 为混凝土轴心抗压强度的设计值。

2.偶然组合

偶然组合是偶然状况下永久荷载、可变荷载与一种偶然荷载的效应组合。

对于偶然组合，承载能力极限状态设计表达式为

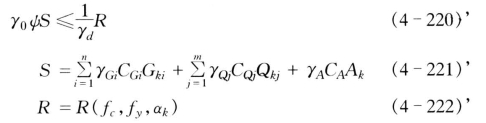
式中：ψ为对应于偶然组合的设计状况系数，取0.85；γA 为偶然荷载作用的分项系数；CA 为偶然荷载效应系数；Ak 为偶然荷载的标准值；其余符号同上。

对于偶然组合，承载能力极限状态设计表达式按下列原则确定：

（1）偶然荷载的分项系数取为1.0；

（2）参与组合的某些可变荷载，可根据各类水工建筑物设计规范的规定作适当折减；

（3）结构系数γd 值可按表4-47取用。

在承载能力极限状态计算中，内力N、M、V、T 等的设计值应是各荷载标准值乘以相应的荷载分项系数后所产生的效应总和并再乘以结构重要性系数γ0 及设计状况系数ψ后的值。

（二）正常使用极限状态设计表达式

正常使用极限状态的验算是要保证结构构件在正常使用条件下，裂缝宽度和挠度不超过相应的允许值。对于有抗裂要求的构件在正常使用条件下还应满足抗裂要求。

由于正常使用极限状态的验算是在承载力已有保证的前提下进行的，其可靠度要求较低，一般要求β=1.0～2.0。所以，与承载能力极限状态相比，材料强度的保证率可适当降低，采用材料强度的标准值而不用设计值，即材料分项系数取为1.0。计算荷载效应时，荷载分项系数γG 及γQ 一律取为1.0。结构系数γd 及设计状况系数ψ也均取为1.0。

由于荷载作用时间的长短将影响对抗裂验算的要求、裂缝宽度和变形的大小，因此在正常使用极限状态验算时，应按荷载效应的短期组合及长期组合分别验算。

短期组合，即指持久状况或短暂状况下，包括短期作用在内的全部可变荷载的效应与永久荷载的效应的组合；长期组合，即指持久状况下，可变荷载中长期作用的那部分荷载（即荷载的准永久值）的效应与永久荷载的效应的组合。两个组合所产生的荷载效应大小不同，前者除永久荷载外，全部可变荷载加以组合；后者则是除永久荷载外，可变荷载中长期作用的那部分加以组合。所以，短期组合的荷载效应值比长期组合的荷载效应值要大。所要求的功能限值也可不同。例如，对有限制裂缝宽度要求的构件，在荷载效应的长期组合下的允许裂缝宽度值就比短期组合下的允许裂缝宽度值控制得严一些。两个组合的表达式分别为：

式中：c1、c2 分别为结构裂缝宽度与挠度的限值；Ss（·）、Sl（·）分别为荷载效应短期组合与长期组合时的功能函数；fk为材料强度的标准值，按表4-48、表4-49取用；ρ为可变荷载标准值的长期组合系数，可参照有关荷载规范的规定及工程经验取用。

必须注意，在水工混凝土设计规范中，所指的正常使用极限状态计算中，短期组合时的内力值Ns、Ms 等是指由各荷载标准值所产生的荷载效应总和并乘以结构重要性系数γ0 后的值；长期组合时的内力值Nl、Ml 等是指由各荷载标准值并考虑荷载长期组合系数后所产生的荷载效应总和再乘以结构重要性系数γ0后的值。

由上述可知，只要正确选用荷载和材料的标准值及五个分项系数，用以上表达式就能正确进行结构的可靠度设计。

四、荷载的标准值

作用于水工建筑物上的荷载，按其随时间的变异性和出现的可能性不同，可分为以下三类。

（1）永久荷载，指大小不随时间变化，或变化与其平均值相比可以忽略不计的荷载，如结构自重、土重、固定设备等。

（2）可变荷载，指大小随时间变化的幅度较大，与其平均值相比不可忽略的荷载，如吊车荷载、楼面堆放荷载、静水压力、楼面人群荷载、风荷载等。

（3）偶然荷载，指在设计基准期内不一定出现，但它一旦出现，其量值很大、且持续时间较短的荷载，如地震、爆炸等。

结构设计中所涉及的荷载，可采用随机变量或随机过程的模式加以描述。荷载可以根据不同极限状态的设计要求，采用不同的荷载代表值，一般荷载有标准值、准永久值和组合值三种代表值。其中标准值是荷载的基本代表值，而其他两种代表值是以标准值乘以相应的系数后得到的。

1.荷载标准值

荷载标准值Sk 是指在设计基准期、正常运用情况下可能作用于结构构件上的最大荷载值，国际上习惯称其为荷载的特征值。由于荷载本身具有随机性，因而这一最大荷载也是随机变量。荷载标准值Sk 由设计基准期内荷载最大值概率分布的某一分位值来确定，设计基准期一般规定为50年。荷载S 的统计曲线如图4-58 所示，由此可得

图4-58　荷载S 的概率分布曲线

式中：μs 为荷载的统计平均值；σs 为荷载的统计标准差；δs 为荷载的变异系数，αs为荷载标准值的保证率系数。

国际标准化组织（ISO）建议取αs=1.645，此时荷载标准值即相当于具有95%保证率的0.95 分位值（假定荷载为正态分布）。即作用在结构构件上的实际荷载超过荷载标准值的可能性只有5%。

但实际上并非所有的荷载都已经或能够取得完备的统计资料，并能通过合理的统计分析来规定其标准值的。对不少荷载，还不得不根据已有的工程实践经验和沿用的数值，经过分析判断确定其标准值。

我国GBJ9—87《建筑结构荷载规范》就是按上述两种方法确定荷载标准值的。对于按荷载概率分布取值的，规范也没有规定统一的分位值，这主要是考虑到所确定的荷载标准值不宜与过去规定的相差太远，以免设计出的结构，材料用量变动过大。

水工建筑物荷载的标准值应根据《水工建筑物荷载设计规范》取用。

2.荷载准永久值

荷载作用的时间长短直接影响着结构的变形和裂缝宽度。因此，在按正常使用极限状态计算时，将荷载效应分为短期组合及长期组合进行验算。在考虑长期组合时，永久荷载是一直作用的，而可变荷载不像永久荷载那样在结构设计基准期内全部以其最大值经常作用在结构上，而是时大时小，作用持续的时间又是时长时短。因此，在考虑长期组合的荷载效应时，可变荷载不应取其标准值作为它的代表值，而应取其“准永久值”作为它的代表值。所谓荷载的“准永久值”是指可变荷载在结构设计基准期T 内经常作用的那一部分荷载，它对结构的影响类似于永久荷载，达到和超过准永久值的总持续时间与整个设计基准期的比值一般取为不大于0.5。

可变荷载的准永久值可由可变荷载标准值Qk 乘以相应的长期组合系数ρ（≤1）得出，即可变荷载的准永久值可写成为ρQk，ρ由有关荷载规范给出。可见，荷载准永久值实际上是考虑荷载效应的长期组合而对可变荷载标准值的一种折减。

3.荷载组合值

应注意，此处的荷载组合值与以往教科书上的荷载组合是不同的。当结构构件承受两种或两种以上的可变荷载时，考虑到各种可变荷载不可能同时以其标准值（最大值）出现，因此除了一个主要可变荷载外，其余可变荷载标准值应乘以小于1的组合系数，以对可变荷载标准值进行折减，使结构构件在两种或两种以上可变荷载参与组合的情况下与仅有一种可变荷载参与组合的情况具有大致相同的可靠指标。

GBJ9—87《建筑结构荷载规范》将可变荷载组合值记为ψcQk，其中Qk 为某种可变荷载标准值，ψc 为组合系数。但目前，尚无足够资料能确切地得出不同的荷载组合时的组合系数，因此该规范仅规定了综合的荷载组合系数：当有风荷载参与组合时，可变荷载的组合系数ψc 取为0.6；当无风荷载参与组合时，则组合系数全部取为1.0。

在水工结构设计中，因其风荷载在总荷载效应中所起的作用与工业民用建筑结构有所不同，且习惯上均不考虑可变荷载组合时的折减，因此《水工混凝土结构设计规范》给出的荷载效应设计表达式也就没有采用可变荷载组合值，即对参与组合的全部可变荷载都不乘以组合系数而直接采用其标准值（相当于取组合系数等于1）。由此，在设计计算中，可能造成与仅有一种可变荷载组合情况下的结构可靠度的不一致性，此问题还有待于进一步研究。

五、材料强度的标准值

材料强度的标准值以材料强度概率分布的某一分位值来确定。在国际上也称为材料强度特征值。当材料强度服从正态分布时，其标准值可由下式计算

式中：μf 为材料强度的统计平均值；σf 为材料强度的统计标准差；δf 为材料强度的变异系数，α为材料强度的保证率系数。

按照国际标准（ISO3893）的规定，材料强度的标准值由材料强度概率分布的0.05 分位值来确定，即材料的实际强度小于强度标准值的可能性只有5% ，也就是强度标准值具有95%的保证率，对应的保证率系数α= 1.645 如图4-59所示。

图4-59　材料强度的标准值的取值

（一）混凝土强度标准值

1.混凝土立方体抗压强度标准值fcuk

混凝土立方体抗压强度标准值亦称混凝土强度等级，它具有95%的保证率。其值由下式决定

式中：μfcu、σfcu、δfcu分别为混凝土立方体抗压强度的统计平均值、统计标准差和变异系数。

根据对国内部分水利水电工程的调查统计，一般构件的C15、C20、C25、C30 等级水工混凝土立方体抗压强度的变异系数δfcu值大致为0.20、0.18、0.16、0.14。

2.混凝土轴心抗压强度标准值fck

国内试验研究表明，混凝土棱柱体轴心抗压强度平均值μfc与边长为150mm立方体抗压强度平均值μfcu之间的关系为

在实际构件中混凝土的受力情况和棱柱体混凝土试块的受力情况稍有差异，体积大小和加载速度亦不一样。所以考虑实际构件和试块的差异，尚需乘一个折减系数。根据试验数据分析及参考国内外有关规范的规定，水工混凝土结构设计规范取这一折减系数为0.88。即构件中的混凝土轴心抗压强度平均值μfc为

由此，轴心抗压强度标准值则为

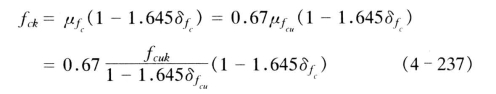
假定δfcu=δfc，则

考虑到较高强度等级混凝土的脆性破坏特征比较显著和实践经验不足，对C45、C50、C55 和C60 等级的混凝土轴心抗压强度标准值按上式计算后，再分别乘以系数0.975、0.95、0.925和0.9。由此，可得出不同强度等级混凝土的轴心抗压强度标准值fck，见表4-48。其值与国家标准GBJ10—89《混凝土结构设计规范》中规定是一致的。

表4-48　混凝土强度标准值（N/mm2）

3.混凝土轴心抗拉强度标准值ftk

试验研究表明，混凝土轴心抗拉强度平均值μft与边长为150mm立方体抗压强度平均值μfcu之间的关系为

同样，考虑到构件中的混凝土强度与试件混凝土强度的差异，取折减系数为0.88，因此构件中的混凝土轴心抗拉强度平均值μft为(www.xing528.com)

假定δft=δfcu，混凝土轴心抗拉强度标准值则为

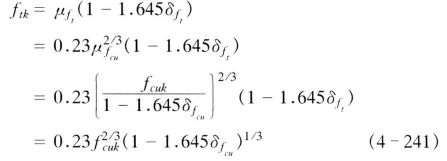
同样，考虑到较高强度等级混凝土的实践经验不足，对C45、C50、C55 和C60 等级的混凝土轴心抗拉强度标准值按上式计算后，再分别乘以系数0.975、0.95、0.925 和0.9。最终得出混凝土轴心抗拉强度标准值ftk，见表4-48所列。

（二）钢筋强度标准值

为了使钢筋强度标准值与钢筋的检验标准统一起见，受拉热轧钢筋采用国家标准（GB13013—91、GB13014—91、GB1499—91）规定的屈服强度作为标准值fyk（fpyk）（对预应力钢筋用fpyk和fptk表示），国标规定的屈服强度即钢筋出厂检验的废品限值，其保证率不小于95%。对于无明显屈服点的钢筋，如钢丝、钢绞线、热处理钢筋及冷轧带肋钢筋，为了与国家标准的出厂检验强度一致起见，采用国标规定的极限抗拉强度作为标准值fstk（fptk），其保证率也不小于95%。

钢筋、钢丝、钢绞线的强度标准值见表4 -49、表4 -50。其数值与国标GBJ10-89规范的取值相同。

表4-49　钢筋强度标准值（N/mm2）

续表

表4-50　钢丝、钢绞线强度标准值（N/mm2）

注　1.碳素钢丝系指国家标准GB5223—95《预应力混凝土用钢丝》中的消除应力的高强度圆形钢丝。
2.钢绞线直径d 系指钢绞线截面的外接圆直径，即公称直径。
3.根据国际标准，同一规格的钢丝（钢绞线）有不同强度级别，因此表中对同一规格的钢丝（钢绞线）列出了相应的fptk值，在设计中可自行选定。

既然影响结构可靠（安全）性的各因素（如Gk、Qk、l、b、h、Ag、Rg、Rω 等等）都是随机变量，因此式（4-223）中，荷载效应S 及截面抗力R 也是随机变量。它们的取值也应该用概率来描述。

六、分项系数

在上述的设计表达式中采用了五个分项系数，用以构成并保证结构的设计可靠度。

1.结构重要性系数γ0

建筑物的结构构件安全级别不同，其对目标可靠指标的要求也不同（见表4-46）。为此，在设计中应将荷载效应值乘以结构的重要性系数γ0。通过结构可靠度分析，水工混凝土结构设计规范给出了结构安全级别为Ⅰ、Ⅱ、Ⅲ级的结构重要性系数γ0 值分别为1.1、1.0 和0.9。

2.设计状况系数ψ

结构在施工、运行、检修等不同时期可能出现不同的结构体系、荷载及环境条件，所以在设计时应考虑下列三种设计状况。

（1）持久状况。在结构运行使用过程中，不仅出现且持续时间很长，一般与设计基准期为同一量级的设计状况。

（2）短暂状况。在结构施工（安装）、检修或使用过程中短暂出现的设计状况。

（3）偶然状况。在结构使用过程中，出现概率很小、持续很短的设计状况。

例如，肋拱渡槽的拱肋，一般侧卧于地面上分段预制，每段起吊和空中翻身及就位之前均为仅承受自重的双悬臂曲梁；吊装就位后为仅承受自重的简支曲梁；拱肋接头及支座处伸出的钢筋焊接、浇筑的二期混凝土达到一定强度并拆除支架后，为仅承受自重的裸拱；当拱上排架、槽身等吊装、施工过程中，为受短期荷载的肋拱；施工结束并通水，为承受各种相应荷载的肋拱结构。其中，吊装验算时为短暂设计状况，正常应用的各种情况即为持久状况，若位于地震区，受地震荷载作用时即为偶然状况。

上述三种设计状况均应进行承载能力极限状态设计。对持久状况尚应进行正常使用极限状态设计，对短暂状况要不要进行正常使用极限状态设计，可根据具体情况决定。对偶然状况则可不进行正常使用极限状态设计。

不同设计状况对可靠度水平的要求也不同，在设计表达式中由ψ反映。水工混凝土结构设计规范给出，对应于持久状况、短暂状况、偶然状况的设计状况系数ψ值分别为1.0、0.95 和0.85。

3.荷载分项系数γG、γQ

从理论上讲，结构构件在其使用期间，实际荷载仍有5%的可能超过预定的标准值。为了考虑这一最不利情况，在承载能力极限状态设计表达式中还引入一个荷载分项系数（一般都大于1，个别情况也可小于1），主要是用来考虑荷载超过标准值的可能性。在水工建筑物设计中，其实质上就是“超载系数”，但也适当反映了结构可靠度要求。

荷载设计值为荷载标准值乘以相应的荷载分项系数。若永久荷载和可变荷载的标准值分别为Gk、Qk，相应的荷载分项系数分别为γG、γQ，则永久荷载和可变荷载的设计值可分别记为γGGk 及γQQk。

严格讲，荷载设计值也应由荷载之概率分布的某一分位值来确定，应比荷载标准值具有更大的保证率。但目前，对大部分荷载来说，还没有足够完备的统计资料。因此，也无法采用统一的保证率系数，使所有荷载的设计值均处于同一保证率水平上。

显然，在永久荷载和可变荷载的分项系数γG、γQ 的确定中，应考虑结构构件所承受荷载的变异程度大小。对永久荷载，如构件自重等，变异性很小，其荷载分项系数就应取得较小。在作用过程中能够控制其不超出规定限值的某些可变荷载，如水闸的闸门额定启门力、溢洪道挡水的水压力、开口渡槽的满槽水荷载及水池水荷载等不可能发生超载的情况，对这些变异性不大或能严格控制其最大值的可变荷载，荷载分项系数显然也应取得小些。对像人群荷载、楼面堆货、车辆荷载等不能控制或难以控制的可变荷载，不仅大小经常变化，且变化幅度比较大，其分项系数就应取一较大的值。对于风载、雪载等变异性更大的自然界的一些可变荷载，其荷载分项系数还应取得更大一些。当永久荷载对结构可靠性有利时，荷载分项系数则应取为小于1的数值。

荷载分项系数按《水工建筑物荷载设计规范》取用。但应注意，在使用该规范进行结构构件计算时，还应按该规范的规定，对某些可控制其不超出规定限值的可变荷载，如荷载规范所规定的分项系数γQ 小于1.10时，则应取为1.10；对其他可变荷载，如所规定的分项系数γQ 小于1.20 时，则应取为1.20。这主要考虑按水工混凝土结构设计规范设计的结构构件的材料用钢量与过去水平相比，不致有过分的锐减，以及保证必要的设计延续性。对于该规范未予规定的荷载，其分项系数可按表4 -51 取用。当永久荷载的效应对结构有利时，γG 应取为0.95。

表4-51　荷载分项系数

4.混凝土和钢筋的强度分项系数γc、γs

为了充分考虑材料的离散性及不可避免的施工偏差等因素使材料的实际强度低于其强度标准值的可能性，在承载能力极限状态计算中又引入混凝土强度分项系数γc 及钢筋强度分项系数γs。

材料强度标准值除以相应的材料强度分项系数后，即为材料强度设计值。混凝土和钢筋的强度设计值可分别表示为

根据我国GB50199—94《水利水电工程结构可靠度设计统一标准》的规定，材料强度设计值原应取为强度总体分布的平均值减去α1 倍标准差，即

式中α1 为材料强度设计值的保证率系数。材料强度设计值应比材料强度标准值具有更高的保证率。例如原水工钢筋混凝土结构设计规范（SDJ20—78）取α1=2，相应的材料强度设计值的保证率即为97.72%。理论上讲把α1 取为某一固定值比较合理，这样，不同材料的强度设计值就可处于同一保证率水平。但按这一原则确定的设计值与国家标准GBJ10—89《混凝土结构设计规范》中的取值就有差异，会给工程技术人员带来理解上的不便，易在设计中发生混乱。所以水工混凝土结构设计规范将混凝土和钢筋的强度分项系数及强度设计值取得与GBJ10—89 规范相同，即：

（1）对混凝土，取强度分项系数γc =1.35。因此，混凝土轴心抗压强度设计值fc=fck/γc=fk/1.35；混凝土轴心抗拉强度设计值ft =ftk/γc=ftk/1.35。其中fck及ftk为混凝土轴心抗压强度及轴心抗拉强度的标准值。

（2）对热轧Ⅰ级钢筋，取强度分项系数γs=1.15，钢筋强度设计值fy=fyk/γs=fk/1.15；对热轧Ⅱ、Ⅲ、Ⅳ级钢筋，取γs=1.10，则fy=fyk/1.10。

为了应用方便，规范中直接给出了混凝土强度设计值（见表4-52）、钢筋、钢丝及钢绞线的强度设计值（见表4-53、表4-54）可直接查用。在材料强度设计值中已隐含了材料分项系数。

表4-52　混凝土强度设计值（N/mm2）

表4-53　钢筋强度设计值（N/mm2）

注　1.按照国家标准编制方法的规定，不在设计规范中再规定钢筋符号，本表中钢筋符号是参考过去习惯用的符号列出的。其中中R为江苏省地方的符号。
2.在钢筋混凝土结构中，轴心受拉和小偏心受拉构件的钢筋抗拉强度设计值大于310 N/mm2时，仍应按310 N/mm2取用，其他构件的钢筋抗拉强度设计值大于360 N/mm2时，仍按360 N/mm2取用；对于直径大于12mm的Ⅰ级钢筋，如经冷拉，不得利用冷拉后的强度。
3.LL550级冷轧带肋钢筋经机械调直后，抗拉及抗压强度设计值应降低20 N/mm2。

表4-54　钢丝、钢绞线强度设计值（N/mm2）

注　碳素钢丝、刻痕钢丝、钢绞线的强度标准值不符合表4-50的规定时，其强度设计值应进行换算c

表4-55 和表4-56 分别给出了混凝土和钢筋的弹性模量。

表4-55　混凝土弹性模量Ec（N/mm2）

表4-56　钢筋弹性模量（N/mm2）

5.结构系数γd

在承载能力极限状态设计中引入结构系数，用以考虑因结构构件的荷载效应计算模式、几何尺寸和结构构件抗力计算模式等的不定性以及荷载分项系数与材料强度分项系数未能考虑到的其他各种变异因素的影响。

结构系数是直接与结构构件的可靠度水平挂钩的。因为，荷载分项系数和材料强度分项系数已事先选定，所以可根据可靠度理论，由给定的目标可靠指标，用近似概率法，确定设计表达式中的结构系数γd 值。

对于每一种结构构件，不同材料组合，不同荷载组合，由于其变异性不同，按规定的目标可靠指标求得的结构系数是不同的。为了使最终确定的结构系数为最优值，即按此结构系数和事先选定的荷载分项系数以及材料强度分项系数所设计的结构构件，在不同的设计条件下均能较好地接近目标可靠指标，在计算结构系数时选择了水工钢筋混凝土结构中常用的七种典型构件进行研究，并考虑了五种不同材料组合和五种不同荷载组合及若干个可变荷载效应与永久荷载效应的比值ρ。对于每一结构构件，最后取不同材料组合与不同荷载组合及不同ρ值下的结构系数的加权平均值作为此种典型构件最终的结构系数。

《水工混凝土结构设计规范》规定的结构系数γd 值见表4-47。

应特别注意，在分项系数实用设计方法中，水工混凝土结构设计规范中所采用的荷载分项系数与用于建筑工程的国标GBJ10—89《混凝土结构设计规范》中的荷载分项系数是完全不同的。由于不同规范中的一些系数因其导出条件不同而自身配套，所以设计中不能彼此混用。

【实例4-6】　渡槽排架结构安全复核

一、基本资料

在一座中型水库向灌区输水的干渠上，建有一座跨越一洼地的简支梁式渡槽［20］。渡槽设计流量Q0=10m3/s，加大流量Qm=11.9m3/s。渡槽为3级建筑物。其布置及结构尺寸如下。

槽身：采用U 形钢筋混凝土结构，槽身横断面结构尺寸见图4-60。槽壳直段高f =0.94m，内半径R0=1.4m，厚度t=0.12m。槽端设支承肋，肋厚0.3m。槽壳从端肋向外伸出0.1m以便设止水。槽身端肋间净距l=10.20m，一节槽身总长度Lj=10.20+0.3×2+ 0.2= 11.00m。每节槽身设拉杆8 根，其间距S=1.5m，截面高0.2m、宽0.15m。槽顶栏杆柱截面为0.12×0.12m2，栏杆纵杆截面为0.1×0.08m2。其余尺寸见图。

排架：由于渡槽高度不大，故均采用单排架支承，排架间距Lp=11.00+0.06=11.06m，最大排架高度12.20m，基础为板基。最大高度排架的结构尺寸见图4-61。

作用于槽身、排架上的荷载主要有结构自重、槽中水重、槽顶人群荷载及槽身与排架上的风荷载。计算中，取钢筋混凝土的容重γh =25kN/m3，水的重度γ=10 kN/m3，槽顶人群荷载按2 kN/m2 计算。渡槽所在位置的最大风速按9级，取v=24m/s。

试计算排架的内力和复核其配筋，即进行承载力的复核。

二、荷载计算

作用于排架上的荷载：槽身自重、槽内水重、槽顶人群荷载、槽身及排架深度风荷载等。

荷载计算公式：

图4-60　U 形槽身横断面图（单位：cm）

式中：γ0 为结构重要性系数，建筑物为3 级，其对应安全级别为Ⅱ级，故γ0 =1.0；ψ为设计状况系数，本例为持久设计状况，取ψ=1.05；γG 为永久荷载分项系数取1.05；γQ 为可变荷载分项系数取1.20。

图4-61　渡槽排架结构布置图（单位：cm）

1.槽身自重

2.满槽水重

3.人群荷载

槽顶人群重：

4.排架重

5.风荷载

横向风压力可按下式计算

式中：K 为风载体形系数，与建筑物的体形、尺度等有关；矩形槽身可取1.2～1.3（空槽取小值，满槽取大值）；U形槽身可取0.8～0.9（直段高度大时取大值）；圆管形断面可取0.7；本例U 形槽身因直段高度较大，取体形系数K =0.9；对于排架，取K=1.3；Kz 为风压高度变化系数，可按表4-57采用；本例中，槽身距地面高度13.80m，由表4-57 近似取风压高度系数Kz=1.15；排架迎风面形心高度约6.1m，近似取Kz =0.8；η为排架前柱对后柱的挡风系数；因排架立柱净距与立柱迎风面宽度之比为2.86/0.40 = 7.15，当此比值大于或等于10 时，不计前柱对后柱的挡风作用，即η=1.0；此处比值7.15＜10时，η值在0.2至10之间变化；本例比值为7.15，故近似取η=0.53；β为风振系数；对较高的排架式渡槽，如果其基本自振周期T ≥0.5s 时，可根据建筑物结构的类别及基本自振周期按表4-58 采用；W0 为基本风压强度。

表4-57　风压高度变化系数Kz

表4-58　风振系数β

基本风压：

作用于槽身、排架上的横向风压力分别为：

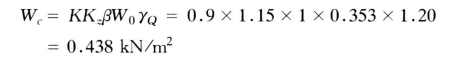
作用于整个槽身上的横向风压力为：

渡槽的自振周期T（s）按下式计算：

式中：H 为槽身高度，取1380cm；G0 为作用于排架顶部的槽身重（槽中有水时应计入水重），G0 = 353900 + 707080 =1060980 N；E 为排架材料的弹性模量，285000 kg/cm2 =2795850 N/cm2；J 为排架横截面的惯性矩，（40×303/12+40×30×1552）×2=5.784×107 cm4。

则渡槽的自振周期：

因本渡槽的高度较小，仅12.2m，且满槽水时的自振周期T 小于0.5s，当槽中无水时G0 更小，则T 值还要小，故不计风振影响，即取β=1.0。

三、排架内力计算与配筋复核

作用于排架上的荷载即排架的计算简图见图4-62。

1.对空槽加横向风压力情况

图4-62　排架内力计算简图（单位：m）

作用于排架各节点上的风压力如下：

2.对满槽水加横向风压力情况

作用于排架各节点上的风压力同上。

3.横向风压力作用下的排架内力计算

已知横梁中心距l=4m，两立柱的中心距之半= 4.55 m。

节点水平风荷：p1=6.260kN，p2=p3=0.539kN。

（1）固端弯矩：

（2）抗弯劲度

柱的惯性距：

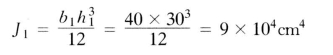
梁的惯性距：

柱的抗弯劲度：

梁的抗弯劲度：

（3）分配系数

分配系数：

（4）列表计算杆端弯矩

表4-59　力矩分配计算表

（5）剪力计算（使结点顺时针旋动，剪力为正）

（6）求轴向力（取结点平衡计算）

计算左侧柱的轴向力［图4-63（a）］：

其中G1：半根横梁及一节柱的自重，即横梁与柱的自重逐渐往下增加。

计算右侧柱的轴向力［图4-63（b）］：

计算横梁轴向力［图4-63（c）］：

同理：N22"=N33"=0说明水平向荷载反对称，横梁无轴力。

排架各的弯矩、轴力和剪力绘于图4-64。

4.排架配筋复核

（1）空槽有风时的排架配筋计算。

图4-63　排架结点平衡图

（a）左侧结点平衡图；（b）右侧结点平衡图；（c）横梁轴力计算图

1）立柱配筋。排架在横向按超静定单跨多层钢架计算，由于有横梁存在，一般不考虑柱的纵向弯曲的影响，而将每一段柱按偏心受压构件作配筋计算。由排架内力可以判断，以弯矩最大轴向力较小的43柱段最危险，对此柱段作配筋计算，由于风向的可变性，立柱均按对称配筋。

排架原设计混凝土为250 号，相当于C23。经现场检测，混凝土的实际标号为C20。故以下按C20 进行复核。

43 柱段：M43 = 16.567kN·m，N43 = 176.405 kN，b =400mm，h =300mm，l0 =4m。

a= a'= 35mm，h0 = h - a = 265mm，C20 混凝土fc =10.0N/mm2。

排架在横向风荷作用下为有侧移钢架，故按一端固定一端自由考虑（偏安全），则

l0/h=2×4000/300=26.67＞8需考虑纵向弯曲的影响。

图4-64　排架内力图

（a）弯矩图；（b）轴力图；（c）剪力图

因为所以偏心距取实际值94mm。

，取ζ1 = 1，经检测，保护层实际厚度a =35mm，则h0=h -a =300-35=265 mm。

因为l0/h＞15，所以ζ2 =1.15-0.01（l0/h）=1.15-0.01×26.67 = 0.8833

因为　ηe0=2.265×94=212.91＞0.3h0 =79.5

所以按大偏心受压构件计算。

计算A's 及As：

对于Ⅰ级钢筋，可查表得αsb=0.426，

按最小配筋率计算A's。查表得：ρmin=0.25%，

所以A's=ρminbh0=0.25%×400×265=265mm2，

实际配筋为2Φ21（A'=693mm2）。

实际采用2Φ21（A's=693 mm2），满足要求。

2）横梁配筋。横梁33"弯矩最大，M = 26.25kN·m，N =0，所以按纯弯构件配筋。在梁与柱的连接处，一般加承托以改善受力条件。横梁的配筋不应该用梁端柱中心线上的弯矩，而用承托末端的弯矩，由于弯矩随横梁长度成直线变化，所以承托末端弯矩为。

b =300mm；h =400mm；a =35mm；h0 = h - a =365mm；γd =1.2；fc=10N/mm2

实际已采用3Φ19，As=851mm2，满足要求，且考虑风荷的反向性，采用梁的上下层对称配筋。横梁22"弯矩略小于33"，配筋量与33"相同，故也满足要求。同理可对横梁11"进行配筋量的校核（此处从略）。

（2）满槽水有风时的排架配筋计算。

水平荷载与空槽有风的情况相同，即各构件的弯矩，剪力与空槽有风情况相同，满槽水时只增加了排架柱上沿直向水重，即增加了柱的轴向力。

1）对4"3"柱段配筋计算。4"3"柱段承受的轴向力较大，弯矩最大

因为e0＞，所以取e0=20.79mm

因为l0/h＞15，则ζ2=1.15-0.01（l0/h ）=0.8833

应按大偏心受压构件计算。

计算ξ值：

虽然ηe0＞0.3h0，但此时的ζ＞ζb，故仍按小偏心受压构件计算。

大于最小配筋率：

实际配筋为2Φ21（693mm2），不足所需钢筋之半，不满足要求。

2）对43柱段配筋计算。43 柱段承受的轴向力较小，弯矩也最大。

因为e0＞，所以偏心距取实际值23.65 mm

因为l0/h=26.67＞15，则ζ2=1.15-0.01（l0/h）=0.8833

应按大偏心受压构件计算。

计算ζ值：

虽然ηe0＞0.3h0，但此时的ζ＞ζb，故仍按小偏心受压构件计算。

大于最小配筋率：

实际配筋为2Φ21（693mm2），不足所需钢筋之半，不满足要求。

四、支座复核

槽身端梁与排架顶部接触面处要设置支座，以避免混凝土局部压碎，此外，当温度下降混凝土收缩时，可减少接触面上摩擦力。根据本渡槽的跨度与荷重，属于中型渡槽，决定采用钢板支座，钢板平面尺寸，初步拟定为a×b=25cm×30cm［见图4-65（b）］。

1.钢板下的混凝土平均应力

式中：G'为满槽水时一个槽身总重1060.65 kN；n 为一个槽身支承钢板个数，实际n =4，但考虑到施工的可难偏差，引起三点支承，取n = 3；a 为沿槽长方向钢板宽度，a = 25cm；b 为沿槽宽方向钢板宽度，b=30cm。

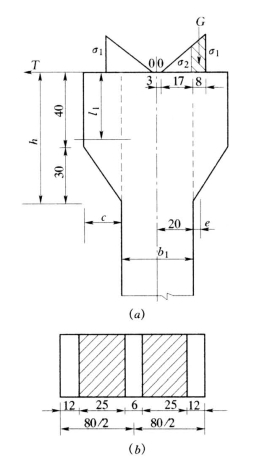
图4-65　支座牛腿及排架顶视图

（a）牛腿计算图；（b）排架顶视图

2.钢板垫底座下的混凝土允许局部抗压强度

可用下列经验公式计算

式中：K 为钢筋混凝土结构强度安全系数，Ⅳ级建筑物特殊荷载K = 1.6；fc 为混凝土棱柱体抗压强度极限C20 的Ra =14.22N/mm2；Fcm为支座钢板面积，Fcm =a×b=25×30cm2；F 为支座处受压混凝土面积。

对于槽身端梁底部支承面，F=30×30cm2

说明初步拟定的钢板尺寸是足够了。

3.支座钢板厚度计算

当槽身混凝土因温度下降而收缩，则端梁与排架顶部的钢板发生相对移动而产生摩擦力。

式中：f 为钢板之间的摩擦系数，考虑钢板柜运用时间长了生锈，取f =0.5；n 为一个槽身支承钢板个数，仍取n=3；G'的意义同前，则

支座钢板厚度计算：

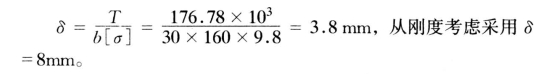
式中：［σ］为钢板的允许应力，160 N/mm2。

五、牛腿复核

1.牛腿尺寸

为了降低排架顶部接触应力，在排架头部伸出牛腿成一短悬臂梁，悬臂长度（b1 为立柱长边宽度，本立柱b1=40cm），取悬臂高度由弯矩拉力和剪力等控制，一般h ＞b，取h =70cm。

2.牛腿内力及配筋计算

（1）近似假定排架顶部三点支承，且考虑槽身产生一定挠度，钢板垫底下的混凝土应力按三角形分布，由零到σ1。

式中：G'、n、a、b 的意义同前，悬臂末端应力σ2 按直线比例为

悬臂所受剪力Q 为

剪力Q 对悬臂末端的偏心距e（即梯形重心距顶边的距离）

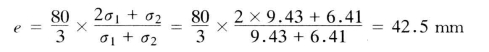
由于剪力Q 对悬臂末端产生的弯矩

由于摩擦力T 对悬臂竖向截面形而产生的弯矩

轴向拉力N = T =176.78 kN

属于大偏心受拉构件。

由于是对已有结构的承载力复核，可按以下步骤计算构件的实际承载力N。

大偏心受拉构件正截面承载力计算的基本公式为（忽略受压钢筋作用时）：

式中：各符号的意义见参考文献［4］：已配钢筋为3 ∅20，As=942 mm2；钢筋直径φ=20mm；保护层厚度a =35mm；钢板厚δ= 8mm。

则：

将各已知数据代入上式得：

上两式右端相等得：

解之得：x=1562.5＞bh0=0.614×665=408 mm

取　x=ξbh0=408mm代入求N N = 10×30（665- x2/2）/63.6 = 887.2×103　N = 887.2 kN

大于轴向拉力（摩擦力）176.78 kN。故已配钢筋满足要求。

（2）抗剪计算。已知θ=190.1 kN。

①截面尺寸复核：

因为0.25fcbh0＞γdNmax，

所以截面尺寸满足抗剪要求。

②验算是否需要按计算确定腹筋：

由SL/7507—1993《水工混凝土设计规范》第56页可知，

所以须由计算确定抗剪腹筋。

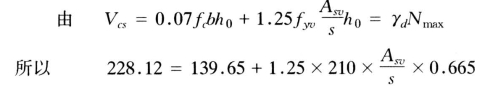
所以

选φ6@300。

因为Vs = 139.65+1.25×210×0.507×0.665 =γdNmax= 188.10 ＜228.12 kN 。

所以不需配置弯起钢筋。

六、基础复核

1.基础形式与尺寸

河床为沙卵石层，河床及两岸覆盖层不深，下层为风化的石灰岩，承载力在490kN/m2 以上，基础形式为钢筋混凝土板式基础比较合适。经检测，基础混凝土为C15，由于基础都坐落在风化的岩层上，不需要地行冲刷深度计算。

基本尺寸见图4-61。

总宽度：B=1.65m；总长度：L=4.6m；基础底板下部厚度h2=0.4m；上部杯口深度0.40m；杯口四周混凝土厚度均为0.3 m。

2.计算情况及荷载

对于基础板最不利的情况是满槽水时又有水平向风压力，即排架计算的第二种情况，由前面计算成果已知，由排架传给基础底板的荷重为：

底板自重及底板以上的回填土重，作均布荷载q

式中：γ混为25kN/m3；γ土为18kN/m3；h2 为底板厚度，h2=0.4m；h4 为回填土高度，h4=1.5m。

3.柱下底板的抗冲切验算

基础底板下部厚度h2=0.4m，沿柱边基础底板不被柱子冲切破坏的条件（忽略杯口周围的剪应力作用，偏于安全）：

式中：Ka 为混凝土达到抗拉极限强度时的安全系数，Ⅳ级建筑物，特殊荷载作用下取Ka=2.0；Rcp为混凝土抗纯剪强度，一般取Rcp=2×15=30kg/cm2；N为由排架传给基础板的轴向力。

= 38.7cm，满足要求。

4.地基反力计算

由图4-61知，地基反力表达式为：

式中：

5.底板内力计算

（1）长边方向。满槽水加上横向风荷载情况对底板受力最不利。在此条件下，计算底板端部的最大和最小地基反力强度σmax和σmin，然后按下式计算底板右边悬臂段，跨中段及左边悬臂段的弯矩M1x，M2x，M3x。

x ≤c 时，

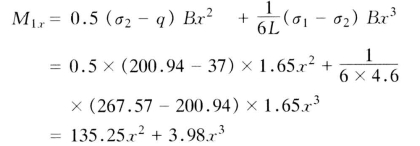
c＜x ≤L -c 时，

x ≥L -c 时，

将x= 0.75代入前两式中，分别得N1 作用截面两侧的弯矩M1= 77.76 kN，M2=100.20kN

将x =L-c = 3.85 代入后两式中，分别得N2 作用截面两侧的弯矩M2=82.65 kN，M3= 105.10 kN。

最小弯矩产生在跨中剪力为零的断面，对M2x求导得：

得

代入式M2x得：Mmin= -299.41 kN·m

（2）短边方向。把基础突出的部分作为固定在柱边截面的悬臂板计算。悬臂板承受的是地基反力，为

则沿短边方向力为q= 234.26×4.6 = 1077.57 kN/m

板端

6.底板配筋

底板配筋可按受弯构件进行配筋，需按长边和短边分别进行配筋。

（1）长边方向。

1）对于柱脚处底板截面：

M =105.10 kN·m，b×h = 600×800 ，取a = 50 mm ，h0 =750mm

所以

底板底面已配筋6Φ20 ，As=1885 mm2，满足要求。

2）对于基础跨中截面按M = 299.41kN 配筋：

基础跨中纵梁已配筋8Φ20，As=2513 mm2，满足要求。

（2）短边方向。

M =303kN·m；b×h = 1650×800 ；取a = 50mm ，h0= 750mm；

已选配16Φ16，As=3218 mm2，满足要求。