两立体相交称为相贯，相贯时形成的表面交线称为相贯线。根据相贯体表面几何形状的不同，可分为两平面立体相交[图4-22（a）]、平面立体与曲面立体相交[图4-22（b）]、两曲面立体相交[图4-22（c）]三种情况。
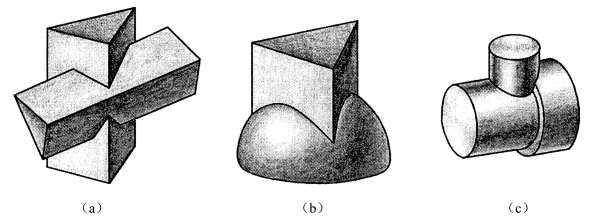
图4-22 两立体相交
在两个立体中，只要有一个为平面立体时，其交线求法可按照截交线方法来求。本节主要讨论两曲面立体相贯时相贯线的性质和作图方法。
由于相交的两曲面立体的形状、大小和相对位置不同，相贯线的形状也不同，但相贯线均具有以下基本性质：
（1）封闭性：由于立体的表面是封闭的，因此相贯线一般是封闭的空间曲线。
（2）共有性：两曲面立体的相贯线是两曲面立体表面的共有线，也是两相交曲面立体的分界线。相贯线上所有点一定是两曲面立体表面的共有点。因此，求相贯线的问题实质上是求线面交点或面面交线的问题。
一、求两曲面立体的相贯线
求作相贯线的方法有三种：积聚性法、辅助平面法和辅助球面法。下面分别介绍。
1.利用积聚性投影求相贯线
当参与相贯的两立体表面的某一投影具有积聚性时，相贯线的一个投影必积聚在这个投影上，因此，相贯线的其余投影便可通过投影关系或采用在立体表面上取点的方法得出。
图4-23所示为两圆柱轴线垂直相交的情况。由于两圆柱轴线垂直相交，且直立圆柱的水平投影有积聚性，水平圆柱的侧面投影有积聚性，相贯线的水平投影和侧面投影分别落在这两个有积聚性的圆上，因此，根据这两个已知的投影，便可按投影关系直接求出相贯线的正面投影。具体作图步骤如下：
（1）求特殊点：A、B点是铅垂圆柱面最左和最右素线与水平圆柱面的交点，它们既是相贯线上的最左、最右点，同时也是最高点。C、D点是铅垂圆柱面最前、最后素线与水平圆柱面的交点，它们既是相贯线上的最前、最后点，同时也是最低点。以上四点的水平及侧面投影可直接做出，再根据投影规律可做出其正面投影。
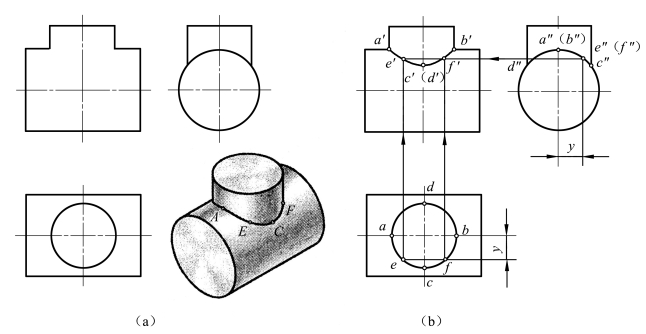
图4-23 圆柱正交相贯
（2）求一般点 由于两圆柱垂直相交，可只求相贯线的前面部分。在相贯线水平投影的适当位置选取左、右对称的两个点E、F的水平投影e、f，求出该两点的侧面投影e″、f″，再求出正面投影e′、f′。
（3）顺序连接各点的正面投影，即得相贯线的正面投影。
两圆柱正交在工程中最为常见，它的交线的产生和形状必须十分熟悉。见表4-3。
从图4-24中可以看出：无论是实心圆柱相交，还是圆柱穿孔或两圆柱孔相交，其交线的形状和画法都是完全相同的。
【例8】图4-25为两圆柱轴线偏交，求其相贯线。
分析：图中所示两圆柱轴线交叉垂直，轴线分别垂直于H面和W面，两圆柱体的相贯线是一条封闭的空间曲线，左右对称。相贯线的水平投影重影在直立圆柱的水平投影上；相贯线的侧面投影重影在水平圆柱的侧面投影上，只需求出相贯线的正面投影即可。
作图：
1）作特殊点：在相贯线的水平投影上选取a、b、c、d、e、f六个点。e、f为水平半圆柱的正面转向轮廓线（最高素线）与直立圆柱面交点的水平投影；a、c、b、d为直立圆柱的最左、最前、最右、最后素线与半圆柱面交点的水平投影；这六个点的侧面投影可直接做出，然后根据投影规律可做出其正面投影。
2）作一般点：在相贯线的水平投影的适当位置选取g、h两点，根据投影规律做出侧面投影g″、（h″），由g″、（h″）、g、h得到g′、h′。
表4-3 两圆柱正交相贯的三种基本形式
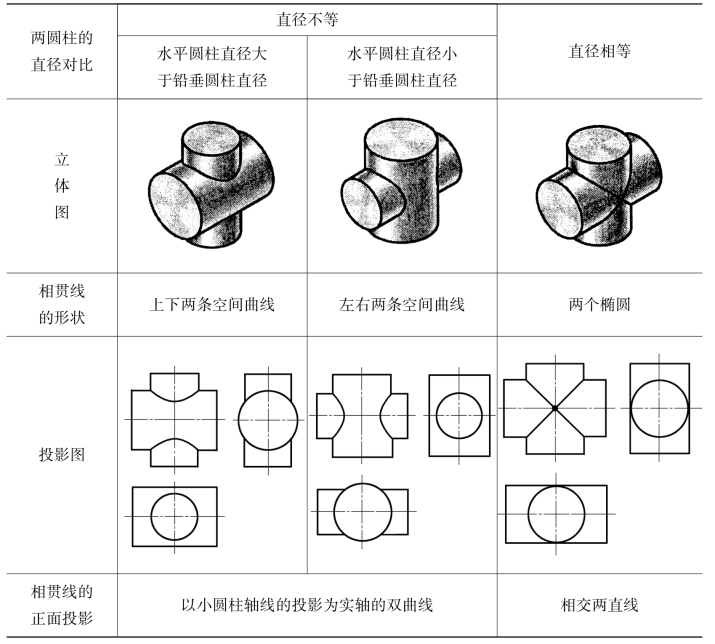(www.xing528.com)
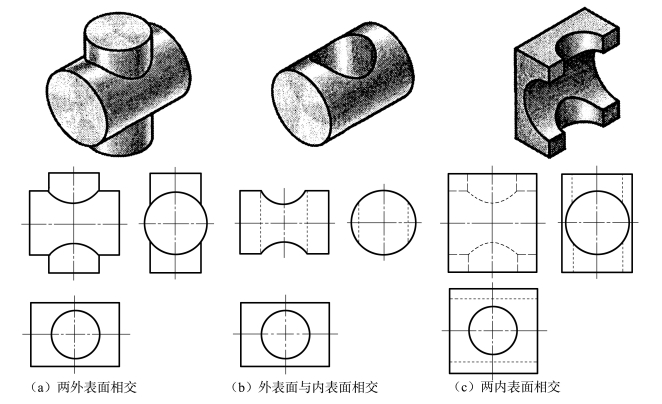
图4-24 圆柱表面相交的三种情况
3）判别可见性并光滑连接各点：A、B两点是直立圆柱正面转向轮廓线上的点，因此这两点为相贯线正面投影可见与不可见的分界点。用粗实线光滑连接a′、g′、c′、h′、b′，用虚线连接a′、（e′）、（d′）、（f′）、b′。由于直立圆柱在水平圆柱之前，所以水平圆柱正面投影轮廓线被挡部分为不可见，应画成虚线。
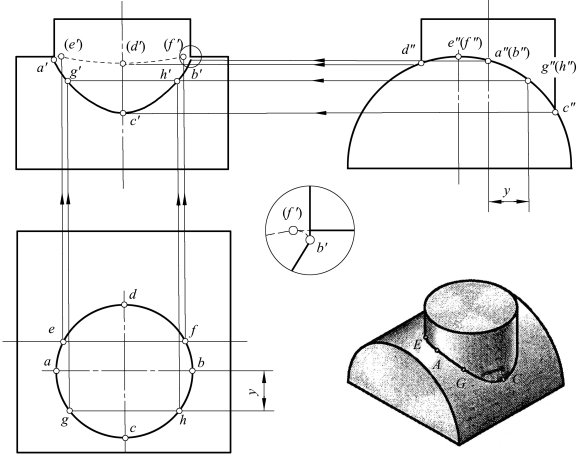
图4-25 两圆柱偏交的相贯线
为了清晰地表示相贯线和轮廓线的连接关系，特采用局部放大图画出，如图4-25中所示的（f′）至b′点。
2.利用辅助平面法求相贯线
利用辅助平面法求画相贯线，其基本方法是利用三面共点原理，如图4-26（a）所示。
选择辅助平面的原则是：使辅助平面与两相贯体的交线的投影为最简单的形式（如圆、直线等）。若相贯体是圆柱，则辅助平面应与圆柱轴线平行或垂直，若相贯体是圆锥，则辅助平面应垂直于锥轴或通过锥顶，相贯体为圆球时，只能选择投影面的平行面为辅助平面。
图4-26为圆柱与圆锥正交的情况。因圆柱的轴线为侧垂线，圆柱的侧面投影积聚为圆，相贯线的侧面投影积聚在这个圆上。相贯线的正面投影和水平投影可用辅助平面法求得。辅助平面可选用水平面或通过锥顶且与圆柱轴线平行的侧垂面。具体作图步骤如下：
（1）求特殊点：由于圆柱、圆锥两轴线相交且平行于正面，故正面投影中两形体轮廓线的交点a′、b′是相贯线上的最高、最低点的投影。B点也是相贯线的最左点。
侧面投影c″、d″是相贯线的最前、最后点的侧面投影。过c″、d″作辅助平面P，平面P截圆锥为圆，截圆柱为两直线，可求得水平投影c、d和正面投影c′、（d′）。C、D两点位于圆柱水平投影轮廓线上，因此，c、d两点是相贯线水平投影可见性的分界点。
在侧面投影中，过锥顶s″作两条与圆柱面相切的素线，它们与圆柱的切点e″、f″是相贯线的最右点的侧面投影。根据点的投影规律可求得其水平投影e、f和正面投影e′、（f′），如图4-26（b）所示。
（2）求一般点：如图4-26（c）所示，在适当位置作一水平辅助面R，R与圆柱相交为两条素线，R与圆锥相交为圆，两者相交于g、h点，即为相贯线上的点，同理，还可求得相贯线上一般点（k）、（j）。
（3）判别可见性并光滑连接各点：由于相贯线前后对称，故相贯线正面投影前后重合，连成实线。在水平投影中，相贯线在圆柱上半部的c、e、g、a、h、f、d点是可见的，连成实线，其余各点在圆柱下半部是不可见的，连成虚线。圆柱水平投影轮廓线应画到c、d两点为止，如图4-26（d）所示。
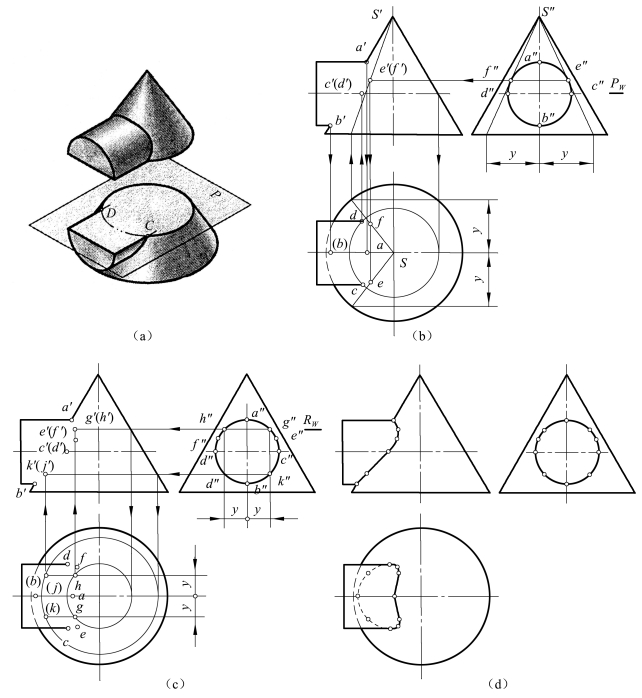
图4-26 圆柱与圆锥正交相贯
二、相贯线的特殊情况
两曲面立体相交，一般情况下相贯线为空间曲线，但在某些特殊情况下，可能是平面曲线或直线。下面介绍两种常见的相贯线的特殊情况。
同轴回转体相交，其相贯线为垂直于回转体轴线的圆。当轴线平行于某投影面时，相贯线在该投影面上的投影为垂直于轴线的直线段。如图4-27所示。
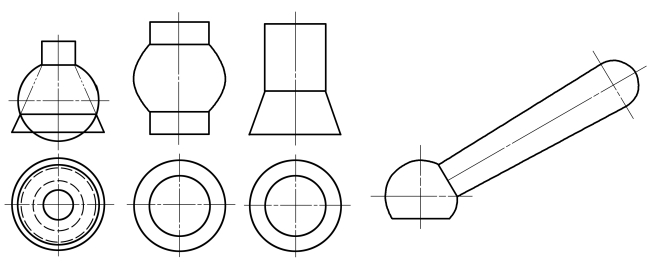
图4-27 同轴回转体的相贯线
两圆柱轴线平行或两圆锥共顶点时，其相贯线是直线，如图4-28所示。
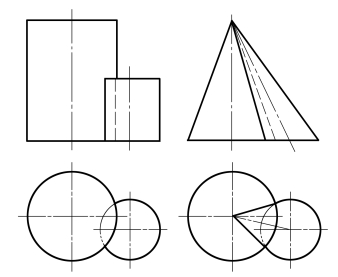
图4-28 相贯线为直线
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
