一、三面投影与三视图
在画法几何学中,几何元素在V、H和W三面投影体系中的投影称为几何元素的三面投影。在机械制图中,国家标准《机械制图》是将机件向投影面投射所得的图形称为视图。所以,投影面上的投影与视图在本质上是相同的。机件在三个基本投影面上所得的三视图分别称为:
主视图——由前向后投射,在V面上所得的视图。
俯视图——由上向下投射,在H面上所得的视图。
左视图——由左向右投射,在W面上所得的视图。
三投影面展开后,机件的三视图如图4-1(b)所示。投影轴由于只反映物体对投影面的距离,对视图之间的投影关系并无影响,故省略不画。
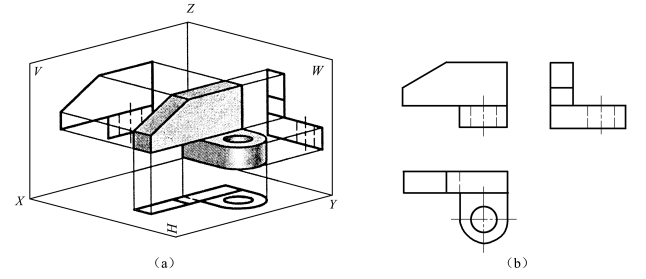
图4-1 立体的三视图
在画三视图时,虽取消投影轴和投影间的连线,但三视图间的各投影仍应保持一定的位置关系和投影规律,俯视图在主视图的下方,左视图在主视图的右方,如图4-2所示。按照这种位置配置视图时,国家标准规定一律不标注视图的名称。
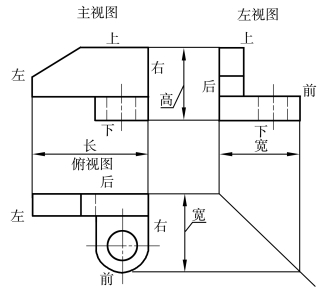
图4-2 三视图的位置关系和投影规律
对照图4-1和图4-2可以看出:
主视图反映了物体上下左右的位置关系,即反映了物体的高度和长度以及物体前面的形状。
俯视图反映了物体左右前后的位置关系,即反映了物体的长度和宽度以及物体上面的形状。
左视图反映了物体上下前后的位置关系,即反映了物体的高度和宽度以及物体左面的形状。
由此可得出三视图之间的投影规律为:
主、俯视图长对正;主、左视图高平齐;俯、左视图宽相等。
“长对正、高平齐、宽相等”是画图和看图必须遵循的最基本的投影规律,不仅适用于整个物体的投影,也适用于物体的每个局部的投影。在应用这一投影规律画图和看图时,必须注意物体上、下、左、右、前、后六个部位与视图的关系,如图4-2所示。如在俯视图和左视图中,靠近主视图的一边都反映物体的后面,远离主视图的一边则反映物体的前面。因此,在根据“宽相等”作图时,不但要注意量取尺寸的起点,而且要注意量取尺寸的方向。
二、平面立体
表面均为平面的立体称为平面立体,平面立体上相邻两表面的交线称为棱线。常见的平面立体有棱柱和棱锥。
1.棱柱
棱柱的上、下底面是互相平行且全等的多边形。除属于上、下底面的棱线外,其侧棱线都互相平行。按侧棱线的数目分为三棱柱、四棱柱……。侧棱线与底面垂直的称作直棱柱,上、下底面均为正n边形的直棱柱又称为正n棱柱。
(1)棱柱的投影:图4-3为一正六棱柱,顶面和底面为水平面,其水平投影反映正六边形的实形,六个棱面中前后面为正平面,其余为铅垂面。它们的水平投影都积聚成直线与六边形的边重合。六条侧棱线是六条铅垂线,其水平投影积聚在正六边形的六个顶点上,其正面投影和侧面投影均反映实长。
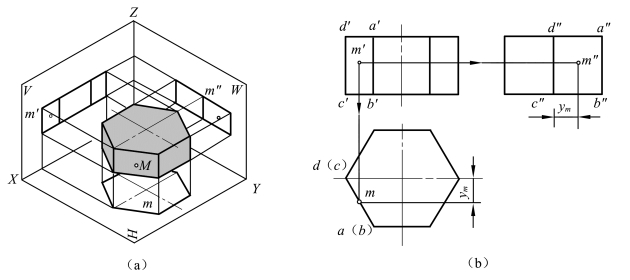
图4-3 正六棱柱的投影及表面上取点
作图时,可先画出正六棱柱的有积聚性的投影正六边形,然后按投影关系,完成其他两面投影。
在视图图形对称时应画出对称中心线,中心线用点画线表示,画法如图4-3(b)所示。
(2)棱柱表面上取点:在平面立体表面上取点,其原理和方法与平面上取点相同。
在图4-3中,由于棱柱表面都处在特殊位置,所以棱柱表面上点的投影均可利用平面投影的积聚性来作图。在判断可见性时,若该平面处于可见位置,则该面上点的同面投影也可见,反之为不可见。有积聚投影的平面上的点的投影,不必判断其可见性。
如图4-3(b)所示,已知六棱柱表面上M点的正面投影m′,求出其他两投影m、m″。
由于点M所属棱面ABCD为铅垂面,其水平投影有积聚性,因此,点M的水平投影m必在该棱面积聚性投影abcd上,根据m′、m求出m″,由于ABCD的侧面投影为可见,故m″也为可见。
2.棱锥
(1)棱锥的投影:棱锥是由一个多边形底面和若干个共顶点的三角形棱面所围成的。从棱锥顶点到底面的距离叫作棱锥的高。当棱锥底面为正多边形,各棱面是全等的等腰三角形时,称之为正棱锥。
图4-4所示为一正三棱锥,其顶点为S,棱锥底面为正三角形ABC,且平行于H面,其水平投影△abc反映实形,正面投影和侧面投影分别积聚为直线段。棱面SAC为侧垂面,其侧面投影积聚为一直线段,水平投影和正面投影仍为三角形。棱面SAB和SBC均为一般位置平面,它们的三面投影均为三角形。棱线SB为侧平线,SA、SC为一般位置直线;底棱AC为侧垂线,AB、BC为水平线。其投影可根据不同位置直线的投影性质进行分析。
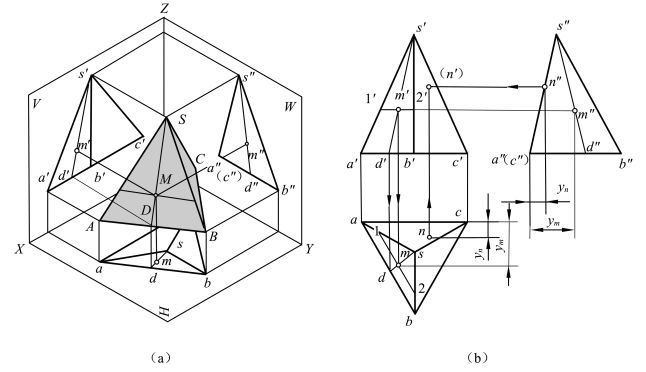
图4-4 正三棱锥的投影及表面上取点
作图时,先画出底面△ABC的各个投影,再做出锥顶S的各个投影,然后连接各棱线即可。三棱锥的三面投影中,除棱线s″(c″)与棱线s″a″重合之外,其余各棱线的投影都可见。
(2)棱锥表面上取点:如图4-4(b)所示,正三棱锥表面上有一点M,已知它的正面投影m′,求作另外两个投影。由于m′是可见的,可知点M属于棱面SAB,可过点M在△SAB内作一直线SD,即过m′作s′d′,再做出sd和s″d″,也可以过点M在△SAB内作平行于AB的直线12,同样可以求得点M的另外两个投影。
又已知棱锥表面上点N的水平投影n,且点N属于棱面SAC,因此,可以由水平投影直接求得侧面投影n″,再由n和n″求得点N的正面投影(n′)。
三、曲面立体(https://www.xing528.com)
曲面立体是由曲面或曲面和平面围成的。常见的曲面立体有圆柱、圆锥、圆球和圆环。这些曲面都是由母线(直线或圆)绕某一轴线旋转而成的,所以又称回转体。回转面上任一位置的母线称为素线。
1.圆柱
圆柱是由圆柱面和上、下底面所围成。底面为圆,圆柱面可以看成是由一直线绕与之平行的轴线回转一周而成,其素线都平行于轴线。
(1)圆柱的投影:如图4-5所示,圆柱的轴线垂直于水平面,顶面和底面均为水平面,故水平投影反映实形;圆柱面的水平投影积聚为一个圆周,圆柱面上任何点和线的投影都积聚在该圆周上。正面投影中,上下两外形线分别是圆柱的顶面和底面有积聚性的投影,左右两外形线分别是圆柱面上最左、最右两条素线(前后分界的转向轮廓线)的投影,最左、最右素线在水平投影中均积聚成一点,而在侧面投影中都重合在圆柱轴线的投影上。侧面投影中,两外形线分别为圆柱的最后、最前素线(左右分界的转向轮廓线)的投影。
关于可见性的判别:在正面投影中,前半圆柱面是可见的;在侧面投影中,左半圆柱面是可见的。
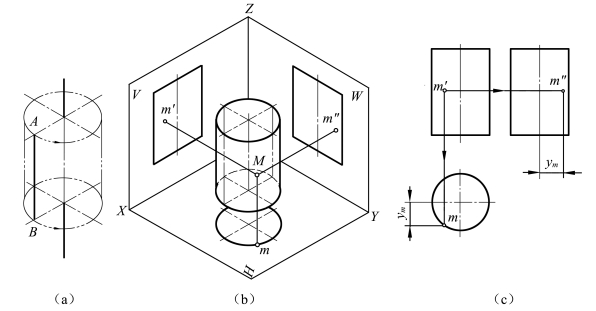
图4-5 圆柱的投影及表面上取点
(2)圆柱表面上取点:当圆柱面的回转轴线垂直于某一投影面时,则圆柱面在该投影面上的投影具有积聚性,利用这一投影性质,在圆柱面上取点、取线的作图比较简便。如图4-5(b)所示,已知圆柱表面上点M的正面投影m′,求m和m″。由于m′是可见的,因此点M必定在前半个圆柱面上。其水平投影m在圆柱具有积聚性的水平投影圆的前半个圆周上,由m′和m可求出m″。因点M在圆柱的左半部,故m″可见。
2.圆锥
圆锥体由圆锥面和底面围成。底面为圆,圆锥面由直线绕与它相交的轴线回转一周而成,因此,圆锥面的素线都是通过锥顶的直线。
(1)圆锥的投影:如图4-6所示,圆锥的轴线垂直于水平投影面,其水平投影为一圆,此圆既是整个圆锥面的水平投影,同时也是圆锥底面的投影。圆锥的正面投影和侧面投影是形状和大小相同的等腰三角形。等腰三角形的底是圆锥底圆的投影;三角形的两个腰是一对投影面的转向轮廓线。在正面投影中是最左、最右素线的投影,在侧面投影中是最前、最后素线的投影。
关于可见性的判别:在正面投影中,前半圆锥面可见;在侧面投影中,左半圆锥面可见;在水平投影中,圆锥面都是可见的。
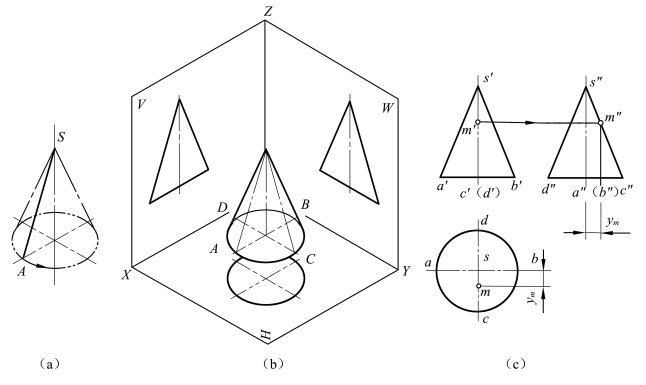
图4-6 圆锥的投影
(2)圆锥表面上取点:由于圆锥面的投影没有积聚性,故在圆锥面上取点必须通过在圆锥面上作辅助线的方法求解。方法有两种,即素线法和纬圆法。
【例1】已知圆锥面上点K的正面投影k′,求作点K的水平投影k和侧面投影k″。
解:
1)素线法:如图4-7所示,过锥顶S和点K作一素线SG,做出其正面投影s′g′和水平投影sg,就可求出K点的水平投影k,然后由k′、k求得(k″)(K点在圆锥的前右半部,所以k可见,k″不可见)。
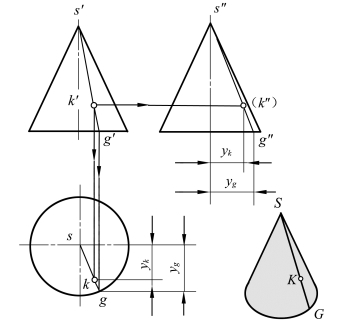
图4-7 素线法求圆锥面上点的投影
2)纬圆法:如图4-8所示,过点K在圆锥面上作一与轴线垂直的水平辅助圆。该圆的正面投影为过k′且垂直于轴线的直线段,它的水平投影为与底圆同心的圆,k必在此圆周上,由k′可求出k,再由k′和k求得(k″)。
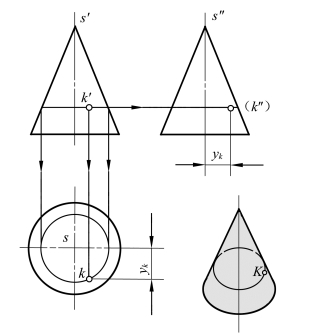
图4-8 纬圆法求圆锥面上点的投影
3.圆球
圆球是由球面围成的。球面可以看成是一圆母线绕其直径回转180°而成。
(1)圆球的投影:如图4-9所示,圆球的三个投影都是与球的直径相等的圆,它们分别是球面对三个投影面的转向轮廓线。球的转向轮廓线是平行于相应投影面的最大的圆,也是两半球面的分界线。
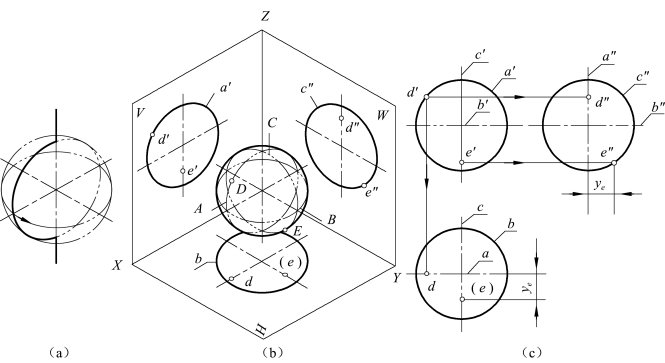
图4-9 圆球的投影
球的正面投影圆是球面上平行于V面的最大圆A的投影,它的水平投影a积聚成一直线并与水平中心线重合;侧面投影a″与相应圆的铅垂中心线重合。正面投影圆把球面分成前、后两部分,前半球正面投影为可见,后半球正面投影为不可见,它是正面投影可见面与不可见面的分界线。球的水平投影圆是球面上平行于H面的最大圆B的投影;球的侧面投影圆是球面上平行于W面的最大圆C的投影。球心的投影是各个投影图中对称中心线的交点。作图时,可先确定球心的三面投影,再画出三个与圆球等直径的圆。
(2)圆球表面上取点:球面的三个投影都没有积聚性,且球面上也不存在直线。因此,在球面上取点,只能采用过该点作与投影面平行的辅助圆的方法。
如图4-10所示,已知圆球表面上一点M的正面投影m′,求其水平投影m和侧面投影m″。根据m′的位置和可见性,可知M点位于前半球的左上部位。可过点M作一平行于水平面的辅助圆,在水平面上的投影反映该圆实形。m必在该圆上,由m′可求得m,再由m′和m而获得m″,m、m″均为可见。也可以过点M作平行于正面或平行于侧面的辅助圆来作图,请读者自行分析。
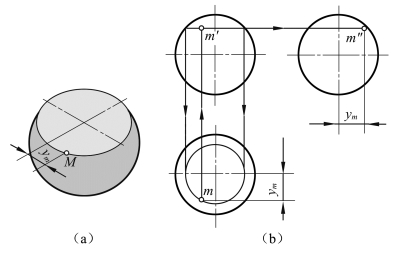
图4-10 圆球表面上取点
4.圆环
圆环是由环面围成的。环面可以看成是一圆母线绕和它共面但不过圆心的轴线旋转一周而成。靠近轴的半个环面为内环面,远离轴的半个环面为外环面。
(1)圆环的投影:如图4-11所示,圆环轴线垂直于水平投影面。正面投影上的左、右两圆是圆环上平行于正投影面的A、B两素线圆的投影;侧面投影上的两圆是圆环上平行于侧投影面的C、D两素线圆的投影;正面和侧面投影上顶、底两直线是环面最高、最底圆的投影;水平投影上画出了最大和最小圆以及中心圆的投影。
(2)圆环表面上取点:如图4-11(c)所示,已知圆环面上点M的正面投影m′,求m和m″。可过点M作平行于水平面的辅助圆来求得,该圆的正面投影为过m′且平行于X轴的水平线段1′2′,水平投影为直径等于12的圆,m必在此圆上,由m′可求得m,再由m′、m求得m″。
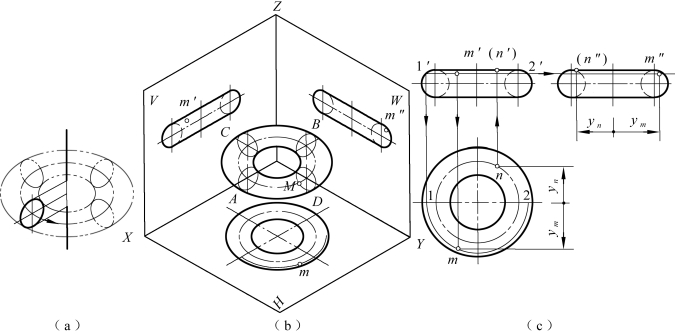
图4-11 圆环的投影及表面上取点
N点在圆环面的最高圆上,已知N点的水平投影n,求作其正面投影及侧面投影。利用点的投影规律可直接做出(n′)和(n″)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




