点的投影及重影点分析

一、点在三投影面体系中的投影

1.三投影面体系的建立

如图3-5（a）所示，三个投影面互相垂直相交，其交线OX、OY、OZ称为投影轴，三个投影轴的交点O称为原点。

2.点的三面投影图

如图3-5（a）所示，空间点A分别向H、V、W面作垂线，所得垂足a、a′及a″即为A点的水平投影、正面投影和侧面投影。

将三投影面体系展开，即V面不动，H面绕OX轴按图示箭头方向向下旋转90°与V面重合，W面绕OZ轴按图示方向向右旋转90°与V面重合，去掉边框，即得点A的三面投影图，如图3-5（c）所示。其中OY轴随H面旋转时记作OYH，随W面旋转时记作OYW，但都表示同一OY轴。

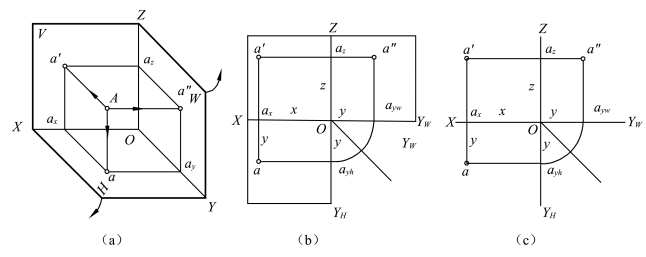
图3-5　点在三投影面体系中的投影

3.点的三面投影与坐标的关系

如果把三投影面体系看作空间直角坐标系，则H、V、W面即为坐标面，OX、OY、OZ即为坐标轴，O点即为坐标原点，而点到W、V、H投影面的距离可以直接用坐标x、y、z表示。参照点在两投影面体系中的投影分析可知，图3-5（a）中点A（xA，yA，zA）的坐标与该点的投影关系如下：

A点的水平投影a由xA、yA两坐标确定，正面投影a′由xA、zA两坐标确定，侧面投影a″由yA、zA两坐标确定。点的任何两个投影均可反映该点的三个坐标，即可确定该点的空间位置。如果已知空间点的三个坐标或它的两个投影，就可以根据点的投影规律做出它的三面投影图。这是补视图、补缺线的重要理论依据。

4.点的三面投影规律

三投影面体系中点的投影规律如下：

（1）点的正面投影和水平投影的连线垂直于OX轴，这两个投影共同反映空间点的x（横）坐标，即

（2）点的正面投影和侧面投影的连线垂直于OZ轴，这两个投影共同反映空间点的z（高）坐标，即

（3）点的水平投影到OX轴的距离等于侧面投影到OZ轴的距离，这两个投影共同反映空间点的y（纵）坐标，即

(www.xing528.com)

根据点的三面投影规律，可由点的三个坐标值画出三面投影图；也可根据点的两个投影做出第三投影。

【例1】已知A点的坐标（20，15，10），B点的坐标（30，10，0），C点的坐标（15，0，0），做出点的三面投影图，如图3-6（a）。

分析：由于zB=0，B点在H面上，又由于yC=0，zC=0，C点在X轴上。

作图：A点的投影：从O点向左在X轴20处作垂线aa′，然后在aa′上从OX轴向下向上分别取yA=15和zA=10，做出a和a′，由a′作OZ轴的垂线，然后从OZ轴向右方取15即得a″。

其他从略。

【例2】已知D点的两个投影d′、d″，求出其第三投影d，如图3-6（b）。

分析：由于已知点的正面投影d′和侧面投影d″，则点的空间位置可以确定，由此可以做出其水平投影。

作图：根据点的投影规律，水平投影d到OX轴的距离等于侧面投影d″到OZ轴的距离。先从原点O作YH、YW分角线，然后从d″引OYW轴的垂线与分角线相交，再由交点作OX轴的平行线与由d′做出的OX轴的垂直线相交即得水平投影d。

【例3】已知点A的三面投影画出其轴测图，如图3-6（c）。

分析：根据A点的三面投影图，即可确定A点的三个坐标（xA，yA，zA），然后按坐标值作图。

作图：通常将轴测图上的OX轴画成水平位置，OZ轴画成铅垂位置，OY轴画成与OX、OZ轴成135°，即与OX轴延长线成45°。在相应轴上量取坐标xA、yA、zA，得到ax、ay、az三点，然后从这三点分别作各轴的平行线得三个交点，即为a、a′、a″，再从a、a′、a″作各轴的平行线相交于一点，即得空间点A。

二、两点的相对位置和重影点

空间两点的相对位置可由两点的坐标差来确定。x坐标大者在左，y坐标大者在前，z坐标大者在上。以图3-7所示A、B两点为例：

xA＜xB则点A在点B之右；yA＜yB则点A在点B之后；zA＞zB则点A在点B之上。

图3-6　点的投影作图

图3-7　两点的相对位置及重影点

重影点：

若空间两点有两个坐标对应相等时，该两点将处于某一投影面的同一条投射线上，因而在该投影面上具有重合的投影，此两点称为该投影面的重影点。如图3-7所示，A、C两点位于对H面的同一条投射线上，它们的水平投影重合，因zA＞zC，从上往下看时，A点可见，C点不可见。在投影图上，对不可见点的投影加括号表示，如a（c）。