对于服装纸样而言,其结构的几何形状根据款式造型的需要是多样的,但其纸样的几何形状是由几何元素按一定的连接关系组合而成的。这些几何元素的数学基础、计算和分析以及它们的相互关系是几何数据处理的对象。它们在二维图形上一般用点、直线、曲线来表示,所以在服装纸样参数化设计中,最常用的二维参数化图形表示中涉及的基本元素主要是点、直线和曲线。
(一)点
通常情况下,平面上的一个点P由它的一对坐标值定义,如用P(x,y)表示二维平面中的一个点,如图4-5所示。
(二)直线
已知二维空间中的两点P1(x1,y1)及P2(x2,y2),如图4-6所示。引入参数λ,则直线的参数方程可表示为:
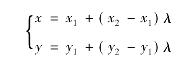
λ∈(-∞,+∞)时,方程表示过P1与P2点的无限长的直线。
若λ∈[0,1],则表示两端点为P1和P2的直线,点P(x,y)必定位于两端点之间。
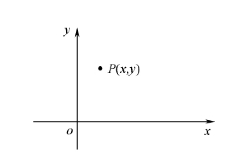
图4-5 点的描述
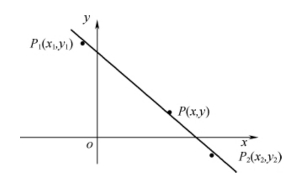
图4-6 直线
(三)圆弧曲线
圆弧曲线是服装纸样设计的常用曲线,如图4-7所示。圆弧曲线的参数方程可表示为:
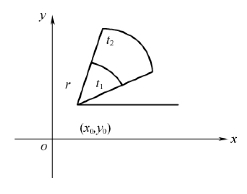
图4-7 圆弧曲线
![]()
式中:r——圆弧半径;
(x0,y0)——圆心坐标;
t1,t2——分别为起始角和终止角。
当参数t以d t为步距变化时,利用圆弧的参数表达式可计算出圆弧上的点,把这些点依次用直线连接起来,可得到圆弧的近似曲线。
(四)自由成形几何元素
在服装制板中,除了直线和圆弧之外,还有许多不规则自由曲线。自由曲线设计的工作量特别大,这些自由曲线的设计相对于直线、圆和圆弧也比较复杂。如袖窿弧线、领圈弧线等,这类曲线在手工制板中,是定长取点,再光滑连接,称为画顺,即曲线的边接要光滑。这时光顺的质量完全取决于打板师的技术,但在计算机打板时,任何不规则曲线必须严格按数学方法描述。因此自由曲线的算法问题是服装CAD系统设计的关键。目前在服装设计和造型中较多地采用三次样条曲线、二阶或三阶Bezier曲线以及B样条曲线。
1.自由成形几何元素生成的方法
在纸样设计中,通常用一组离散的型值点来定义和构造几何图形。这种定义曲线的方法有插值、逼近或拟合三种。
(1)插值。给定一组精确的数据点,要求构造一个函数,使之严格地依次通过全部型值点,且满足光顺要求,如图4-8(a)所示。
(2)拟合。给定一组具有误差的数据点,构造一个函数,使之在整体上最接近这些数据点,不必通过全部数据点使之构造的函数与所有数据点的误差在某种意义上最小,如图4-8(b)所示。
(3)逼近。逼近是用特征多边形或网络来定义和控制曲线的方法,如图4-8(c)所示。
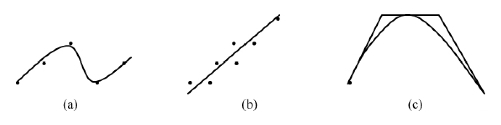
图4-8 自由成形不规则曲线生成的方法
2.三次样条(Sp llne)曲线
在样条曲线中,分段三次样条曲线在连接处达到二阶连续的最低次的曲线,便于计算,因此在服装纸样设计中得到广泛应用。而且三次样条曲线的数学表达式简单,计算方便,且性能稳定,便于分析。参数表示方法还有许多优点,如曲线的方程与坐标系的选择无关,化多值函数为单值函数等。三次样条曲线中由于每个控制点都在曲线上,改变任何一个控制点只对曲线的局部形状产生影响,因此在纸样设计中可用之为局部曲线造型。
设有离散点p0(x0,y0)、p1(x1,y1)、Lpn(xn,yn),若有一条曲线p(t)满足:
(1)顺次经过点pi(i=0,1,L,n)。
(2)在每两个点pi、pi+1(i=0,1,L,n-1)之间是三次参数曲线。
(3)整段曲线是二阶连续的。
则称曲线p(t)为三次参数样条曲线,如图4-9所示,其曲线方程为:(https://www.xing528.com)
p(t)=∑Bi(t)ti-1 (i=1,2,L,4)
3.贝赛尔(Bezier)曲线
在外形设计中,样条曲线作为外形设计工具还缺少灵活性和直观性。针对这些问题,法国的Bezier提出了一种描述曲线的方法。Bezier曲线的形状是通过一组多边折线唯一确定出来的,该多边折线一般称为Bezier曲线控制多边形或特征多边形(图4-10)。p0,p1,p2,p3各点为Bezier曲线的控制顶点,改变特征多边形的顶点位置,可以改变Bezier曲线的形状。由于只有多边形的第一个顶点和最后一个顶点在曲线上,因此在纸样设计中只要给出首末点,就可绘制出圆顺的曲线。而且改变任何一个控制点的位置都会对整条曲线产生影响,因此它的整体塑型性比较好,在纸样设计中可称之为整体造型曲线。
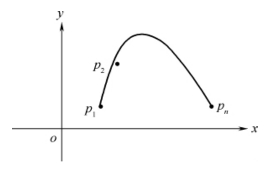
图4-9 三次样条(Spllne)曲线
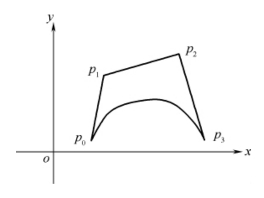
图4-10 贝赛尔(Bezier)曲线
Bezier曲线的数学基础是在起点和终点之间构造的插值多项式混合函数,通常用n+1个顶点定义一个n次多项式。其曲线方程为:
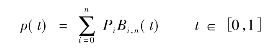
其中,pi是各顶点的位置向量,Bi,n(t)是古典伯恩斯坦多项式,称为基底函数,也是Bezier曲线特征多边各顶点向量的混合函数。
![]()
式中:i=0,1,2,∧,n。
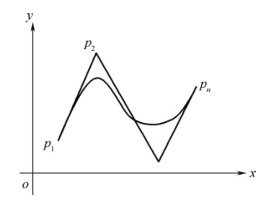
图4-11 B样条(B-spline)曲线
4.B样条(B-spline)曲线
贝赛尔(Bezier)曲线增加或减少曲线阶次的唯一方法是增加或减少控制顶点的数量。B样条曲线是三次样条曲线和Bezier曲线的拓展,B样条曲线的局部修改性好,改变某一控制顶点,仅影响附近一段曲线,如图4-11所示。更重要的是B样条曲线的基函数的次数与控制点的数量无关,使得它能具有较好的圆顺性。B样条(B-spline)曲线的数学表达是:
![]()
若给定m+n+1个空间向量Pk(k=0,1,2,L,m+n),称n次参数曲线为n次B样条的第i段曲线(i=0,1,2,L,m),它的全体称为n次B样条曲线。依次用线段连接pi+l(l=0,1,2,∧,n)中两个相邻两个向量的终点,那么所组成的多边形称为样条在第i段的控制多边形。B样条函数的基函数为:
![]()
式中:l=0,1,2,∧,n。
(五)自由成形不规则曲线的适用性分析
1.三次样条曲线适用性分析
三次参数样条插值曲线是最早应用于CAD/CAM设计的曲线之一,也是在纸样设计中应用很广泛的一种曲线。它的主要特点是算法较简单,易实现,且计算稳定。
三次样条曲线在纸样设计中的应用是依次平滑连接各已知点,如图4-12画袖山曲线,当袖山曲线上各辅助点确定后,用三次样条曲线连接形成袖山曲线。
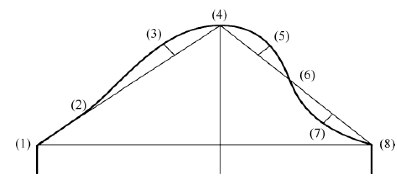
图4-12 三次样条曲线应用
但是,三次参数样条插值曲线不具有局部修改能力,作为设计工具缺少灵活性和直观性,修改任何一个数据点都会引起整条曲线的变化,需要引入控制曲线。这给服装板型的修改带来了一定的困难。
2.Bezier曲线适用性分析
由于Bezier曲线与其控制多边形之间的关系直观、简明,使得曲线的拟合、修改相对容易,同时二阶与三阶Bezier曲线绘制计算量相对小于其他自由曲线。当所有控制点都在曲线一侧时,可用于纸样设计的抹圆处理。如图4-13所示,前领口曲线绘制中,当控制点0、1、2确定之后,可利用Bezier曲线在1点处抹圆,将曲线画顺。当改变控制点时,曲线的形状也发生相应变化。但是,当控制点在曲线两侧时,曲线在中间控制点出现反曲。
Bezier曲线是通过逼近特征多边形而获得的,但控制点的数量控制了曲线的阶次,增加或减少曲线阶次的唯一方法是增加或减少控制点数量。因此,改变任何一个控制点的位置都会对整条Bezier曲线产生影响,需要对其进行拓展,引入B样条曲线。
3.B样条曲线适用性分析
B样条曲线虽然应用时间不算太长,但它拥有成熟的算法,由于B样条曲线采用控制点定义曲线,而进行服装板型拟合时,需要曲线经过所有的关键点,因此,本文中的B样条曲线都采用了反算法使其通过所有的关键点,反算法是根据给定的型值点先计算出曲线控制多边形的顶点,使其定义的曲线通过给定的型值点,B样条曲线是局部逼近,修改控制点的位置对曲线的影响只是局部的,因此B样条曲线具有良好的局部控制能力,使服装板型曲线的局部修改更易控制。
B样条曲线(图4-14)能更好地解决4个以上控制点的逼近问题。可以控制点重合共线的多种情况,特别是纸样设计中的拐角处的设计。例如在腰节处设计圆角时,控制点依次为1、2、3、4、5、6,(3)和(5)点为抹圆辅助点。若设计成方角时,控制点仍然为1、2、3、4、5、6,令3、4、5三点重合,即a=b=0,则在4点处形成角点,完成设计。

图4-13 Bezier曲线应用
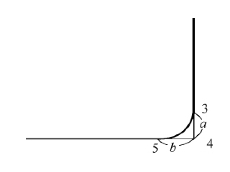
图4-14 B样条曲线应用
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




