约束(Constraint)是描述一组对象所必须满足的某种特定关系的断言。约束是一个应用很广泛的概念,在参数化/变量化建模中约束主要指设计对象在设计空间受到某种限制。设计本质就是一个约束满足问题,设计过程即给定功能、结构、材料及制造等方面的约束,建立一个满足设计要求的约束系统。
约束是特定元素之间必须满足的一组关系。约束满足问题可以通过一个有限集以及作用在这个有限集上的一组关系来定义。在一个约束系统中,对于一个有限的元素集,E={ei∣i=1,…,m},存在一组关系C={Cj∣j=1,…,m},其中要求所有ei满足Cj(e1,…,ei)。CSP的主要任务就是考察是否存在能使每一个ei∈C得到满足的情况。如果存在这样的ei的解,则能够把它找出来。这个解又称作M的一个实例,它是任何满足C的元素集合,获取M的实例是通过对C中变量的赋值实现的。
(一)约束类型
设计本质上是通过提取特征有效的约束来建立其约束模型并进行约束求解。
这些约束一般根据不同的产品特征、产品结构和设计过程的不同来转化,并将这些限制综合成设计目标,然后将它们映射成为特定的几何和拓扑结构,从而转化为约束。参数化建模中的约束类型从宏观上可以分为几何约束与工程约束。几何约束是指构成图形的各个几何元素之间所固有的某种结构与形状关系,如平行、垂直、水平、竖直、相切、同心等。几何约束保证了图形元素改变尺寸后图形能大致保持原来的形状。
在服装纸样设计系统中,如果已经为纸样几何图形的位置大小关系定义了约束,在确定造型逻辑时,参数化系统特性就可以用来携带和保留设计逻辑,只要简单地改变参数就能使纸样发生变化。按照约束的输入方式,约束可分为显示约束和隐式约束。通常,参数约束以显示的形式输入,而拓扑约束则是隐含的。将参数约束和几何约束作为构成几何或拓扑结构的几何要素和轮廓要素,可以导出各形状结构的位置和形状参数,从而形成参数化的几何模型。对于服装CAD系统约束可分为参数约束和几何拓扑约束。参数约束和几何拓扑约束可以统一为一种表示方法,用以下形式表示:
C=(T,01,02,V)
式中:C——约束(constraint);
T——类型(type);
01、02——分别表示约束对象(object);
V——约束值(value)。
1.几何拓扑约束
一个物体的几何和拓扑是紧密联系的,拓扑约束用来约束几何体的结构以及各几何元素的固定联系,包括水平、竖直、平行、垂直、相切、共线、同心七种约束类型。拓扑约束表达了图形元素之间的空间连接关系,是维系图形拓扑结构不变的基本关系,在变量和参数化应用中它都是不变的。拓扑约束关系是隐式的,由系统自动检测出来。
(1)平行约束。
(PAR,L1,L2,1/-1):L1、L2两直线平行。
(2)垂直约束。
(PER,L1,L2,1/-1):L1、L2两直线垂直。
(3)点在直线上。
(ON_L,P,C,1):点在直线L上。
(4)点在圆上。(https://www.xing528.com)
(ON_C,P,C,1):点在圆C上。
(5)线圆相切约束。
(TAN_LC,L,C,1/-1):直线L与圆相切。
2.参数约束
参数约束用来约束各几何元素尺寸的大小,参数约束又分为数值约束和关系式约束。数值约束一般指对可以具体测量的数值进行限制;关系式约束由可变的数值说明和另外的一些参数(如打板规则等)组成,如前肩宽=后肩宽-0.7cm。通常包括七种,即水平约束、竖直约束、两点距离、点到直线距离、点到坐标轴距离、两线夹角约束和直径等。
(1)点与点的距离约束。
(D_PP,P1,P2,d):点P1到P2的距离是d。
(2)点到线的距离约束。
(D_PL,P,L,d/-d):点P到直线L的距离是d/-d。
(3)两直线的角度约束。
(ANG,L1,L2,A):直线L1到直线L2的角度是A。
(二)基于约束的参数化设计的体系结构
1.参数化图形的几何约束模型
参数化技术的实质就是以几何约束系统表示产品的几何模型,并且试图实现产品几何模型的约束驱动,即在确定产品几何约束模型之后,通过给予特定约束值自动地确定产品的几何模型。实际上,可以将产品参数化/变量模型理解为一个对偶的复合模型,这个对偶复合模型由几何模型和约束模型组成,如图4-3所示。
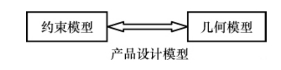
图4-3 对偶复合模型
2.基于约束的参数化设计的体系结构
如图4-4所示,在参数化设计中,用户通过绘制纸样,指定拓扑关系,并标注尺寸定义初始纸样。约束处理器从图形元素结构中提取特征点,构造几何向量,从拓扑约束和尺寸约束中提取约束,系统依据各种约束情况或几何推理结果,为用户提供各种信息,如特征点的运动方向,过或欠约束等。当用户修改尺寸时,约束处理器依据纸样描述的约束信息重新对轮廓进行处理,生成新的纸样。

图4-4 基于约束的参数化设计的体系结构
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




