调幅电路及其优化设计

调幅电路将电容的变化转换为输出电压幅值的变化，它包括交流电桥电路和运算放大器式电路。

1）交流电桥电路

交流电桥电路的供桥电源为交流信号，根据桥路结构的不同可分为：普通电桥、紧耦合电感电桥、变压器电桥、双T二极管交流电桥。

（1）普通交流电桥

普通交流电桥由传感器电容、固定电容及配接阻抗组成，如图3.17所示。由Cx、C0、Z和Z′组成一个交流电桥的测量系统，其中，Cx为电容传感器的电容，C0为固定电容，Z和Z′为等效的匹配阻抗。

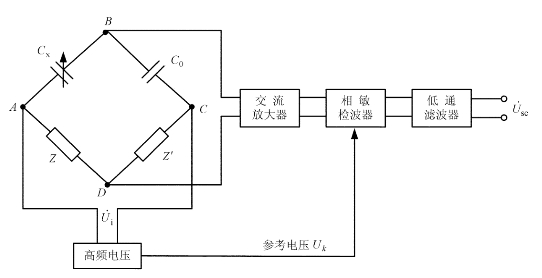
图3.17　普通交流电桥电路结构

在普通交流电桥电路中，由振荡器产生一个等幅高频交流电压，加在交流电桥的AC端，为交流电桥提供电源电压。BD端为交流电桥的电压输出端。交流电桥的输出电压是一个调幅的载波信号，其频率为电源载波频率，而幅度受被测信号的调制。此信号经交流放大器放大和相敏检波后，得到一个与被测信号变化规律相同的电信号，最后经低通滤波器去除残余载波，得到输出电压。

在测量前，先要进行初始调零，使交流电桥处于平衡状态，输出电压为零。测量时传感器电容Cx发生变化，电桥失去平衡而输出电压，得到的输出交流电压的幅值随电容Cx而变化。因此，这种交流电桥实质上是一种调幅电路，它要求供桥电源的幅度和频率都很稳定，并要求电桥放大器的输入阻抗很高，同时，测量系统的动态响应受电桥供桥电源频率的限制，一般要求交流电源的频率为被测信号最高频率的5～10倍。

（2）紧耦合电感电桥

紧耦合电感电桥由传感器电容和两个互为紧耦合的电感臂构成，如图3.18所示。此电桥常用于差动式电容传感器，以差动形式工作的两个电容Cx1和Cx2作为电桥的工作臂，而紧耦合的两个电感L作为固定臂。初始时传感器电容Cx1＝Cx2＝C，为供桥电源电压，为桥路输出电压。这种电桥的特点是有两个互为紧耦合的电感臂，构成电桥的固定臂。为求出两个固定臂的阻抗Z12和Z13，需先对紧耦合电感部分进行讨论，其等效电路如图3.19所示。

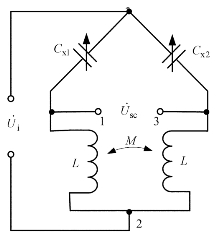
图3.18　紧耦合电感电桥的组成

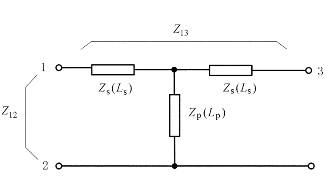
图3.19　紧耦合电感电路的等效图

图3.19中，阻抗Zs的等效电感为Ls，而Zp的等效电感为Lp，根据紧耦合电感有

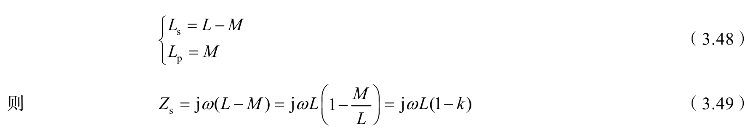
这里，以ω2LC为变量，电桥灵敏度曲线如图3.20所示。由图中可见，电路的谐振点在ω2LC＝1/2处，在谐振点左侧（ω2LC≪1时），灵敏度S与ω2LC成正比，而在谐振点右侧（ω2LC≫1时），灵敏度S趋于2，呈水平特性。因此，为了得到高稳定性，应使ω2LC增大：当ω2LC＞2时，灵敏度S将不随电源频率ω、电感L及传感器电容C的改变而改变。

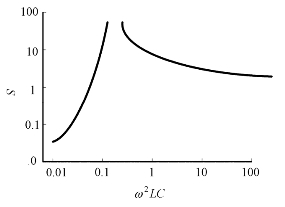
图3.20　紧耦合电感电桥的灵敏度曲线

如图3.21所示，考虑电缆电容C′旁路的影响，因

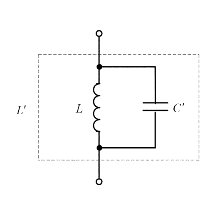
图3.21　考虑电缆电容C′时的等效电感

此时的等效电感L′应为

可见，等效电感L′比L增大了。在实际应用中，可用一个大的固定电容与电感桥臂相并联，以增大等效电感，使ω2L′C≫1，以提高稳定性。

但是等效电感L′增大后，灵敏度S将减小，所以，这种在电感桥臂上并联固定电容的方法，实际上是牺牲灵敏度换取高的稳定性。

（3）变压器电桥电路

变压器电桥电路如图3.22所示，C1和C2为传感器的两个差动电容，构成电桥的工作臂，变压器次级耦合电感为电桥的固定臂，负载阻抗为ZL，输出电压为。

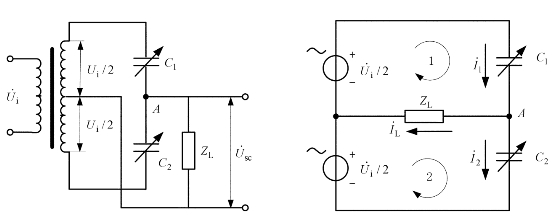
图3.22　变压器电桥电路及简化形式(https://www.xing528.com)

微课：变压器电桥电路

根据基尔霍夫定律列方程组：

所以，将差动式电容传感器接入变压器电桥，在负载阻抗极大时，即使是变间隙型电容传感器，输出电压也与输入位移呈理想的线性关系。

（4）双T二极管交流电桥

如图3.23所示，C1和C2是两个差动工作的电容，也可以一个是传感器电容，另一个为固定平衡电容。D1和D2是两个特性相同的理想二极管，即二极管正向导通时电阻为零，而反向截止时电阻为无穷大。R1和R2为两个固定电阻。这样，由一对二极管、一对电容和一对电阻就构成了双T形的交流电桥。图3.23中，RL为负载电阻，其上输出电压为；为高频电源电压，频率一般为兆赫兹级，提供幅值为U的如图3.24（a）所示的对称方波。

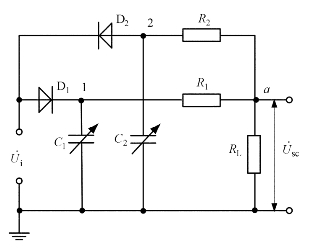
图3.23　双T二极管交流电桥

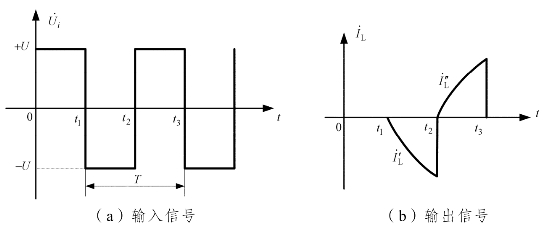
图3.24　双T二极管电桥的输入和输出信号

为便于分析，将图3.23所示双T电路画成图3.25（a）的形式。在t＝0时，为正半周，二极管D1导通，D2截止，C1被迅速充电至＋U，并一直保持到t1时刻，而D2在0～t1时间内一直不导通。

当t＝t1时，转为负半周，则D2导通，C2被迅速充电至-U，而D1突然截止。在t1时刻，由于C1还来不及放电，节点1的电位仍为＋U，而节点2的电位此时为-U，当两个固定电阻R1＝R2＝R时，节点a电位为零，负载电阻RL两端电位差为零，无电流流过，，如图3.25（b）所示。

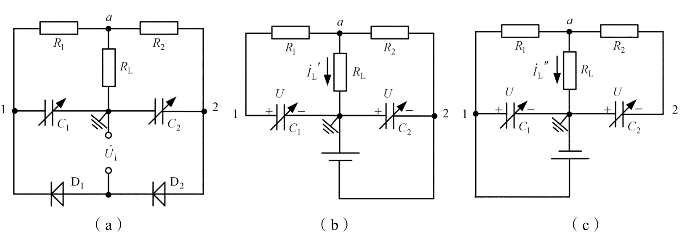
图3.25　双T二极管电桥分析电路

t1时刻后，由于电容C1经R1和RL放电，节点1的电位从＋U按指数规律下降，而节点2的电位在t1～t2期间保持不变，仍为-U，则节点a的电位由零变负，这样，RL上有电流流过，方向由下至上，为负值。由于节点1和节点a的电位均按指数规律变化，也按指数规律变化，如图3.24（b）所示。

当t＝t2时，转为正半周，D1导通，C1被迅速充电至＋U，而D2截止，但C2还来不及放电，于是在t2时刻，节点1的电位为＋U，节点2的电位为-U，节点a的电位为零，此时突变为0，如图3.25（c）所示。

t2时刻后，C2经R2和RL放电，节点2的电位从-U按指数规律上升，而节点1始终为＋U，则节点a的电位由零按指数规律上升，流过RL的电流为正，也按指数规律增大，如图3.24（b）所示。

当C1＝C2，R1＝R2时，由于电容放电的时间常数相同，波形相同，方向相反，则通过RL的电流平均值为零。而当传感器工作时，C1≠C2，则流过RL的电流平均值不为零。C1与C2的差值越大，波形的差别也越大，电流平均值也越大，即输出电压平均值也越大，所以，输出电压平均值反映了电容的变化，也间接反映了被测量的变化。输出电压为

只是电容C1、C2的函数。

微课：运算放大器式电路

2）运算放大器式电路

如图3.26所示，Cx为传感器电容，它跨接在高增益运算放大器的输入端和输出端之间，C0为固定电容，为信号源电压，为输出电压，放大器的开环放大倍数为K。

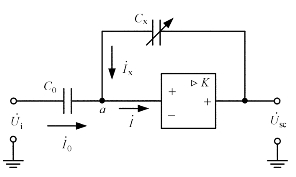
图3.26　运算放大器式电路

由于运算放大器的放大倍数K非常大，而且输入阻抗Zi很高，可作为电容传感器比较理想的测量电路。假设这里的运算放大器是一个高增益的理想放大器，则输入电压Ua近似为零。例如，放大器有±10 V的线性输出，放大倍数为105，则相应的输入为±10－4V，因此可近似认为，称为“虚地”。由于放大器的输入阻抗很高，则放大器的输入电流也近似为零，即。

根据基尔霍夫定律有

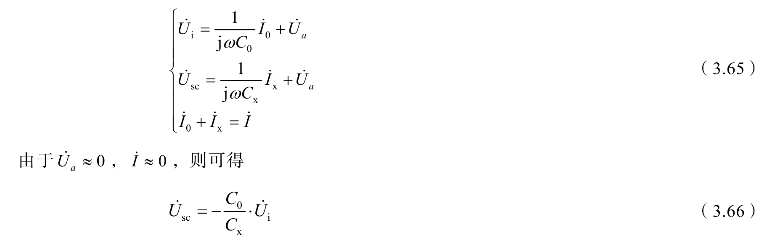
可见，当放大器是一个高增益理想放大器时，电路的输出电压与传感器电容Cx成反比，对变间隙型电容传感器，有

可见，输出与动极板的机械位移δ呈线性关系，这就从原理上解决了单个变间隙型电容传感器输出的非线性问题。式（3.68）是在K→∞，Zi→∞的前提下得到的，而实际运算放大器的K和Zi总是个有限值，所以这种测量电路仍存在一定的非线性误差。但当K、Zi足够大时，这种误差是相当小的，在要求的误差范围之内。