深入探讨传感器动态特性指标

前面介绍了传感器的动态数学模型，它可以用微分方程和传递函数来描述。尽管大多数传感器的动态特性可近似用一阶或二阶系统来描述，但这仅仅是近似的描述而已，实际的传感器往往比简化的数学模型要复杂。因此，传感器的动态响应特性一般并不是直接给出其微分方程或传递函数，而是通过实验给出传感器的动态特性指标，通过这些动态特性指标来反映传感器的动态响应特性。

研究传感器的动态特性主要是为了分析测量时产生动态误差的原因。传感器的动态误差包括两部分：一是输出量达到稳定状态后与理想输出量之间的差别；二是当输入量跃变时，输出量由一个稳态到另一个稳态之间的过渡状态中的误差。研究传感器的动态响应特性，实际上就是分析传感器的这两种动态误差。

要分析动态误差，首先要给出输入量。在实际测试中，输入量总是千变万化的，往往事先并不知道，那么，在这种输入量未知的情况下，如何分析传感器的动态误差，并给出传感器的动态特性指标？在工程上，解决的办法是，选定几种最典型、最简单的输入函数，称为标准信号，将其代入传感器的典型环节中来研究传感器的响应特性。常用的输入标准信号有阶跃函数、正弦函数、指数函数及冲击函数（δ函数）等。其中，阶跃函数和正弦函数在物理上较易实现，也便于求解，因此，研究传感器动态特性时最常用的输入信号函数就是阶跃信号函数和正弦信号函数。

采用阶跃信号作为输入信号研究传感器动态特性的方法，称为阶跃响应法，也叫时域的瞬态响应法；而采用正弦信号作为输入信号研究传感器的动态特性的方法，称为频率响应法。应用这两种方法可从时域和频域两方面来分析传感器的动态误差，给出其动态特性指标。

1）阶跃响应

给静止的传感器输入一个单位阶跃函数信号：

时，传感器的输出特性称为阶跃响应特性。

对于一阶传感器系统，其阶跃响应曲线近似为图1.28所示。

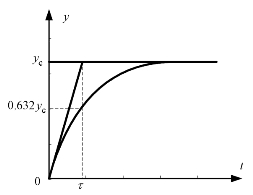
图1.28　一阶传感器系统的阶跃响应曲线

图1.28中，yc为一阶传感器系统在阶跃信号作用下，最后达到的稳态值。这里定义传感器输出值上升到稳态值yc的63.2%所需的时间为时间常数τ。对于一阶传感器系统，常用时间常数τ作为其响应特性指标。

对于二阶传感器系统，其阶跃响应曲线近似为图1.29所示。

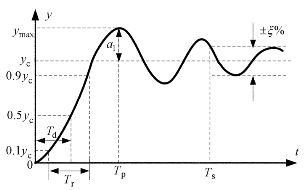
图1.29　二阶传感器系统的阶跃响应曲线

衡量二阶传感器系统阶跃响应特性的主要指标有：

·上升时间Tr——阶跃响应曲线由稳态值的10%上升到90%所需的时间。

·响应时间Ts——响应曲线衰减到与稳态值之差不超过±ξ%（如2%或5%）所需要的时间，也称为过渡过程时间。

·超调量a1——响应曲线第一次超过稳态值时的峰高，a1＝ymax－yc。超调量能说明传感器的相对稳定性。

·峰值时间Tp——响应曲线到达第一个峰值所需的时间。

·延滞时间Tj——响应曲线达到稳态值的50%所需的时间。

·衰减率ψ——相邻两个波峰高度下降的百分比，即(www.xing528.com)

·稳态误差ess——无限长时间后，稳态输出值与理想输出值的偏差δss的相对值，即

上述就是一阶和二阶传感器时域响应的主要指标，对于一个传感器，并非每一个指标都要给出，往往只要给出几个被认为是重要的性能指标就可以了。

了解传感器的动态特性指标，是为了在测量时避免严重的动态误差，下面举例说明。

【例1.8】　热电偶测量容器中液体温度过程中的动态误差分析。

热电偶在测量前置于环境温度之中，设环境温度为T0，被测液体的温度设为T，且T＞T0。测量时，把置于环境温度中的热电偶放于盛放液体的容器中，这时，热电偶的测量参数（输入量）发生突变，从T0上升到T，而热电偶的输出并不能立即从T0上升到T，而是有一个逐渐变化上升的过程。如图1.30所示，热电偶的温度从T0上升到T，经历了时间t0→t的过渡过程，如果不注意到这一过程，测温结果必定会产生很大的误差。图1.30中，测试曲线与阶跃波形的差值，就是动态误差。

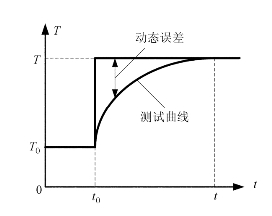
图1.30　热电偶测温过程

总的来说，动态误差一方面是因为激励信号的变化而产生的，另一方面是由于传感器测量电路、机械惯性、延时等原因而产生的。

2）频率响应

设输入信号为

输出为

频率响应特性是指：输入频率（ω）不同、幅值（X）相等的正弦信号x（ω），输出信号y（ω）的幅值Y和相位φ与输入频率ω之间的关系，即幅频特性与相频特性。

φ（ω）称为传感器的相频特性。对于传感器而言，由于其输出滞后于输入，所以相位角φ通常是负值。

由于相频特性与幅频特性之间有一定的内在关系，所以，研究传感器的频域特性时，主要用幅频特性。典型的对数幅频特性曲线如图1.31所示。

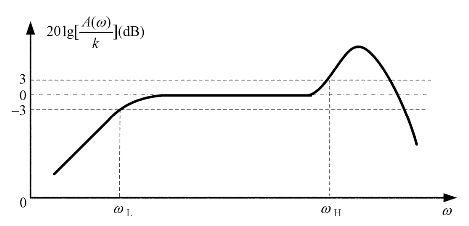
图1.31　典型的对数幅频特性曲线

图1.31中，0dB的水平线是理想的幅频特性，实际上是零阶系统的幅频特性。零阶传感器系统的频率响应函数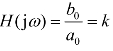，则其幅频特性A（ω）＝|H（jω）|＝k，纵坐标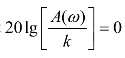（dB），因此，0dB的水平线是理想的零阶系统的幅频特性。在工程上，常将±3dB所对应的频率范围作为频率响应范围，又称通频带，它等于上截止频率ωH与下截止频率ωL的差值。通频带（ωH－ωL）是衡量传感器动态响应特性的重要指标之一。