传感器动态模型及其描述方式

动态模型是指传感器在动态信号作用下，其输出和输入信号的一种数学关系。动态模型通常采用微分方程和传递函数来描述。

1）微分方程

在研究传感器的动态响应特性时，一般都忽略传感器的非线性及随机变化等因素，而把传感器看成一个线性的定常系统来考虑，即用线性常系数微分方程来描述传感器输出量y（t）与输入量x（t）的动态关系，其通式为

这是一个n阶线性常系数微分方程，式中，a0、a1、…、an，b0、b1、…、bm是取决于传感器结构参数的常数。对于传感器，除b0≠0外，一般b1＝b2＝…＝bm＝0。

对于常见的传感器，其动态模型通常可用零阶、一阶或二阶的常微分方程来描述，分别称为零阶环节、一阶环节和二阶环节，其方程如下：

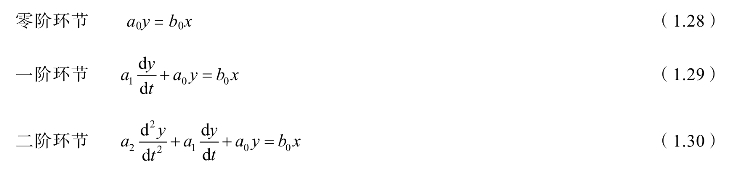
凡是能用一个零阶线性微分方程来描述的传感器就称为零阶传感器。依此类推，能用一阶、二阶线性微分方程来描述的传感器就称为一阶、二阶传感器。一般阶数越高，传感器的动态特性就越复杂。

零阶环节在测量上是个理想环节，即无论输入量x（t）随时间怎样变化，传感器的输出总是与输入成确定的比例关系，在时间上也无滞后，是一种与频率无关的环节，故又称为比例环节或无惯性环节。严格来讲，这种零阶传感器是不存在的，只有在一定工作范围内，某些高阶传感器系统可近似地看成是零阶环节。在实际中，经常遇到的是一阶和二阶环节的传感器。

【例1.7】　分析加速度传感器的动态特性。

如图1.24所示，将这样的加速度传感器与被测物连接在一起，用以测量被测物相对于地球参照物的加速度a，设被测物相对地球参照物的位移为x，则其加速度a可表示为。

图1.24　加速度传感器示意图

扫描下图可浏览AR资源——加速度传感器模型。

由于加速度传感器与被测物连接在一起，则可利用传感器质量块m相对于其外壳的位移y来反映外壳（被测物）相对于地球参照物的加速度a。

取质量块m为分析对象，它受弹簧力为-ky，受阻尼力为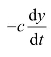，由牛顿第二定律知

这样，就可以用传递函数H（s）作为动态模型来描述传感器的动态响应特性。它具有这样一些特点：(www.xing528.com)

①传递函数H（s）反映的是传感器系统本身的特性，只与系统结构参数ai、bi有关，而与输入量x（t）无关。因此，用传递函数H（s）可以简单而恰当地描述传感器的输入-输出关系。

②对于传递函数H（s）描述的传感器系统，只要知道X（s）、Y（s）、H（s）三者中任意两者，就可方便地求出第三者。如图1.25所示，只要给系统一个激励信号x（t），便可得到系统的响应y（t），系统的特性就可被确定，而无须了解复杂系统的具体内容。

图1.25　传递函数框图

③同一个传递函数可能表征着两个完全不同的物理系统，说明它们具有相似的传递特性。但不同的物理系统有不同的系数量纲，即通过系数ai和bj（i＝0，1，…，n；j＝0，1，…，m）反映出来的。

④对于多环节串、并联组成的传感器系统，如各环节的阻抗匹配适当，可忽略相互之间的影响，则传感器的等效传递函数可按代数方式求解而得。

由n个环节串联而成的传感器系统，如图1.26所示，其等效传递函数为

图1.26　多环节串联的传感器系统

由n个环节并联而成的传感器系统，如图1.27所示，其等效传递函数为

图1.27　多环节并联的传感器系统

式中，Hi（s）为各环节的传递函数。

由此可见，对于多环节的传感器测量系统，用传递函数来描述其输入-输出关系，很容易看清各环节对系统的贡献，便于对测量系统进行改进。

⑤采用传递函数的另一个好处是，当传感器比较复杂或传感器的基本参数未知时，可通过实验求出传递函数。