每一台傅立叶变换红外光谱仪,由以下几部分构成:一个光源、一个干涉仪(分束器是它的一部分)以及一个检测器。其基本结构如图3-1-1所示。
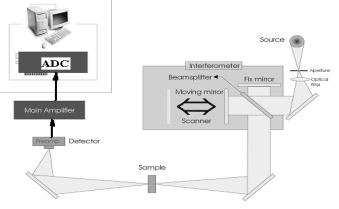
图3-1-1 傅立叶变换红外光谱仪原理结构
其中干涉仪是红外光谱仪的心脏,其基本原理结构如图3-1-2所示。

图3-1-2 干涉仪原理结构图
干涉仪由分束器、动镜以及固定镜和红外线光源组成。由于红外光源发出的红外光是连续的,每一种单色光都要发生干涉,使得红外干涉图是由多色光的干涉光组成的。我们可以通过以下分析傅里叶红外线光谱气体分析仪实际得到的光谱情况。
在干涉仪的出口,两束有光程差的光发生干涉,然后到样品。在最理想的情况下,先假设只有单色光的情况,我们假设分束器没有任何吸收,反射率和透射率各占一半。那么必然有一半的光透射过分束器到动镜,又从动镜反射回到分束器,另外一半反射到固定镜又从固定镜反射回到分束器,这两束光从离开分束器到重新到分束器,必然产生距离差,被称之为光程差。
当动镜移动距离为n/4 λ,即光程差为n/2 λ时,动镜距离如图3-1-3所示。
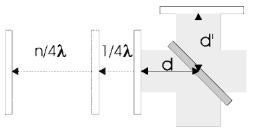
图3-1-3 动镜移动距离为n/4λ示意图
此时,由于两者的相位差正好等于半波长,两者的相位正好相反,此时发生干涉,两束光相加后相互抵消,光强正好为零,如图3-1-4所示,若此时进行检测,则检测到的信号为零。
同理,当动镜移动距离为n/2λ,即光程差为nλ或者光程差为0时,两者之间的相位相差正好等一个波长,也就是说达到最理想的状况,检测器检测到的光强和单色光源发出的光强完全相等。

图3-1-4 单色光在光程差为n/2λ时光强示意图
因为动镜以一定的速度(ν)移动,检测器上得到的信号是正弦波信号。最理想状态下的单色光通过理想干涉仪时所得到的干涉图与单色图的光强成正比关系。但实际上是不可能达到上述理想状态的,这主要是因为:即便是同一种物质(样气),不同波长的光反射率和折射率都不相同,在实际状况中根本不存在反射率和折射率各占50%的情况,也没有办法找到这种理想的分束器;另外从红外线仪器本身的性能来看,为了去掉红外线自身的电器噪音和其他干扰,通常都装有滤波电路,但这样就使得放大器的响应也与频率有关,从而使得基本不存在对所有波数都能有均匀响应的仪器。可以简单来说,需要考虑一个与波数有关的因子。其公式如下所示。其中
![]()
其中:
Bυ表示了波数υ光源经过仪器调制后(分束器效率、检测器和放大器的响应)的强度。
I'(δ) 光束强度(https://www.xing528.com)
Bυ 在波数υ光源经过仪器调制后(分束器效率、检测器和放大器的响应)的强度
υ 波数υ=1/λ
δ 光程差
由于单色光的干涉图是余弦波,进行cosine傅里叶逆变换非常简单,因此最终的我们所需要的红外线光谱是从上述干涉图进行cosine傅里叶逆变换计算得到。这也就是傅里叶变换光谱分析名称的来源。 在工程运用产品中,我们经常使用HeNe激光用来控制动镜的位置。其基本原理如图3-1-5所示。

图3-1-5 动镜位置调整示意图
在进一步的来看,实际上红外线光源所发出的应该是连续的辐射或者多色光,例如中红外的Globar光源或近红外的钨灯许多连续波数(即频率)的光同时发射,此时所得的干涉图要复杂得多。检测器检测得到的干涉图是每一个波数的干涉图的矢量和。图3-1-6分别给出了2种波(a)、3种波(b)和4种波(c)相互叠加以后产生的干涉示范。
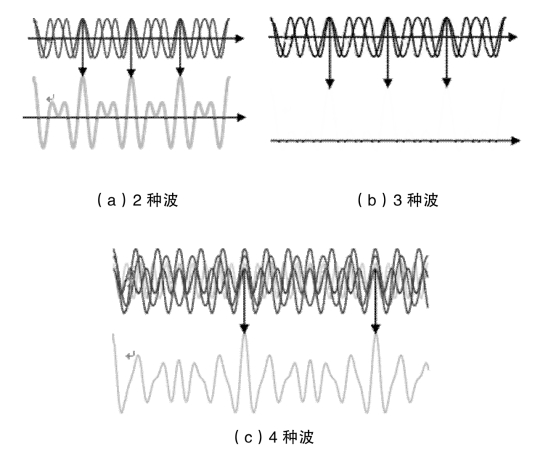
图3-1-6 多个波叠加示范
对于连续光源,干涉图用积分表示,可表示为:

从上面公式可以看出理论上,我们可以从-∞到+∞范围,得到一张完整谱图,而且可以任何分辨率。但这同时也就意味必须做到:
动镜的移动距离可以无限远;
数据采样间隔无限小。
如果要做到“动镜的移动距离可以无限远”,这就意味着干涉仪要有无限长,这是不可能的。“数据采样间隔无限小”就意味着光程间隔无限小,也就是数据采集点时间间隔为无限小,也就是意味着“无尽”的计算机内存消耗以及“无限”时长的傅里叶变换计算时间,这显然也是不可能的,从这点来看,在实际工程中得到的干涉图实际上已经存在了存“理论误差”。然后我们需要在干涉图的基础上进行傅里叶逆变换,得到如下公式:
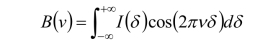
换一个角度来看,不同的谱图范围的选择,决定了仪器采用的光学组件,如图3-1-7所示。而在红外线光谱分析领域中,不管采用的是哪种光学组件,其基本原理都应该是相同的。

图3-1-7 光谱和光学组件关系示意图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




