风险分析方法之概率树

概率是度量某一事件发生的可能性大小的量，它是随机事件的函数。必然发生的事件，其概率为1，不可能事件，其概率为0，一般的随机事件，其概率在0 和1 之间。

某事件的概率可分为主观概率和客观概率两类。通常把以人为预测和估计为基础的概率称为主观概率，如产量、销售单价、建设投资、建设工期等。以客观统计数据为基础的概率称为客观概率，如水位、流量等。经济评价的概率分析主要是主观概率分析。

概率树分析是常用的风险分析方法之一，它是利用概率来研究和预测不确定因素对项目经济评价指标影响的一种定量分析方法。

概率树分析是假定风险变量之间是相互独立的，在构造概率树的基础上，将每个风险变量的各种状态取值组合计算，分别计算每种组合状态下的评价指标值及相应的概率，得到评价指标的概率分布，并统计出评价指标高于基准值的累计概率，从而判断项目的风险。

简单的概率分析是在根据经验设定各种情况发生的可能性（概率）后，计算项目净现值、项目净现值的期望值及净现值大于等于零时的累计概率。一般的计算步骤如下。

（1）通过敏感性分析，确定项目的主要不确定因素（风险因素）。

（2）判断各不确定因素（风险因素）可能发生的情况。

（3）确定每种情况可能发生的概率，每种情况发生的概率之和必须等于1。

（4）求出各可能发生事件的净现值、加权净现值，然后求出净现值的期望值。

（5）求出净现值大于等于零的累计概率。

风险评价的判别标准：财务（经济）净现值大于等于零的累计概率值越大，风险越小。

以下先来介绍项目净现值的期望值，然后举例说明概率树分析法。

期望值是用来描述随机变量的一个主要参数。

所谓随机变量就是这样的一类变量，我们能够知道它的所有可能的取值范围，也知道它取各种值的可能性，但却不能肯定最后它的确切的取值。比如说有一个变量X，知道它的取值范围是0、1、2，也知道X 取值0、1、2 的可能性分别是0.3、0.5 和0.2，但是究竟X 取什么值却不知道，那么X 就称为随机变量。从随机变量的概念上来理解，可以说在投资项目经济评价中所遇到的大多数变量因素，如投资额、经营成本、产品价格、项目寿命期等，都属于随机变量的范畴，因而主要根据它们计算出来的经济评价指标也都是随机变量，所以项目净现值也是一个随机变量。

期望值是反映随机变量取值的平均值。但这个平均值绝不是一般意义上的算术平均值，而是以随机变量各种取值的概率为权重的加权平均值，如前面所谈到的随机变量X，它的期望值就不是1，而是0×0.3＋1×0.5＋2×0.2＝0.9。

一般来讲，期望值的计算式可表达为：

式中：E（X）为随机变量X 的期望值；xi 为随机变量X 的各种取值；pi 为X 取值xj 时所对应的概率值。

根据期望值的计算式 （2-49），可以很容易地推导出项目净现值的期望值的计算式如下：

式中：E（NPV）为净现值的期望值；NPV i 为每种情况下的净现值；P i 为每种情况可能发生的概率值；NPV iP i 为每种情况下的加权净现值。

由式（2-50）可知，将各种情况可能发生的概率分别与其对应的净现值相乘，得出加权净现值；将各种情况下的加权净现值相加，即为期望净现值。期望净现值表示项目净现值以概率为权重的加权平均值，是项目净现值最可能的取值。

【例2-24】 已知某投资方案各种不确定因素可能出现的数值及对应的概率见表2-6。假定投资发生在期初，各年净现金流量均发生在期末，标准折现率为10%，试用概率法判断项目的可行性及风险情况。

表2-6　某投资项目数据

解：（1）绘出决策树图（图2-18）。

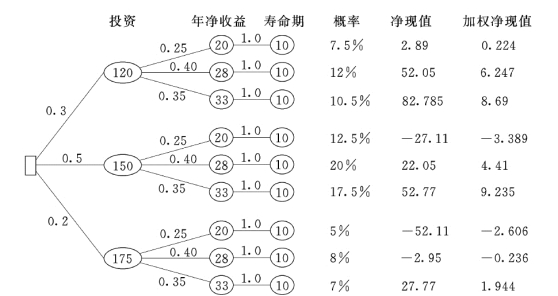
图2-18　某投资方案决策树图

（2）计算各种可能发生情况下的项目净现值及其概率。(www.xing528.com)

1）投资120 万元，年净收益有三种情况。

第一情况：投资120 万元，年净收益20 万元，则此种情况下的净现值为：

FNPV ＝－120 ＋20（P/A，10%，10）＝2.89（万元）

可能发生的概率为：0.3×0.25＝0.075＝7.5%

加权净现值为：2.98×0.075＝0.224（万元）

第二种情况：投资120 万元，年净收益28 万元，则此种情况下的净现值为：

FNPV ＝－120 ＋28（P/A，10%，10）＝52.06（万元）

可能发生的概率为：0.3×0.4＝0.12＝12%

加权净现值为：52.06×0.12＝6.247（万元）

第三种情况：投资120 万元，年净收益33 万元，则此种情况下的净现值为：

PNPV ＝－120 ＋33（P/A，10%，10）＝82.785（万元）

可能发生的概率为：0.3×0.35＝0.105＝10.5%

加权净现值为：82.785×0.105＝8.69（万元）

2）投资150 万元和投资175 万元同理分析计算。

（3）计算期望净现值。

将各种情况下的加权净现值相加即得：

期望净现值＝0.224＋6.247＋8.69－3.389＋4.41＋9.235－2.606－0.236＋1.944

＝24.52（万元）

（4）列出净现值小于零的累计概率表（表2-7），计算净现值大于等于零的累计概率。

由表2-7 可得：

净现值小于零的累计概率：

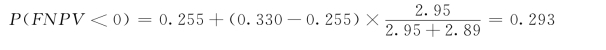
净现值大于等于零的累计概率为：

P（FNPV ≥0）＝1－P（净现值小于零）

＝1－0.293

＝0.707

由此可知，项目期望净现值为24.51 万元，各种情况项目净现值大于等于零的累计概率是70.7%，说明项目风险较小，项目可行。

表2-7　净现值累计概率