资金等值计算的基本公式解析

工程经济评价中，通常考虑资金的时间价值，把在某一个时间点发生的资金额转换成另一个时间点的与其等值的资金额，这样的一个转换过程就称为资金的等值计算。

由于利息是资金时间价值的主要表现形式，所以资金等值计算的方法与用复利法计算利息的方法完全相同。根据支付方式和等值换算点的不同，资金等值计算公式可分为3类：一次支付类型、等额支付类型和等差支付类型。

（一） 一次支付类型

一次支付又称整付，是指所分析的系统的现金流量，无论是流入还是流出均在某一个时间点上一次发生。它包括两个计算公式。

1.一次支付终值公式

如果有一笔资金，按年利率i 进行投资，n 年后的本利和应该是多少？这就是已知现值（P）、计息次数（n）、折现率（i），求终值（F）的问题，解决此类问题的计算公式称为一次支付终值公式，其形式是：

在式（2-10）中，（1 ＋i）n 称为复利终值系数，记为（F/P，i，n）。因此，式 （2-10）又可写成如下形式：

在实际应用中，为了计算方便，按照不同的利率i 和计息次数n，分别计算出（1＋i）n的值（终值系数），排列成一个表，称为终值系数表。在计算时，根据i 和n 的值，查表得出终值系数后与P 相乘即可求出F 的值。

式 （2-10）表示在利率为i，计息次数为n 的条件下，终值和现值之间的等值关系。一次支付终值公式现金流量图如图2-3 所示。

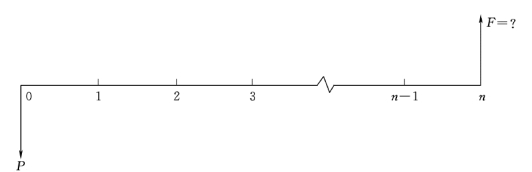
图2-3　一次支付终值公式现金流量图

【例2-7】 某公司向银行贷款50 万元，年利率为11%，复利计息，贷款期限为2年，到第2 年末一次还清，到期应偿还本利和为多少？

解：这是一个已知现值求终值的问题。

已知：P ＝50 万元，i＝11%，n＝2，由式（2-10）可得：

即2 年后公司需向银行一次性偿还本利和61.605 万元。

这个问题也可以查表计算求解。由复利系数表（见附录）可查得：

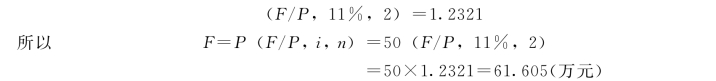
2.一次支付现值公式

如果希望在n 年后得到一笔资金F，在年利率为i 的情况下，计算现在应该投资多少？即已知F、n、i，求现值P。解决这类问题用一次支付现值公式，其形式为：

在式（2-11）中，（1 ＋i）－n 称为复利现值系数，记为（P/F，i，n）。因此，式 （2-11）又可以写为：

一次支付现值公式现金流量图如图2-4 所示。

【例2-8】 某公司拟两年后从银行取出50 万元，银行存款利率为年息8%，复利计息，现应存入多少钱？

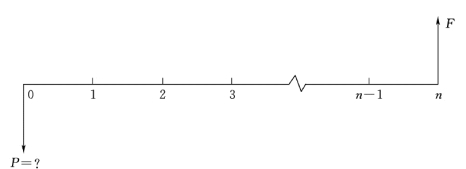
图2-4　一次支付现值公式现金流量图

解：这是一个已知终值求现值的问题，根据式（2-11）可得：

即现在应存入银行42.867 万元。

或通过查表得现值系数：

算得

（二） 等额支付类型

等额支付是指所分析的系统中，现金流入与现金流出不是集中在某一个时间点，而是在连续的多个时间点上发生，形成一个现金流序列，并且在这个序列的现金流量数额大小是相等的。它包括4 个基本公式。

1.等额年金终值公式

在年利率为i 的情况下，连续从第一年到第n 年每年年末支付一笔等额的资金A，求n 年后由各年资金的本利和累计而成的总值F，即已知A、i、n，求F。其现金流量图如图2-5 所示。

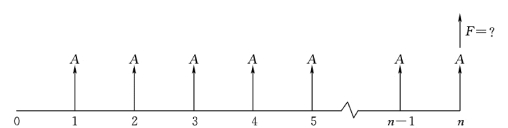
图2-5　等额年金终值公式现金流量图

其计算公式为：

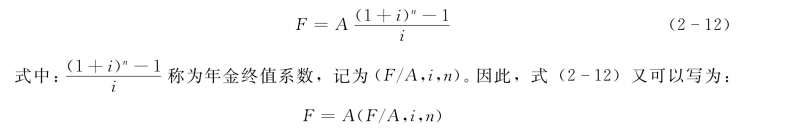
【例2-9】 某企业为设立技术改造基金，从第1 年至第5 年，每年存入银行10 万元，存款年利率为9%，复利计息，问第5 年末该基金内有多少钱？

解：这是已知年金求终值的问题，根据式（2-12）可知：

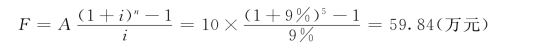
或查复利系数表得年金终值系数计算得：

2.等额年金现值公式

等额年金现值公式的含义是：在n 年内每年等额收支一笔资金A，在利率为i 的情况下，求此等额年金收支的现值总和，即已知A、i、n 求P。其现金流量图如图2-6 所示。

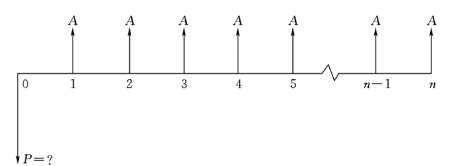
图2-6　等额年金现值公式现金流量图

将等额年金终值式（2-12），代入一次支付现值式（2-11）：

得等额年金现值公式：

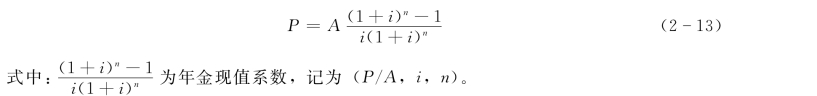
式 （2-13）又可写为：

【例2-10】 某企业拟5 年内每年需要投入资金100 万元用于技术改造，企业准备存入一笔钱以设立基金，提供每年技术改造所需用的资金。已知年利率为6%，复利计息，问企业现在应存入基金多少钱？

解：这是一个已知年金求现值的问题，根据式（2-13）可得：

(www.xing528.com)

或查复利系数表得年金现值系数求解：

3.偿债基金公式

偿债基金公式的含义是：为了筹集n 年后所需的一笔资金，在利率为i 的情况下，求每个计息期末应等额存储的金额。即已知F、i、n 求A。其现金流量图如图2-7 所示。

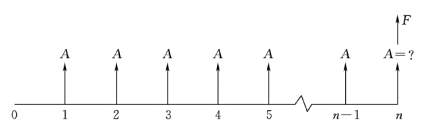
图2-7　偿债基金公式现金流量图

其计算公式由等额年金终值式（2-12）推导得出：

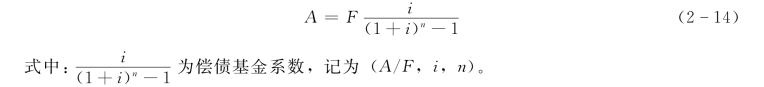
式 （2-14）又可写为：

【例2-11】 某企业5 年后需要一笔20 万元的资金用于固定资产的更新改造，如果年利率为8%，问从现在起该企业每年末应存入银行多少钱？

解：这是一个已知终值求年金的问题，根据式（2-14）有：

或

4.等额资金回收公式

等额资金回收公式的含义是：期初一次投资数额为P，欲在n 年内将投资全部收回，则在利率为i 的情况下，求每年应等额回收的资金。这就是已知P、i、n 求A。其现金流量图如图2-8 所示。

图2-8　等额资金回收公式现金流量图

其计算公式可根据偿债基金公式和一次支付终值公式推导出。即：

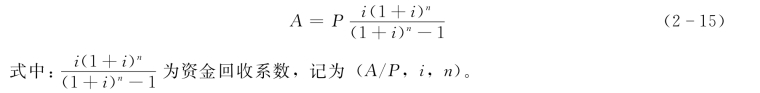
因此，等额资金回收式（2-15）又可写为：

【例2-12】 某项目期初以年利率14%投资10 万元，拟计划3 年内等额回收全部投资复利本利和，每年可回收的资金为多少？

解：这是一个已知现值求年金的问题，根据式（2-15）有：

或

（三） 等差支付类型

等差支付是逐期作等额递增（减）的现金流系列。等差系列的复利等值变换，主要是将等差化为等额系列资金。

如图2-9 所示，现金流为逐期递增的现金流，第一期末无资金发生，从第二期开始资金金额依次为G，2G，3G，…，至第n 期末为（n－1）G。

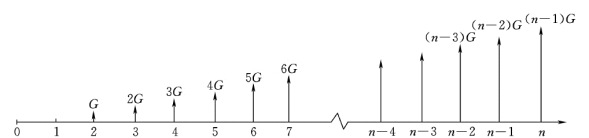
图2-9　等额递增的现金流量图

（1）等差系列等值的复利终值F。依据一次收付复利法的终值变换，在第n 期的终值F 等于在每一个期末的现金流的终值总和。

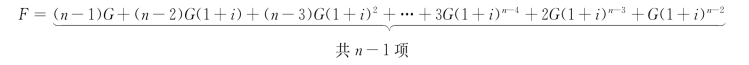
改变上式的系数，重新组成如下的序列：

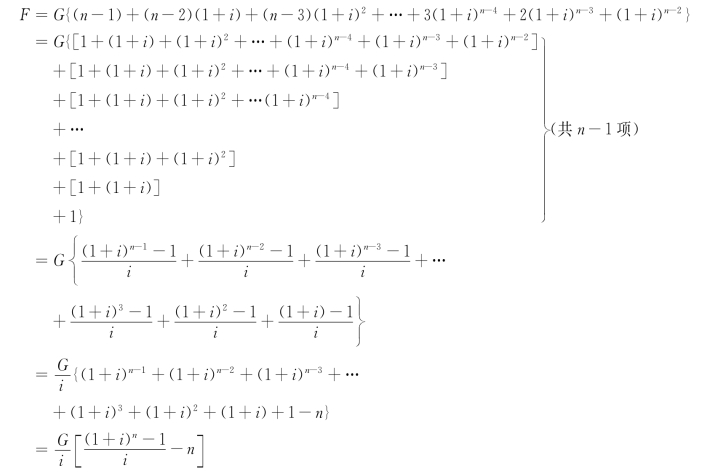
得等差系列的复利终值公式：

（2）等差系列的复利现值公式。依据一次支付现值式（2-11）：

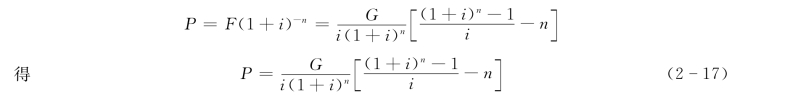
（3）与等差系列等值的等额年金A。依据等额偿债基金式（2-14）：

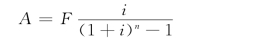
将式（2-16）代入式（2-14）：

【例2-13】 某企业设备年使用费为70 万元，考虑作技术改造，需于第一年投资和使用费用为50 万元，而后每年递增5 万元，如果设备寿命周期为10 年，年利率i＝10%，问该企业是否应对这一设备作技术改造？

解：根据题意，作技术改造后的现金流量图如图2-10 所示。

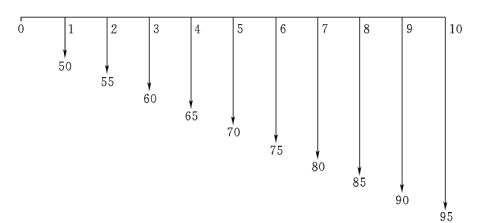
图2-10　作技术改造后的现金流量图 （单位：万元）

求出与技术改造全部费用等值的年值A。图2-10 所示现金流量图可分解为两个现金流量图，如图2-11 和图2-12 所示。

图2-11　分解后的现金流量图1 （单元：万元）

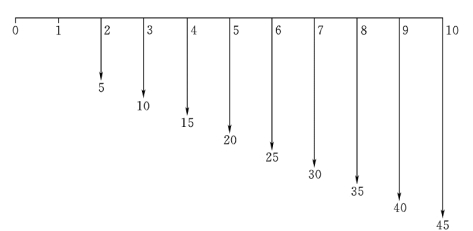
图2-12　分解后的现金流量图2 （单元：万元）

由图2-11 所示现金流量图得：

由图2-12 所示现金流量图得：

与技术改造全部费用等值的年值：

可见，与原设备每年使用费用70 万元相比，作技术改造较为经济。